1.1.3 Избор на бройна система за реализация на цифрови изчислителни устройства

Choice notation system of implementation in digital processors

Методи и модели за количествена оценка на информацията

В днешни дни най-популярните способи за измерване на информацията са:

· Обемен (азбучен);

· Ентропиен ;

· Алгоритмичен .

Обемният способ за измерване на информацията е най-простият и грубият. Съответната количествена оценка на информациятасе нарича обем. Например, обем на информацията в едно съобщение е броят на символите в съобщението.

Тъй като едно и също число може да бъде записано по много и различни начина (в зависимост от използваните символни азбуки), този начин е чувствителен, нееднозначен спрямо представянето (записа) на самото съобщение.

Ентропийният способ за количествена оценка на информацията е най-прилаганият в областта на информационната теория и теорията на кодирането. Този способ се основава на следния модел: информацията, съдържаща се в дадено съобщение, може нестрого да се третира в смисъла на нейната новост, или казано по друг начин, да се третира като начин за намаляване на неопределеността на знанията за обекта.

Подходът към информацията като мярка за намаляване на неопределеността на знанията позволява тя да бъде измерена количествено, което се оказва извънредно важно за информатиката в цяло. По тази причина ще разгледаме по-подробно въпросите, свързани с определянето на количеството информация, използвайки няколко примера.

Нека имаме монета, която подхвърляме върху равна повърхност. В статистически смисъл имаме две събития, които се реализират с еднаква вероятност – монетата е в състояние “ези” или е в състояние “тур”. Твърди се, че еднаквата вероятност се постига във все по-силна степен, когато броят на опитите клони към безкрайност.

Преди поредното хвърляне на монетата съществъва неопределеност в нашето познание (съществуват две възможности за реализация), поради което не е възможно категорично да се предскаже реалното положение на монетата (ези или тур) Пълната определеност на това събитие настъпва след хвърлянето, тъй като ние виждаме (получаваме зрително съобщение) за положението на монетата. Това съобщение води до намаляване на неопределността на нашите знания два пъти. Направената оценка следва от факта, че преди хвърлянето са налични две вероятни събития, а след хвърлянето – само едно, т.е. два пъти по-малко.

В действителност съществуват и други подобни ситуации – например хвърляне на игрално зарче, за което има 6 възможни състояния (равно вероятни събития).

Може да обобщим, че колкото повече са възможните крайни състояния на обекта, толкова повече е началната неопределеност и съответно толкова повече информация ще съдържа съобщението за реализираното състояние.

Нека за изпращане на съобщение разполагаме с m на брой символа (разбирай брой на възможни състояния). Тогава количеството (броят) N на различните възможни съобщения, съдържащи I на брой символа ще бъде

Тогава количеството информация се определя така (формула на Ралф Хартли за равновероятни съобщения, предложена през 1928 год.)

Тук ще припомним даденото по-горе определение за обемния способ за измерване на количеството информация в едно съобщение, според което количеството се измерва с броя на символите в него.

Ако в азбуката за съобщения има само 2 символа (m=2), т.е. става дума за двоични съобщения (двоични комбинации). Тогава получаваме формулата

Забележително е какво е единица количество информация? Това е случаят, когато имаме 2 възможни събития, т.е.

Дименсията за количество информация се нарича bit (binary digit). Въведена е от К. Шенон.

Ако цифровото съобщение е написано с десетични цифри, в определението се използва десетичен логаритъм. Тогава количеството информация се обозначава с дименсия dit (decimal digit). Въведена е от Хартли. Между двете дименсии се установява следната зависимост

Така може да се оцени, че количеството информация, което се съдържа в един dit е 3,32193 пъти повече от това, изразено с един bit.

Горните константи позволяват да се отговори на следния въпрос: колко двоични символа са необходими за едно двоично съобщение, ако изходният текст на съобщението е записан, например, с 56 десетични цифри? Отговорът е чрез формулата

Или с други думи, 1[dit]=3,32193 [bit], т.е. една десетична цифра съдържа колечество информация, което се измерва с 3,32193 двоични цифри. И тъй като оценката с реално число е невъзможна, то двоичните цифри са 4, което пък води до определен излишък, който пък може да се използва по различен начин, както ще бъде пояснено по-късно в тази книга.

Съществуват разбира се и ситуации, в които възможните събития могат да имат различни вероятности за реализация. Тогава формулата за изчисляване на количеството информация в случай на разновероятни събития е предложена от Клод Шенон в 1948 год.

където с I е означено количеството информация; с N – броят на възможните събития; с p_i – вероятността на i-тото събитие.

ПРИМЕР: Нека хвърляме 4-ри стенна пирамида. Събитията тя да се окаже легнала на всяка отделна стена са 4 на брой и са оценени както следва: p1=1/2, p2=1/4, p3=1/8, p4=1/8.

Тогава количеството информация, което ще получим след реализацията на поредното събитие според (1.1.3.7) ще се изчисли така

Като имаме предвид формулата

за израза на примера получаваме

Ако в разгледаният пример се наложи изискването пирамидата да бъде равностранна, то тогава вероятностите на отделните събития ще бъдат еднакви. Изчислението на количеството информация ще доведе до оценка 2 [bit], което индуцира твърдението, че количеството информация достига своя максимум, когато отделните събития са равновероятни.

С това беше илюстриран ентропийният (вероятностният) подход за определяне количеството информация в едно съобщение. При това бяха въведени нови понятия, които ще ни се наложи да използваме в бъдеще.

Третият способ за измерване на количеството информация беше наречен алгоритмичен. Основанията за този способ се изясняват чрез следните разсъждения.

Всеки би се съгласил с твърдението, че последователността 0101...01 е по-сложна от 0000...00. Още по-сложна от предидущите последователности е последователността, в която цифрите 0 и 1 се редуват случайно (както при хвърляне на монета). Следователно, програмите, генериращи такива последователности, също биха се различавали в своята сложност.

Изложените разсъждения позволяват да се предположи, че на всяко съобщение може да се припише някаква количествена характеристика, която да отразява сложността на една програма, която генерира това съобщение.

Коя бройна система е за предпочитане?

Представеният по-горе апарат ще трябва да ни помогне, за да си отговорим на поставения въпрос. В крайна сметка ние преследваме техническата реализация на средствата за преработка на информацията, ето защо никак не може да ни бъде безразлично как това ще бъде постигнато, като се има предвид огромното количество информация или още – огромната сложност на нейната преработката.

Въпреки казаното в предходните раздели, двузначната система често е подлагана на съмнения и проверка. Въпросът е в това, дали нейното използване следва да бъде предпочетено и въз основа на какви обективни оценки може да се направи такъв избор. Това е въпросът, който ще бъде дискутиран тук по-долу.

Когато става дума за реализация на изчислителни устройства, най-често се използват два критерия – оценка на обема апаратни разходи, които са направени за тяхната реализация и оценка за бързодействието на тяхното функциониране. За да се оцени как ще се влияят апаратурните разходи от основата q на бройната система, избрана за представяне (кодиране), се построява оценъчна функция. За целта се изхожда от обема на входно-изходното множество понятия, т.е. от общия брой N различни обекти (разбирайте всички видове конкретни данни), необходими да бъдат представяни в дадено изчислително устройство. Дължината на кодовата дума от n на брой q-ични позиции, необходима за еднозначно представяне на елементите на множеството, се определя от неравенството

Kато се има предвид, че бройната система е позиционна, то числото N може да се представи чрез максималното изобразимо число в поле с дължина n разряда

както следва:

При тези положения апаратните разходи са пропорционални на броя на реализираните позиции, а апаратните разходи за реализирането на една позиция са пропорционални от своя страна на основата на бройната система. Тогава апаратните разходи за реализация на изчислителното устройство могат да се оценят с функцията

За сравнение на тези разходи, с разходите при използване примерно на двоична бройна система, се образува друга оценъчна функция, имаща вида:

Тази функция ще покаже колко пъти в повече са апаратните разходи при реализация на бройна система с основа q, спрямо тези при използване на двоична бройна система. Полученият израз има вида:

Изследването на крайния израз за оценъчната функция F(q) има смисъл за q>1. Mоже да се покаже (което не е направено тук), че функцията, разгледана като непрекъсната, има за минимум константата

q = e = 2,718281828459045 … .

Твърдението ще докажем по следния класически начин – разглеждаме като отношение последния вид на функцията F(q), получен в горния израз (1.1.3.6) така:

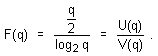
Диференцираме този вид на функцията F спрямо аргумента q според следната обща таблична формула:

След това за да намерим положението на екстремума на оценъчната функция F по оста на аргумента q, трябва да решим уравнението:

И така, за производната се получава следното:

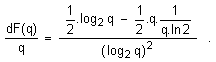
Този вид се получава като се използват две общи формули. Първата се отнася до табличната производна на общ логаритъм, имаща вида:

по силата на която формула имаме следната производна:

Освен това, тъй като в израза за производната на функцията F се срещат логаритми при различни основи, то се налага да привеждането им към една и съща основа, което се постига въз основа на следната (втора) обща формула:

Така замествайки конкретните изрази за общите формули, в израза за производната на функцията F получаваме:

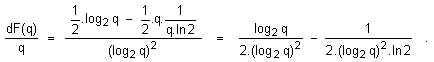
Приравнявайки току що получения израз на нула и след естествено следващите в полученото уравнение съкращения, се стига до уравнението:

от което произтича и окончателното решение q=e. Това окончателно решение доказва по-горе изказаното твърдение, че най-икономична в смисъла на критерия (1.1.3.14) е бройната система с основа Неперовото число е.

По очевидни причини обаче, по-интересни са стойностите на оценъчната функция функция, посочени в таблица 1.1.3.9., изчислени за цели стойности на основата на бройната система q.

Таблица 1.1.3.1 Дискретни стойности на функцията

q	2	3	4	5	6	7	8	9	10
F(q)	1,0	0,946	1,0	1,078	1,148	1,247	1,333	1,42	1,505

От тази таблица се налага изводът, че в смисъла на формулирания за оценка на апаратните разходи критерий (1.1.3.14), най-изгодна е троичната бройна система. Приложението на този извод обаче е ограничено по силата на предположението, че апаратните разходи за реализацията на един q-ичен разряд са пропорционални и на основата на бройната система. Ето защо практическо приложение са намерили най-вече двоичната бройна система и нейните производни – осмична и шестнадесетична.

Оценка за влиянието на избраната бройна система върху другата характеристика на изчислителното устройство – неговото бързодействие, може да се получи при много по-силни предпоставящи ограничения. Така например, за натурални позиционни бройни системи, основа за получаване на такава оценка може да бъде някоя типична, често изпълняваща се операция, като например умножение.

Известно е, че операцията умножение по същество представлява повтарящ се процес от формиране на поразрядните произведения и тяхното натрупване в междинната сума. Натрупванията са толкова, колкото са цифрите на числото, с което се умножава, т.е. максимум n, според израза (1.1.3.1). Формирането на поразрядното произведение също представлява процес на натрупване - умножаваното число се натрупва толкова пъти, колкото е елементарното количество на поредната цифра от множителя, а тя в дадената бройна система има максимална стойност (q-1). При тези означения максималният брой операции събиране при получаване на произведението ще се изрази както следва:

Оценъчната функция в този смисъл се построява аналогично на (1.1.3.13), т. е.

Стойностите на тази функция за цели стойности на аргумента са представени в следващата таблица.

Таблица 1.1.3.2 Дискретни стойности на функцията

q	2	3	4	5	6	7	8	9	10
S(q)	1,0	1,262	1,5	1,725	1,913	2,138	2,333	2,524	2,709

Явно се вижда преимуществото на двоичната бройна система, колкото и условна да е тази оценка.

В подкрепа на двоичната бройна система в смисъла на критерия бързодействие могат да се изтъкнат още следните мотиви:

· Скоростта за изпълнение на аритметическите операции в голяма степен зависи от времето за разпространение на последователните преноси в суматорите. В същото време суматорите, работещи в бройни системи с големи основи, са по-сложни и в тях се извършват много повече превключвания на разряд, поради което разпространението на преносите става много по-бавно по сравнение с това в двоичните суматори, чийто синтез и изследване е представено в книга [2];

· Апаратните методи за ускоряване на операция умножение, деление и елементарни математически функции постигат максимален ефект в двоична бройна система. Това се дължи на факта, че броят наличните незначещи цифри (нули) в двоичните съмножители е относително най-голям в сравнение с еквивалентите им в други бройни системи;

· Двоичната бройна система предлага удобна имитация за изпълнение на операции умножение и деление чрез изместване в ляво и в дясно за много и често срещани константи, кратни на 2.

В заключение може да се отбележи, че върху избора на бройната система, в която ще се провеждат определени изчисления, влияят още много други фактори, като например физическият принцип за реализация на устройството (имаме предвид казаното в началото на § 1.1), технологията на производство на неговите градивни елементи, алгоритмите за решаване на потребителските задачи и др. Въпреки това към настоящия момент двоичната бройна система няма конкурент.

Следващият раздел е:

1.1.4 Представяне на логическите данни (Presentation of logical data)