1.1.4 Представяне на логическите данни
Presentation of logical data
Логическите данни представляват
логическите константи "лъжа"
и "истина" и
тъй като са само две, те се кодират с двоичните цифри 0º”лъжа”, 1º”истина”. В случаите, когато
полето, в което се представят данните, е многоразрядно, каквото е например
разрядното поле на цифровите процесори, логическите константи се представят
чрез запълване на полето с една и съща двоична цифра: 00...0=”лъжа” или
11...1=”истина”. Логическите данни се декларират в езиците за програмиране от
високо ниво с ключовата дума за тип bolean, която определя и формàта (дължината)
на полето за представянето им на един байт (8 [b]).
Изложеното тук по-долу и в последствие предполага, че читателят е запознат с алгебрата на логиката, логическите елементи, синтеза на логически функции и теорията на крайните автомати.
Изчислителните устройства оперират с логическите данни като изпълняват известните логически операции:
- логическо отрицание НЕ
, (NOT) , notX
, ![]() ;
;
- логическо събиране (дизюнкция)
ИЛИ , (OR) , ![]() ;
;
- логическо умножение (конюнкция)
И , (AND) , ![]() ;
;
- логическа нееквивалентност
(NEQ) , ![]() , Mod2(X,Y) ;
, Mod2(X,Y) ;
- логическа еквивалентност (EQ) , ![]() .
.
Операция EQ обикновено се реализира без фиксиране на резултата. В повечето реални машинни реализации операцията се използва за формиране на признаците на резултата, т.е. като тест. С признаците на резултата, техния смисъл, формиране и актуалност читателят ще бъде запознат в глава 3 на тази книга.
Следващите операции:
- щрих на Шефер (NOR) , ![]() ;
;
- стрелка на Пирс (NAND) , ![]()
и други елементарни логически
операции от функционално пълното множество логически функции от два аргумента,
в чист вид не се реализират. Читателят лесно може да се досети, че те могат да
се изпълнят в комбинация от реализираните.
Непосредствено реализираните в цифровите
процесори логически операции обикновено са малко на брой. Те нямат решаваща роля
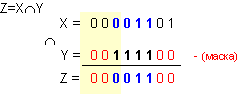
и могат да се приемат за помощни. Например операция логическо умножение
се използва най-често за маскиране (прикриване, скриване, не
пропускане) на отделни части от разрядната мрежа. Маскирането, като похват
за отделяне на части от данновите единици (порции), е често възникваща
алгоритмична потребност. Изпълнението на тези операции в
аритметично-логическото устройство е поразрядно (самостоятелно за
всеки бит на разрядната мрежа по отделно). Поразрядно означава, че резултатът
във всеки отделен разряд зависи единствено от стойностите в съответните разряди
на операндите. Например:
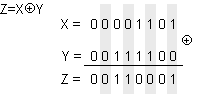
В програмирането на асемблерен език много често логическата операция NEQ от еднакви операнди (XÅX) се
използва за нулиране на съдържанието на даден регистър, което илюстрира
следващия пример
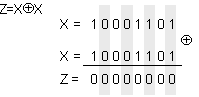
Резултатите се получават в многофункционалната логическа схема на
основния суматор, който се настройва според необходимата операция. Синтезът и
функционирането на този вид суматор и неговата принципна логическа схема са
изяснени в книга [2].
В резултат на логическите операции се
получават нови логически стойности или стойности, които потребителят желае да
интерпретира по свой собствен начин. Същото се отнася и до формираните признаци
на резултата, за които по-късно в тази книга отново ще се говори. За тези
ефекти на логическите операции читателят може да прочете още в книга [4].
Следващият раздел е:
1.1.5 Представяне на
символните данни (Presentation of character data)