1.1.5 Представяне на символните данни. Unicode

Character Data Representation. Unicode

За представяне на информацията човек използва развита система от абстрактни писмени знаци т.е. техни изображения (символи). В общия случай писмените знаци се определят като глифи. Глиф е общо наименование на всяко конкретно изображение от дадена писмена система. Абстрактното понятие за изображение се нарича графема. Глифи, които изобразяват една и съща графема, се наричат алографи.

Зад всеки символ (изображение) стои точно определен смисъл – буква, цифра, препинателен знак, математически символи и др. В случая е особено съществено да поясним, че компютърът (в най-разнообразните му форми) изобразява информацията визуално на дисплей, т.е. тя се възприема зрително. Изображенията на текстовите символи, както вече беше определено, се наричат глифи и техният брой, който използваме към настоящия момент, е огромен. Очевидно, при това положение, за представяне на множеството символи (глифи) следва да се построи подходяща кодова таблица. Историята на създаването на символните кодове е достатъчно дълга и по тази причина тя излиза от рамките на нашето внимание и цели, които преследваме тук. Ще представим само най-съществените факти, като нейното задълбочено изучаване оставяме на любознателния читател.

Кодът на символите естествено е двоичен, по причини, които вече бяха изяснени в §1.1. Кодовите таблици за множеството символи, които искаме да използваме, са добре известни, тъй като са определени с международни стандарти, като например:

ISO-7 (КОИ-7) – 7-битов код, който стандартизира символната азбука на системи за телеобработка, предаване на данни по съобщителни канали и за нанасяне на данни върху перфолента;

ISO-8 (КОИ-8) – 8-битов код, който стандартизира символната азбука на изчислителните системи за връзка с периферни устройства;

EBCDIC (ДКОИ) – 8-битов код, стандартизиран от фирмата IBM като код за използване в изчислителните системи;

ASCII (American Standart Code for Information Interchange) – 6, 7 или 8-битов код, стандартизиран през 1963 г. най-общо като код за обмяна на информация.

Стандартизираното множество от символи, чийто минимален обем е сведен до 256 символа, се дели най-общо на две части – подмножество графични символи (видими) и подмножество управляващи (служебни и невидими) символи. Като пример по-долу е пояснено как е изградена ASCII кодовата таблица. Кодът на символите представлява 8-разрядна двоична комбинация. Първата половина от всички възможни комбинации - 0xxx xxxx (007F) се съдържа в първата страница на кодовата таблица. Тук е основното множество символи (128 на брой) – управляващи, латински букви, десетични цифри, символи за математически операции и др. Окончателният състав и подредба на символите в първата страница (като 7-битов код) е приет като стандарт през 1967 г. Двоичната кодова комбинация на отделните графеми често се използва в алгоритмите в качеството си на число, ето защо в представените по-долу таблици са включени колонки с числовата им интерпретация в 10-чна и в 16-чна бройна система.

Първа страница на ASCII - таблицата

10-чен код	16-чен код	Символ	10-чен код	16-чен код	Символ	10-чен код	16-чен код	Символ	10-чен код	16-чен код	Символ
000	00	NUL	032	20	space	064	40	@	096	60	`
001	01	SOH	033	21	!	065	41	A	097	61	a
002	02	STX	034	22	“	066	42	B	098	62	b
003	03	ETX	035	23	#	067	43	C	099	63	c
004	04	EOT	036	24	$	068	44	D	100	64	d
005	05	ENQ	037	25	%	069	45	E	101	65	e
006	06	ACK	038	26	&	070	46	F	102	66	f
007	07	BEL	039	27	‘	071	47	G	103	67	^g
008	08	BS	040	28	^(	072	48	H	104	68	h
009	09	HT	041	29	^)	073	49	I	105	69	i
010	0A	LF	042	2A	*	074	4A	J	106	6A	^j
011	0B	VT	043	2B	+	075	4B	K	107	6B	k
012	0C	FF	044	2C	^,	076	4C	L	108	6C	l
013	0D	CR	045	2D	-	077	4D	M	109	6D	m
014	0E	SO	046	2E	.	078	4E	N	110	6E	n
015	0F	SI	047	2F	/	079	4F	O	111	6F	o
016	10	DLE	048	30	0	080	50	P	112	70	p
017	11	DC1	049	31	1	081	51	Q	113	71	q
018	12	DC2	050	32	2	082	52	R	114	72	r
019	13	DC3	051	33	3	083	53	S	115	73	s
020	14	DC4	052	34	4	084	54	T	116	74	t
021	15	NAK	053	35	5	085	55	U	117	75	u
022	16	SYN	054	36	6	086	56	V	118	76	v
023	17	ETB	055	37	7	087	57	W	119	77	w
024	18	CAN	056	38	8	088	58	X	120	78	x
025	19	EM	057	39	9	089	59	Y	121	79	^y
026	1A	SUB	058	3A	^:	090	5A	Z	122	7A	z
027	1B	ESC	059	3B	^;	091	5B	^[	123	7B	^{
028	1C	FS	060	3C	<	092	5C	\	124	7C	^|
029	1D	GS	061	3D	=	093	5D	^]	125	7D	^}
030	1E	RS	062	3E	>	094	5E	^^	126	7E	~
031	1F	US	063	3F	?	095	5F	^_	127	7F	Ñ/DEL

През 1981 г. компания IBM разработва допълнение към 128 символния ASCII код, като удължава кодовата комбинация от 7 до 8-битова. Така се появява втората страница на вече 256 символната ASCII таблица. Втората половина на таблицата включва двоичните комбинации – 1xxx xxxx (80FF). Компания IBM реализира хардуерна поддръжка на 8-битовия символен код в персоналния компютърен модел 5150, получил известност под наименованието IBM-PC, приеман за първия масово произвеждан персонален компютър. Операционната система на този компютър, MS-DOS, използва 8-битовия ASCII код. Най-отличителното във втората страница на кодовата таблица е възможността за включване на азбуки на регионални писмени езици, отлични от английския. Така за нашата страна и за редица държави, използващи кирилица, в таблицата е естествено включването на кирилската азбука. Включени са още множество символи, предназначени за изчертаване, някои често използвани гръцки букви, както и допълнителни математически символи. Подредбата на символите в таблицата не е случайна и се нарича “ASCIIbetical order”.

Втора страница на ASCII – таблицата

10-чен код	16-чен код	Символ	10-чен код	16-чен код	Символ	10-чен код	16-чен код	Символ	10-чен код	16-чен код	Символ
128	80	А	160	A0	а	192	C0	└	224	E0	α
129	81	Б	161	A1	б	193	C1	┴	225	E1	β
130	82	В	162	A2	в	194	C2	┬	226	E2	Γ
131	83	Г	163	A3	г	195	C3	├	227	E3	π
132	84	Д	164	A4	д	196	C4	─	228	E4	Σ
133	85	Е	165	A5	е	197	C5	┼	229	E5	σ
134	86	Ж	166	A6	ж	198	C6	╞	230	E6	μ
135	87	З	167	A7	з	199	C7	╟	231	E7	τ
136	88	И	168	A8	и	200	C8	╚	232	E8	ɸ
137	89	Й	169	A9	й	201	C9	╔	233	E9	θ
138	8A	К	170	AA	к	202	CA	╩	234	EA	Ω
139	8B	Л	171	AB	л	203	CB	╦	235	EB	δ
140	8C	М	172	AC	м	204	CC	╠	236	EC	∞
141	8D	Н	173	AD	н	205	CD	═	237	ED	Φ
142	8E	О	174	AE	о	206	CE	╬	238	EE	ε
143	8F	П	175	AF	п	207	CF	┐	239	EF	Ç
144	90	Р	176	B0	р	208	D0	░	240	F0	º
145	91	С	177	B1	с	209	D1	▒	241	F1	±
146	92	Т	178	B2	т	210	D2	▓	242	F2	³
147	93	У	179	B3	у	211	D3	│	243	F3	£
148	94	Ф	180	B4	ф	212	D4	┤	244	F4	ó
149	95	Х	181	B5	х	213	D5	№	245	F5	õ
150	96	Ц	182	B6	ц	214	D6	§	246	F6	¸
151	97	Ч	183	B7	ч	215	D7	╗	247	F7	»
152	98	Ш	184	B8	ш	216	D8	╝	248	F8	°
153	99	Щ	185	B9	щ	217	D9	┘	249	F9	·
154	9A	Ъ	186	BA	ъ	218	DA	┌	250	FA	×
155	9B	Ы	187	BB	ы	219	DB	█	251	FB	Ö
156	9C	Ь	188	BC	ь	220	DC	▄	252	FC	h
157	9D	Э	189	BD	э	221	DD	▌	253	FD	²
158	9E	Ю	190	BE	ю	222	DE	▐	254	FE	-
159	9F	Я	191	BF	я	223	DF	▀	255	FF	blank

Първите 32 символа на ASCII кода се използват и интерпретират различно. Това е свързано с логиката на работа на конкретния тип периферно устройство. Така например в печатащите устройства има смисъл да се управлява преходът към нова страница (символ FF – From feed, с код 0C). В други устройства понятието страница може да не съществува, например в устройство за работа с магнитна лента. В подобни случаи същият този символ може да се интерпретира по друг начин. В съвременните компютри на тези кодове, освен логическия смисъл, е присвоен и някакъв графичен йероглиф (графема), чрез който те могат да се визуализират в дадена позиция на дисплея или на печатащото устройство. Така например символът SOH (Start of header – начало на заглавна част при комуникации), имащ шестнадесетичен код 01, на екрана на монитора може да бъде изобразен като "усмихнато лице" – ☺.

Смисълът и визията на управляващите символи са представени в следващата таблица.

Визия на управляващите символи от ASCII – таблицата

10-чен код	16-чен код	Символ	Визия	English	Български
000	00	NUL		Null character or time fill	Празен символ; при визуализиране на последователност от символи, позицията, в която той се среща, се игнорира.
001	01	SOH	^☺	Start of header	Начало на заглавна част при комуникации.
002	02	STX	^☻	Start of text	Начало на текста при комуникации.
003	03	ETX	♥	End of text	Край на текста при комуникации.
004	04	EOT	♦	End of transmission	Край на предаването при комуникации.
005	05	ENQ	♣	Enquire	Заявка за комуникация.
006	06	ACK	♠	Acknowledge transmission	Потвърждение на приета заявка при комуникации.
007	07	BEL	^●	Bell	Включва звуков сигнал.
008	08	BS	^◘	Backspace	Връщане с една позиция назад.
009	09	HT	¡	Horizontal tab	Хоризонтален табулатор.
010	0A	LF	^◙	Line feed	Преход на следващия ред.
011	0B	VT	♂	Vertical tab	Вертикален табулатор.
012	0C	FF	♀	From feed	Преход към следваща страница.
013	0D	CR	♪	Carriage return	Връщане на каретката или преход в началото на реда.
014	0E	SO	♫	Shift out	Преход към червена лента или към двойна ширина.
015	0F	SI	☼	Shift in	Преход към черна лента или към сгъстен печат.
016	10	DLE	►	Data line escape	Начало на специален код.
017	11	DC1	◄	Device control #1, ON-Line	Първи сигнал за управление на принтер (активира принтера).
018	12	DC2	↨	Device control #2, Tape	Втори сигнал за управление на принтер (отменя сгъстяването).
019	13	DC3	‼	Device control #3, OFF-Line	Трети сигнал за управление на принтер (дезактивира принтера).
020	14	DC4	¶	Device control #4, Tape	Четвърти сигнал за управление на принтер (отменя двойната ширина).
021	15	NAK	^§	Negative acknowledge	Сигнал за неприета заявка за комуникации
022	16	SYN	–	Synchronization	Синхронизация.
023	17	ETB	,	End of transmission blok	Край на предавания блок.
024	18	CAN		Cancel	О тмяна на предходен символ или група, изчистване на буфер.
025	19	EM	¯	End of medium	Край на носителя.
026	1A	SUB	®	Substiute	Замяна на символ или низ.
027	1B	ESC	¬	Escape	Начало на управляваща последователност
028	1C	FS	∟	File separator	Разделител между файлове.
029	1D	GS		Group separator	Разделител между групи.
030	1E	RS	▲	Record separator	Разделител между записи.
031	1F	US	▼	Unit separator	Разделител между елементи.
127	7F	DEL	∆	Delete	Изчистване.

Използвайки дефинираните кодове, може да се представи всяка символна последователност, имаща смисъл за човека. Обикновено последователностите от символи се наричат символни низове или просто низове. Така например кодовата последователност или символният низ:

87 A4 B0 A0 A2 А5 A9 20 21

означава съобщението: З д р а в е й ! ( Здравей ! )

Читателят неизбежно ще се сблъска с означения, които непосредствено представят кодовите комбинации. На практика те са двоични комбинации и при записване и при четене тяхната дължина съдава определено неудобство. Ето защо, най-често кодовите последователности се изразяват с помощта на 16-чни символи, което позволява четирикратното им скъсяване. За пояснение на това, 16-ната кодова последователност обикновено при записване е следвана от латинската буква h. Например кодовата комбинация

00111001101011100101000111010110

ще се представи от последователността

3 9 A E 5 1 D 6 ,

която ще се записва така: 39AE51D6h.

UNICODE

Положението с масовото навлизане на компютрите и компютърните технологии и в най-отдалечените земни територии не остава без последствия. Използването на компютърни системи в съвремието е неизбежно и животът ни без тях вече е невъзможен. Осембитовите символни кодове се оказват вече крайно ограничени. По данни на ООН на Земята съществуват около 6800 различни езици, а количеството символи, които се използват е около 200,000. Положението се затруднява допълнително от други обстоятелства. Например, съществуват езици, в които различните писмени знаци (графеми) са толкова много и така сложно свързани със смисъла на самия текст, че никаква подмяна на 256-символния набор, за който се говореше в предходния раздел, не би могла да реши проблема с необходимостта от използване на персонален компютър. Необходимо е да добавим още, че науката се нуждае и от възможността да изследва и да използва и “мъртви” (забравени) езици. Казаното токущо ни води до извода, че дължината на кодовата комбинация, с която ще се представят символите от така увеличеното по обем множество, следва да се увеличи. Разработки в това направление се водят отдавна и все още продължават. Обобщаващото наименование на новите стандарти за символно кодиране е UNICODE.

Наименованието Unicode се споменава за първи път през 1988 година като наименование на проект за създаване на универсален набор от символи. Проектът е предложен от компания “Ксерокс”, и представлява предложение за международна многоезикова система за кодиране на текстови символи. Многоезиковата система BMP (Basic Multilanguage Plane) се основавала на 16-битова двоична комбинация, която се определяла като указател на код, или още като широкообхватен ASCII-код. Броят на комбинациите при тази дължина на кода е 2**16=65536, едно число, което не е особено голямо. За развитие на BPM, или за по-ясно, Unicode (Юникод), е създаден консорциум, който публикува в началото на 1991 година стандартът Unicode 1.0, а през следващата година Unicode 2.0. Версиите на Юникод са много и разнообразни (ограничени и разширени). През 2015 г. е публикувана версия Unicode 8.0, а вече е налична и 10-та. Ограничението в кодовата дължина отпада в издание на стандарта от 1996 г. Удължаването на кодовата комбинация обаче води до много сериозни проблеми свържани на първо място с хардуера, а от там и със софтуера. Ето защо за ограничаване на този проблем е реализиран и механизъм за заместващи символи UTF (Universal Coded Character Set + Transformation Format). Така кодирането вече става с променлива дължина. Дължината (форматът) на кодовата комбинация се формира от една или няколко 8-битови кодови единици. Така имаме кодовите системи UTF-8, UTF-16, UTF-32 и UTF-EBCDIC.

До 2007 г. най-използваният стандарт за символно кодиране в световната мрежа WWW (World Wide Web) е бил ASCII (American Standart Code for Information Interchange). Към настоящия момент това е UTF-8. Определя се като система за 8-битово кодиране с променящи се битове (variable-width encoding) и има максимална съвместимост с ASCII.

UTF-16 се определя като 16-битово кодиране с променящи се битове (variable-width encoding).

UTF-32 се определя като 32-битово кодиране с фиксирани се битове (fixed-width encoding).

UTF-EBCDIC се определя като 8-битово кодиране с променящи се битове (variable-width encoding) подобно на UTF-8, но предназначено за съвместимост с EBCDIC (Extended Binary Coded Decimal Interchange Code) - не е част от Юникод.

Юникод дефинира в кодовото пространство (от комбинация 000000 до комбинация 10FFFF) 1,114,112 на брой кодови точки. Символите в стандарта UTF-8 се получават от Юникод по следната схема:

· От комбинация 00000000 до комбинация 0000007F:

0xxxxxxx - 1[B];

· От комбинация 00000080 до комбинация 000007FF:

110xxxxx 10xxxxxx - 2[B];

· От комбинация 00000800 до комбинация 0000FFFF:

1110xxxx 10xxxxxx 10xxxxxx - 3[B];

· От комбинация 00010000 до комбинация 001FFFFF:

11110xxx 10xxxxxx 10xxxxxx 10xxxxxx - 4[B].

Кодова точка е двоична комбинация, от която нататък в кодовата таблица следват комбинации, предназначени за определено множество символи. Кодовите точки се означават така “U+”. Например, ако кодовата точка е нула, т.е. началото на кодовата таблица, то сумата U+0058h ще изразява главна латинска буква Х (вижте първа страница на ASCII-таблицата по-горе). От този брой следва да бъдат извадени 2048 заместващи кодови точки, така че остават 1,114,064. Преди визуализация кодовата комбинация на всеки символ се преобразува с помощта на заместващия механизъм UTF като се превръща в 1, 2, 3 или 4 байтова комбинация на целевата кодировка, която няма да изясняваме тук. Така са кодирани:

· Латинските букви, цифрите и препинателните знаци имащи еднобайтова кодова комбинация;

· Повечето диакритични латински букви, както и буквите на кирилица, гръцките букви, арменските, еврейските, арабските и буквите на някои други азбуки и някои знаци, имащи двубайтова кодова комбинация;

· Други азбуки като африкански, азиатски, американски и някои специални знаци се кодират с три- или четирибайтови кодови комбинации.

При обработка на текст Юникод предоставя уникален код на символ, а не глиф за този символ. Визуализацията на глифа (размер, шрифт и форма) се управлява от специален софтуер, като например уеб браузър или текстов редактор.

Подредбата, кодировката, предназначението, групите, смисъла и прочие въпроси отнасящи се до символите, читателят може да изучи по следните адреси:

The Unicode Consortium: http://www.unicode.org/ ,

Unicode 10.0 Character Code Charts: http://unicode.org/charts .

В много сайтове може да бъде намерена в табличен вид пълната информация заедно с визията на графемите. Началото на подобна таблица е представено по-долу. Поради огромния й обем, е илюстрирана само този малък отрязък.

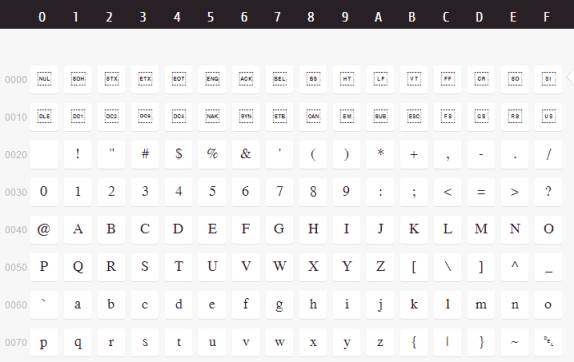
В други таблици, подобни на показаната по-долу, може да бъде видяно разпределението на отделните области в кодовото пространство.

0000 - 001F (0 - 31)	Control character
0020 - 007F (32 - 127)	Basic Latin
0080 - 00FF (128 - 255)	Latin-1 Supplement
0100 - 017F (256 - 383)	Latin Extended-A
0180 - 024F (384 - 591)	Latin Extended-B
0250 - 02AF (592 - 687)	IPA Extensions
02B0 - 02FF (688 - 767)	Spacing Modifier Letters
0300 - 036F (768 - 879)	Combining Diacritical Marks
0370 - 03FF (878 - 1023)	Greek and Coptic
0400 - 04FF (1024 - 1279)	Cyrillic
0500 - 052F (1280 - 1327)	Cyrillic Supplement
0530 - 058F (1328 - 1423)	Armenian
0590 - 05FF (1424 - 1535)	Hebrew
0600 - 06FF (1536 - 1791)	Arabic

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Тъй като няма клавиатура, която да позволява директното въвеждане на всеки Юникод-символ, то операционните системи, както и съответните приложни програми изискват поддържането на алтернативни методи за въвеждане (в текст) на произволни Юникод-символи. Що се отнася до масово разпространената операционна система Microsoft Windows, съдържащата се в нея служебна програма charmap.exe (таблица на символите), поддържа символите на Юникод, но само тези, които са в базовото символно множество (кодове от U+0000 до U+FFFF, т.е. с номера от 0 до 65535 включително). Някои текстови редактори могат да въвеждат в текста символи с клавишната комбинация Alt+X, където Х е 16-чният код на желания символ. В други редактори пък се изисква Х да се набира като 10-чен номер. Например, с комбинацията Alt+064 ще въведете в текущата знакова позиция симвла @. Че това е той, може да видите по-горе в първата страница на ASCII таблицата.

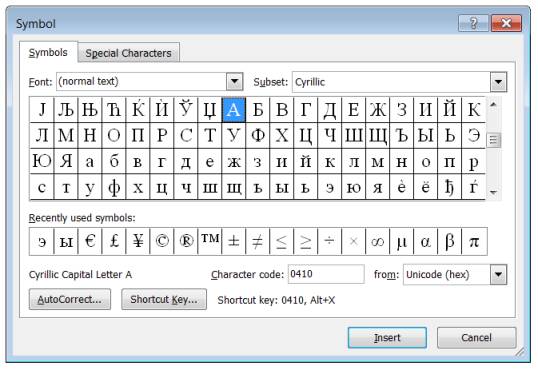
Що се отнася до втората страница на ASCII таблицата, съответствието на символите зависи от актуално активираната езикова клавиатура за текущо използвания текстов редактор. Например, при английска клавиатура (EN) с комбинацията Alt+153 ще бъде въведен и визуализиран символът Щ. За улеснено въвеждане на разнообразни символи в средата на редакторите за потребителите се предлага меню “Insert”. Следващата картинка изобразява формата на менюто, което може да се използва в MS_Word. В долната част се вижда информация за алтернативното въвеждане, за което се говореше малко по-горе. Нормалното въвеждане на избрания символ обикновено става с помощта на бутона Insert на формата.

Както вероятно читателят вече разбира, темата, която тук се опитваме да представим, е много широка и нейното изчерпване няма да бъде възможно за нас, а и не това е нашата цел.

Опериране

След като изложихме въпроса с представянето на символните данни следва да поясним на какви видове обработка се подлагат. Както за логическите данни, така и за символните данни има определено множество от операции. Типичните операции, които могат да бъдат дефинирани за изпълнение върху символни данни са:

- конкатенация – двуместна операция при която от долепването на два символни низа се получава един. Така дължината на символния низ – резултат е равна на сумата от дължините на изходните два низа;

- сравнение – двуместна операция, при която се установява дали два символни низа имат еднакви символи. Обикновено това сравнение се постига чрез символно изваждане. Възможен е вариант, в който се пита, дали два символни низа имат еднаква дължина;

- вмъкване – двуместна операция, при която даден символен низ се вмъква след определена (зададена) позиция в последователността от символи на друг символен низ;

- изхвърляне – изхвърляне на символ от определена позиция (възможни са операции с различни варианти на изхвърлянето);

- прекодиране – подмяна на кодовите комбинации с помощта на определена зависимост. Например текст написан с главни букви може да се замени със същия текст, но написан с малки букви. Това се постига като към всяка кодова комбинация се прибави константата 20h.

Възможни за реализация са и други подобни операции, които се определят от предназначението на дадения процесор.

Искаме да предупредим читателя, че тук от една страна става дума за операции, типични за символни данни въобще, но от друга страна ние всъщност обръщаме внимание на операции върху символни данни, които определяме като технически реализирани. С други думи тук не се имат предвид възможните за изпълнение в един или друг програмен език операции върху символни низове въобще.

Една от основните характеристики на символните низове е тяхната дължина. Дължината се определя в брой символи. Обикновено в общия случай дължината е неограничена, но това съществено затруднява реализацията на споменатите операции. По тази причина реализираните в цифровите процесори действия се делят на две групи – за работа с битове и за работа с полета, като под поле обикновено се разбира разрядната мрежа (регистър) или части от нея. Така се определят действия като:

- извличане, установяване, нулиране или инвертиране на бит по зададен негов номер. Това е операция, при която стойността на поредния бит от съдържанието на двоично поле (регистър) се копира в бит от регистъра на признаците, или му се присвоява стойност 0, 1 или

.

Номерът на бита k се задава като втори операнд, като обикновено се има предвид възходяща номерация в посока отдясно наляво ( … … 4 3 2 1 0);

- намиране на номера на позицията, съдържаща първата срещната единица. При тази операция се извършва последователно претърсване с нарочно преброяване на разрядите на двоичното поле (регистър), започвайки от младшите или от старшите разряди напред, до срещане на разряд, съдържащ единица. Когато полето има например дължина от 32 бита, резултатът е число от 0 до 31.

На базата на тези операции могат да се дефинират производни операции със следните имена например:

- сравнение;

- присвояване на знак и др.

В резултат на операциите върху символни низове се получават нови символни низове или стойности, които потребителят желае да интерпретира по свой собствен начин, определен в съответния алгоритъм. Същото се отнася и до формираните признаци на резултата, за които по-късно в тази книга отново ще се говори.

Следващият раздел е:

1.1.6 Представяне на числовите данни (Presentation of numbers)