1.1.6.1 Числа с
фиксирана
запетая
Presentation
of numbers with fixing point
За представяне на данните се използва двузначна система от символи. Тази система беше обоснована в пункт 1.1.3. Когато с тази система се представят числа, то следва да се разбира, че те се представят в двоична бройна система. В този случай най-общо можем да говорим за двоични числа.
Ще
припомним естествения
вид на
числото

В
този запис с
буква а е
означена коя
да е цифра от
азбуката на q-ичната
бройна
система,
стояща в
позиция с
номер i :
![]()
Следва
да
декларираме,
че няма
теоретични ограничения
за дължината
на записа на
числото и в
двете посоки,
т.е. възможно
е
n ®
¥ и m ® -¥. На
практика
обаче
записът на
дадено число изпитва
ограниченията
на реалния
носител (лист
хартия,
текстово
поле,
регистър и
пр.), което
означава, че
практическите
записи са винаги
с крайна
дължина. От
това веднага
следва
изводът, че
не всяко
число
(разбирайте
количество)
може да бъде
представено
практически.
Така
отнапред е
ясно, че
числата се
разделят на
две групи - представими
и на непредставими.
От
(1.1.6.1.1) се
вижда, че
знакът на
числото е
записан най-отляво,
а разрядите
(позициите)
на числото са
номерирани
както следва:
·
от
запетаята
наляво (за
цялата част
на числото)
във възходящ
ред с цели положителни
числа,
започвайки
от начална стойност
0;
·
и от
запетаята
надясно (за
дробната
част на числото)
в низходящ
ред с цели
отрицателни числа,
започвайки
от начална
стойност –1.
Така
цялата част
на числото е
записана с n
цифри, а
дробната с m.
За това казваме
че числото е (n+m)
разрядно.
Казваме че
позицията с
номер 0 е позиция
на единиците,
тъй като
нейното
тегло според
(1.1.5) е q0=1 за всяко q. Цифрите
(позициите) в
десния край
на записа
определяме
като младши,
а тези в
левия край –
като старши.
Когато
основата q
на бройната
система е 2, разрядите
(позициите)
на записа на
числото се
наричат двоични.
В други
случаи
разрядите
могат да
бъдат десетични,
шестнадесетични,
осмични и пр.
Мястото
(полето),
предназначено
за записване
(представяне)
на числата,
може да се
определи
(опише) като
шаблон (рамка,
дисплей).
Това поле има
дискретна
структура,
чиито
елементи са
отделните
разряди, ето
защо полето
се нарича разрядна
мрежа (РМ).
Основната
характеристика
на разрядната
мрежа (фигура
1.1.6.1.1) е нейната
дължина, която
се измерва с
броя на
разрядите.

Фиг. 1.1.6.1.1.
Представа
за разрядна
мрежа
Онази
част от
разрядната
мрежа, в
която може да
се помести
една цифра на
числото, се
определя
като един
разряд. В
случаи,
когато
числото е
двоично,
разрядът
побира една
двоична
цифра и
неговият размер
се определя
на 1 [bit]. Така
дължината на
разрядната
мрежа може да
бъде
определена в
битове – L=n[b]. Тъй
като
съдържанието
на разрядната
мрежа се интерпретира
според
основата на
бройната система,
следва да се
различават
такива изказвания
като: "n
разряда" и "n бита".
Определяйки
дължината на
разрядната
мрежа в общия
случай на n разряда,
може да се
твърди, че
броят на представимите
в нея числа, е
равен на броя
на
възможните в
нея цифрови
комбинации,
които се
определят
чрез
уравнение (1.1.3.3).
Имайки
предвид
естествения
вид на числото
(1.1.6.1.1),
възниква
въпросът как
да положим
върху него
шаблона на
разрядната
мрежа?
По
принцип са
възможни
следните три
положения:

Фиг. 1.1.6.1.2.
Възможни
положения на
шаблона на РМ
Първото
положение
(вижте горния
правоъгълник)
е такова, че
то в
най-висока
степен
съответства на
естествения
вид на
числото,
защото в разрядната
мрежа ще се
представят
числа, имащи
както цяла,
така и дробна
част.
Второто
положение
(вижте
средния
правоъгълник)
се характеризира
с това, че при
него в
разрядната
мрежа ще се
представят
само цели
числа. Възможностите
му в
сравнение с
първото положение
са много по-големи,
но затова пък
представяните
числа няма да
имат дробна
част, т.е. ще
бъдат по-неточно
представяни.
Третото
положение
(вижте долния
правоъгълник)
е такова, че
разрядната
мрежа е
разположена
само върху
дробната
част, което
означава, че
в нея ще се представят
числата
по-малки от
единица, при това
много
по-точно.
В
крайна
сметка
практическо
приложение намират
последните
две
положения,
при които
запетаята се
намира вън от
разрядната
мрежа.
Имитацията
на
естествения
вид на числото
в разрядната
мрежа, т.е.
съчетаването
и на двете
части на
числото, се
оказва на
практика
неудобно, тъй
като те са
свързани в
повечето
случаи с
различни алгоритми
при
опериране с
тях. Пример
за това са
алгоритмите
от пункт
1.1.2.
И
така,
разрядната
мрежа в
изчислителните
устройства
най-често е
така
организирана,
че положението
на запетаята
на числата
спрямо нея е фиксирано
и неизменно
– отдясно или
отляво. В
този смисъл
говорим за
разрядни
мрежи с дясно
фиксирана
запетая (ДФЗ)
и за разрядни
мрежи с ляво
фиксирана
запетая (ЛФЗ). Структурата
на двата вида
организация
е илюстрирана
на фигура 1.1.6.1.3.
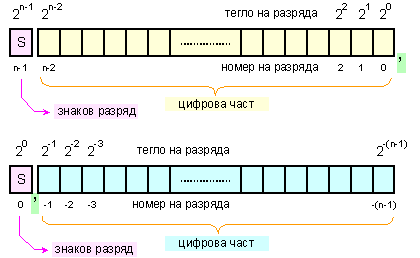
Фиг. 1.1.6.1.3.
Структура
на двоична
разрядна мрежа
Номерацията
на разрядите,
техните
тегла, положението
на запетаята,
съдържанието
на знаковия
разряд – всичко
това е една
условна
интерпретация
на
съдържанието
на
разрядната
мрежа, т.е. на
онова поле,
представено
на фигура 1.1.6.1.1.
За число
представено
в разрядна
мрежа с
показаната
по-горе
структура
говорим, че е
във форма
с фиксирана
запетая.
Освен
със знак,
числата във
форма с
фиксирана
запетая
могат да се
интерпретират
и без знак,
при което
цифровата
част на
разрядната
мрежа нараства
с още един
разряд. Така
увеличаването
на броя на
цифрите, с
които може да
се изобрази
едно число,
увеличава
двойно възможностите
на РМ.
Според
организацията
си всяка
конкретна разрядна
мрежа
притежава
определени
числови
възможности
(характеристики).
На първо
място това са
най-голямото
и най-малкото
числа,
възможни за
представяне
в нея. Интерпретирани
върху
числовата ос:
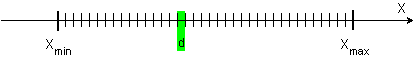
тези две
числа
определят
един
затворен интервал
от нея, който
се нарича диапазон на
представимите
числа:
![]()
За
двоични
числата без
знак,
представяни
в разрядната
мрежа с
дължина L=n[b], диапазонът
се ограничава
от числата (000...0) и
(111...1), т.е.
той е
![]()
Този
диапазон е в
областта на
целите числа,
тъй като,
когато те са
без знак,
най-често се интерпретират
като
представени
с дясно фиксирана
запетая.
Можем да
дадем
конкретен
пример за да
добием
чувство за
възможностите,
например за
една 32 битова
разрядна
мрежа. Тогава
![]()
В
общия случай
възможностите
на дадена разрядна
мрежа с
дължина n q-ични
разряда са
ограничени
от числата
![]()
![]()
които
определят
диапазона на
представимите
числа за нея.
Тук с буква r е
означена
цифрата на
най-голямото
елементарно
количество в
съответната
бройна система
– например 1 за
двоичната, 9 за
десетичната
или F
за
шестнадесетичната.
В случая,
когато
интерпретираме
числата със
знак,
диапазонът
на
представимите
числа се премества
наляво по
числовата ос
така, че се разполага
симетрично
относно
числото нула.
Тъй като за
представяне
на знака на
числото в
разрядната
мрежа се
отделя един
бит (знаците
са два + и -, и се
кодират с
двоичните цифри),
то за модула
на числото ½·½
остават (n-1)
бита. Така
диапазонът
на представимите
в естествен
вид числа се
променя:
![]()
В
случая
числото
![]()
представлява
модула на
най-голямото
двоично
число,
възможно за
цифровата
част на
разрядната
мрежа с дясно
фиксирана
запетая (виж
фигура 1.1.6.1.3).
Така
![]()
В
общия случай за q–ична
бройна
система тези
формули ще
имат следния
вид:
![]()
Когато организацията на разрядната мрежа е с ляво фиксирана запетая, диапазонът на представимите със знак числа е отново симетрично разположен относно нулата, но дължината му е значително по-малка, тъй като в този случай става дума за числа по-малки от единица, т.е.
![]()
В
общия случай
диапазонът
на
представимите
q-ични
числа се
ограничава
от числата
![]()
Представянето
на числа в
разрядна
мрежа с фиксирана
запетая се
характеризира
с равномерна
стъпка
d - дискрет. Дискретът е константа
– най-малкото
по модул
представимо
число, различно
от нула. За
двоичните
числа с дясно
фиксирана
запетая
дискретът d е равен на
единица
![]()
а за числата
с ляво
фиксирана
запетая това е
![]()
т.е. дискретът
и в двата
случая по
същество е
теглото на
най-младшия
разряд в
разрядната
мрежа. В
общия случай
дискретът
съответно е
числото:
![]()
Дискретът
показва още
на какво
минимално разстояние
върху
числовата ос
отстоят две
представими
числа. В този
смисъл те се
наричат съседни,
например 125 и 126.
От казаното
следва, че
представимите
числа са
разпределени
равномерно
в диапазона
от Xmin до Xmax със
стъпка равна
на дискрета. Вътре в този
диапазон има
безкрайно
много други
числа, които
не могат да
бъдат
представени
с
определения
брой разряди.
Те се наричат
непредставими,
а в случай на
нужда могат
да бъдат
заместени от
най-близкото
до тях
представимо
число.
Например
числото -5,785
може да се
замести с числото
6, ако
изискванията
за точност позволяват
(налагат)
това.
Всички
числа, които
са
разположени
върху числовата
ос вън от
диапазона на
представимите
числа – вляво
от него или
вдясно от
него, са също
непредставими
числа. Те обаче не
могат да
бъдат
заместени от
никое
представимо
число, тъй като
изискванията
за точност не
позволяват това.
За тези числа
обикновено
се казва, че препълват
отляво или
отдясно
разрядната мрежа
както е
показано на
фигура 1.1.6.1.4.
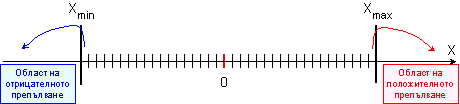
Фиг. 1.1.6.1.4.
Диапазон на
представимите
числа
Тъй
като
получаването
на
непредставими
числа като
резултат от
оперирането
е възможно,
то е задължително
всеки
резултат да
се характеризира
с признак,
който да го
определя като
представим,
т.е. като
верен или
като непредставим,
т.е. неверен.
Традиционно
този признак
се нарича
препълване и
се отбелязва
с буква V, overflow (oVerflow),
който се
кодира както
следва
![]()
Последната
характеристика
на разрядната
мрежа с
фиксирана
запетая се
отнася до точността
за
представяне
на числата.
От казаното
до момента
може да се
съобрази, че
в най-общ смисъл
разрядната
мрежа, поради
своята крайност,
отрязва
младшите
значещи
цифри на числото,
попадащи
вдясно от нея
(виж фигура 1.1.6.1.2). Очевидна
е
безсмислеността
на случая на
отрязване на
старши
значещи
цифри.
Отхвърлената
част от
числото
представлява
всъщност абсолютната
грешка, с
която се
плаща, за да
стане едно
число представимо.
Очевидно е,
че
абсолютната
грешка клони
към теглото
на
най-младшата
позиция
![]()
с което тя
става много
близка до
стойността
на дискрета.
Естествено
има числа,
които се
представят
без грешка,
т.е. точно, ето
защо може да
се обобщи, че
абсолютната
грешка на
двоични (q-ични)
разрядни
мрежи с
фиксирана
запетая се
изменя в
диапазона
![]()
Въпреки
че десните
граници на
дефиниционните
интервали не
са затворени
отгоре,
обикновено
се говори, че
числата с
фиксирана
запетая се
представят с
точност,
равна на
теглото на
най-младшия
разряд в
разрядната
мрежа.
Специално
искаме да
отбележим, че
понятието
абсолютна
грешка, както
и дадените за
нея по-горе
оценки, са
определени в
смисъла на
загубената
при отрязване
част от
числото
(вижте фигура
1.1.6.1.2), т.е. не се
има предвид
възможността
за неговото
представяне
чрез
закръгляне.
Понятието закръгляне
ще бъде
определено
по-късно чрез
математическата
функция round(X,v).
С цел да повишат универсалността на своите процесори, повечето производители поддържат няколко вътрешносхемни формати на числовите данни. Най-често стандартите определят за числата с фиксирана запетая следните формати:
Байт - 8[b]; Byte
Integer (BI);
Дума -
16[b];
Word Integer (WI);
Двойна дума - 32[b]; Double Word Integer (DI);
Дълга дума - 64[b]; Long Integer (LI);
Трябва
обаче да е
ясно, че
различните
формати се
формират
като части
от
разрядната
мрежа.
Поддържането
на формат,
чиято
дължина е по-голяма
от тази на
практически
(апаратно) реализираната
разрядна
мрежа, е
некоректно, тъй
като такъв
формат може
да се
поддържа само
с програмни
средства,
реализиращи
паралелно-последователен
метод на
обработка.
Следващият
раздел е:
1.1.6.2 Числа с
плаваща
запетая
( Presentation of numbers with foating point )