1.1.6.2 Числа с
плаваща
запетая
Presentation
of numbers with floating point
Kогато
съвкупността
от значещи
цифри на числото
се намира
далеко от
разделителя (,),
естественият
вид (1.1.6.1.1)
за неговото
записване е
твърде
неудобен поради
това, че се налага
записването
на голям брой
незначещи
цифри.
Например :
Х1
= 0,000000000035060
или
Х2 = -120740000000000,
.
Очевидно
е и
неудобството
при
опериране с този
вид на
числата, ето защо в
такива
случаи
използваме мултипликативният
вид
числата. Числото се
представя
като
произведение
от значещата
му част и
нейния мащаб.
Например за
горните
числа:
Х1 = 0,000000000035060 =
3506,0 . 10(-14) ;
Х2 = -120740000000000,0 = -12074,0 . 10+(10) ;
където
последователността
3506 или 12074 е
значеща част,
a числата 10(-14) или 10+(10) – мащабен
коефициент или просто мащаб. В
общия случай
мащабът е
степенна
функция с
основа q –
основата на
бройната
система на
числото. Вижда
се, че при
този вид на
числото,
неговата
значеща част
е записана
по-компактно
и бихме могли
да кажем –
по-удобно.
Вижда се още,
че знакът на
числото се
носи от
значещата му
част и няма
нищо общо със
знака на
степенния
показател на
мащаба.
Вижда
се, че като
мащаб не се
използва
произволно
число, а
число, кратно
на основата
на бройната
система (в
примера q=10).
Този избор за
вида на
мащабния
коефициент
не е случаен – направен
е с цел да не се
променят
цифрите в
значещата
част на
числото!
Единствено
при при този
вид на мащабния
коефициент,
при
преминаване
от естествен
към
мултипликативен
вид на
числото,
цифрите на
значещата му
част се
съхраняват. Ефектът
от функцията
на мащаба
видимо се изразява
само в
преместването
на запетаята
в желаното
положение.
Това
положение не
е единствено,
което
означава, че
мултипликативният
вид на едно
число не е
единствен.
Например:
Х1
= 0,000000000035060 =
3506,0 . 10(-14) = 35,060 . 10(-12) = 0,35060 . 10(-10) = ... и т.н.
Така
естествено
възниква
въпросът -
кой от записите
на едно число
е
най-подходящ?
Представянето
на числата в
мултипликативен
вид се нарича
още представяне
във форма
с плаваща
запетая (ПЗ),
наименование,
което
произтича от
свойствата
на така
определения
мащаб.
Мащабът е степенна
функция,
чийто
степенен
показател има
характер на цяло
число със
знак.
Степенният
показател се
нарича порядък
и показва на
колко
позиции е
изместен
разделителят
(запетаята) в
значещата
част (наричана
мантиса),
спрямо
позицията му
(й) в
естествения
вид на
числото (1.1.6.1.1). Думат мантиса,
която
означава
значещата
част на
числото, произхожда
от езика на
древните
етруси
(изчезнал
народ, живял
някога в райните
на северна
Италия) и
означава част
(фракция).
Знакът
на порядъка
показва
посоката на
числовата ос,
в която
следва да се
премести разделителят
(запетаята),
за да се
възвърне естественият
вид на
числото. Съответно:
в
отрицателна
посока ( ¬ )
на числовата
ос, на 14
позиции за
числото X1
X1 = 3506,0 .
10(-14) = 0,00000000003506 ;
и
в
положителна
посока ( ® )
на числовата
ос, на 10
позиции за
числото X2
X2 = -12074,0 .
10(+10) = -120740000000000,0.
Общият
вид на
числото X,
записано във
форма с
плаваща
запетая, е следният:
![]()
където
с Mx е
означена
значещата
част на
числото, т.е. мантисата,
а с px – порядъкът.
За
представяне
на числата в
изчислителните
устройства
отново се
използва
понятието
разрядна
мрежа (виж
фигура 1.1.6.1.1). За
да се представи
дадено число,
в разрядната
мрежа следва
да намерят
място всички
негови елементи,
които според
(1.1.6.2.1) са
четири:
·
знак на
числото;
·
мантиса
на числото;
·
знак на
порядъка и
·
порядък.
Това означава, че разрядната мрежа следва да бъде структурирана в четири части. Преди да представим нейната структура обаче ще изложим още някои съображения.
Като
се има
предвид
ограниченият
брой разряди
на полето за
представяне
на значещата
част на
числото, т.е. на
мантисата, с
цел да се
постигне
максимална
точност при
представянето
й, е
необходимо така
да бъде
подбран
мащабът, че
старшата
цифра на
мантисата да
попадне в
левия край на
полето. Това
означава, че
се цели в
полето да
влязат
възможно
максимален
брой цифри от
числото, т.е.
неговата
най-съществена
част (имаме
предвид
число в
позиционна
бройна
система).
Начинът за
полагане на
полето на
мантисата
върху левия
(старшия)
край на значещата
част на
числото е
показан на
фигурата
по-долу:

Фиг. 1.1.6.2.1.
Полагане на
изобразяващото
поле спрямо
старшата
цифра
Тъй
като в общия
случай няма
предварителни
гаранции, че
всяка
значеща част
ще може да се
помести в
полето на
мантисата, то
е сигурно, че
мантисата ще
представя (ще
изобразява)
значещата
част на
числото неточно,
тъй като
младшата му
част е
възможно да
остане извън
изобразяващото
поле, както
се вижда на
горната
фигура.
Въпреки, че
все още не
сме изяснили
до край
формата за
представяне
на числата,
ще побързаме
със следния извод:
Представянето
на числата
във форма с
плаваща
запетая е
неточно.
Допусканата
грешка е принципна
и не може да
бъде
отстранена.
Тя може само
да бъде
намалена
чрез
удължаване на
полето на
мантисата.
Получаването
на мантисата
по начина,
представен
на фигура 1.1.6.2.1,
се постига
технически
по-лесно, ако
значещата
част е число
с ляво
фиксирана
запетая.
Въпреки, че
това
твърдение
към момента
не е
обосновано
достатъчно
добре,
читателят следва
да го приеме.
Когато
една мантиса
е
разположена
в изобразяващото
поле по
описания
по-горе
начин, тя се
нарича нормализирана.
Това
определение
има и своето
формално описание
при следните
предпоставки
– ако полето
на мантисата
има дължина m разряда и
ако то е
организирано
с ляво фиксирана
запетая,
тогава
мантисата,
представена в
него, е
нормализирана,
ако
удовлетворява
неравенството:
![]()
Организацията
с ляво
фиксирана
запетая за
полето на
мантисата е
избрана от
чисто практически
съображения –
чрез нея
много по-лесно
се постига
условието (1.1.6.2.2),
следейки старшата
цифра на
значещата
част в
числото.
При
това
положение
порядъкът на
числото X с
нормализирана
мантиса е
резултат от
процеса на
удовлетворяване
на
неравенство
(1.1.6.2.2). Тъй
като
мантисата
представлява
число със
знак, то
най-левият
разряд на
полето, което
я съдържа, е
знаков. От
тук следва,
че най-голямата
нормализирана
мантиса представлява
числото:
![]() .
.
Освен
мантисата, за
представяне
на едно число
с плаваща
запетая е
необходимо
да се представи
и неговият
порядък. Тъй
като порядъкът
е число със
знак, а
неговият
характер го
определя
като цяло
число, то
полето, в което
ще бъде
изобразяван,
следва да
бъде организирано
с дясно
фиксирана
запетая. Ако
се приеме, че
неговата
дължина е k
разряда, то
максималният
порядък,
който може да
бъде
представен, е
![]()
При тези
величини
може да бъде
дефинирано максималното
представимо
число във
форма с
плаваща
запетая,
изобразено в
бройна система
с основа q,
така:
![]()
Обикновено
абстрактното
поле на
разрядната
мрежа на
цифровите
машина е едно
и също, т.е. то съчетава
изобразяване
на числа
както във форма
с фиксирана
запетая, така
и във форма с
плаваща
запетая. От
тук следва,
че нейното структуриране
на подполета
за представяне
на
елементите
на числата с
плаваща запетая
е само
формално.
Тогава
сумата от
дължините m+k=n, а
организацията
на
разрядната
мрежа има вида
![]()
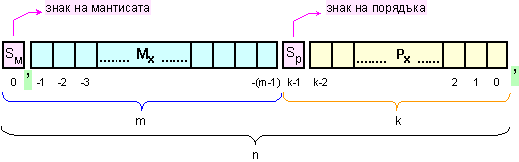
Фиг. 1.1.6.2.2.
Структура
на разрядна
мрежа с плаваща
запетая
При така изяснената структура възможностите на разрядната мрежа се определят от диапазона на представимите в нея числа:
![]()
Подреждането
на четирите
подполета,
представляващи
отделните
елементи на
числото с
плаваща
запетая (± М, ± р), е
конструктивен
проблем.
Освен
показания
начин, може
да бъде
използвано и
следното
подреждане (± [± p], M).
Практическото
използване
на тези
структури ще
бъде
коментирано
отново в
последствие,
след
излагане на
някои
допълнителни
съображения
и теми.
Към
настоящия
момент
естествено
възниква интерес
към въпроса
как се
разделя
общата дължина
на
разрядната
мрежа от n разряда на
две части от
по m и k разряда.
Това
разделяне е
свързано с
определяне
на числовите
характеристики
на разглежданата
организация.
От анализа на
условието за
нормализирана
мантиса (1.1.6.2.2) се вижда, че
изменението
на
количеството
Х – (1.1.6.2.3),
вследствие
изменение на
модула на
мантисата, е
значително
по-слабо,
отколкото
при изменение
на порядъка.
Следователно,
ако искаме да
разширим
диапазона на
представимите
числа, следва
да удължим
полето за
представяне
на порядъка.
Това обаче
може да стане
само за
сметка на
полето на
мантисата. Но
скъсяването
на полето на
мантисата е в
противоречие
с желанието
да
представяме
числата
възможно по-точно,
т.е. с повече
цифри. Тези
две желания
явно са
противоречиви
и тяхното
противоречие
се разрешава
с подходящ
компромис. Арбитър
в
постигането
на този
компромис е относителната
погрешност d,
която трябва
да бъде
приета като
допустима
пределна
граница при
представяне
на числата
във форма с
плаваща
запетая.
Величината d се определя
от
изискванията
за точност на
изчисленията
в дадена
област, в
която ще намери
приложение
изчислителната
машина с изследваната
организация
на
разрядната мрежа.
Така
например, d=10(-3) е
точност,
която може да
удовлетвори
обикновените
счетоводни
изчисления,
но е незадоволителна
в
обикновените
инженерни
изчисления.
Преди
да бъде
оценена
относителната
точност на
числата
представяни
във форма с
плаваща
запетая, е
необходимо
да се пояснят
другите
числови
характеристики
на тази
форма.
Фактът, че
общата
дължина на
разрядната
мрежа при
този вид
организация
остава
същата,
означава, че
общият брой
цифрови комбинации,
които могат
да се
изобразят в
нея, остава
същият, който
беше
определен за
формата с
фиксирана
запетая (виж
уравнение (1.1.3.3)),
т.е. броят на
представимите
числа не се
променя.
Мултипликативният
вид на техния
запис обаче
води до
тяхното неравномерно
разпределение
върху числовата
ос.
Диапазонът
на
представимите
числа се разделя
на толкова
зони,
наричани бинади
за двоичната
бройна
система (или
декади за
десетична
система),
колкото са
различните
стойности на
порядъка.
Следователно
зоните са qk на брой. Във
всяка зона се
представят
един и същи
брой числа.
Този брой се
определя от дължината
на полето на
мантисата, но
при условие (1.1.6.2.2). Така
броят на
числата с
нормализирана
мантиса е 2.q(m-2) – в
това
количество
са включени
положителните
и
отрицателните
числа. С
други думи
това са
всички
цифрови
комбинации в
полето на мантисата,
които
удовлетворяват
условието за
нормалност. Казаното
пояснява още,
че дискретът
на представимите
числа във
форма с
плаваща запетая
не е
постоянна
величина, той
е функция от
стойността
на порядъка.
В рамките на
дадена зона,
дискретът е
константа.
Тъй като дискретът
всъщност е
характеристика
на мантисата,
то той е
пропорционален
на теглото на
младшият й
разряд, т.е. на q-(m-1) (или 2-(m-1) за
двоична
бройна
система).
Като се
отчете и
порядъкът, се
получава
окончателният
вид на
дискрета:
![]()
за
числа,
представени
в произволна
зона р.
Описаното
пояснението
може да се
илюстрира
примерно
така:
![]()
От
рисунката
може да се
разбере, че
разликата в
дължината на
отделните
зони е q пъти. Във
всяка зона с
равномерна
стъпка е представен
един и същи
брой числа, но
като цяло
числата са
разположени
неравномерно.
Следващата
характеристика
на формата с
плаваща
запетая се
отнася до
потребителските
тежнения за
по-голям
диапазон на
представимите
числа. Едва
ли числото 4294967295
(без знак) или
числото ±2147483647
(със знак),
характеризиращи
възможностите
на 32 битовата
разрядна
мрежа с
фиксирана
запетая,
удовлетворяват
изискванията
на потребителя
спрямо
горната
граница на
модула на числата.
Все пак
най-голямото
64-битово число
(18446744073709551615) не малко,
но форматът,
в който то се
представя,
тепърва ще се
практикува
пълноценно.
Ето защо от
формата с плаваща
запетая се
очаква
разширяване
на диапазона
на
представимите
числа. С
други думи
конструирането
на разрядна
мрежа с плаваща
запетая (РМ с
ПЗ) следва да
се извърши в
условията на
следното
неравенство:
![]()
![]()
И
така, търси
се условието,
при което
желаното се
постига. В
първо
приближение,
имайки предвид,
че дължините n и m са
значително
по-големи от 1,
могат да се
извършат
полаганията:
![]()
при
което
горното
неравенство
приема вида:
![]()
Пренебрегвайки
в лявата част
стойността на
множителя q(-1) по
отношение на
множимото,
получаваме
неравенството
![]()
от което може да се синтезира конструктивното изискване към дължината на полето на порядъка, а именно, дължината k следва да се определя така, че да е в сила неравенството:
![]()
Тогава,
ако q=2 и n=32[b],
то десният
израз в
горното
неравенство
получава
стойността
![]()
от
което следва,
че полето на
порядъка
следва да
бъде по-дълго
от 6 [b].
Нека
приемем за
пример
разрядна
мрежа с
типична
дължина от n=32[b]. В
такава
разрядна
мрежа, за
представяне
на числа във
форма с
плаваща
запетая,
обикновено
са отделени 8
бита за
представяне
на
порядъка на
числото т.е. k=8[b].
При тази дължина
на полето за
порядък,
максимално представимият
порядък е
![]()
и горната
граница на
диапазона на
представимите
числа
отскача
почти до
числото
![]()
Ясно
е, че това
число е
несравнимо
по-голямо от
числото
![]()
което беше
пределът на
формата с
фиксирана
запетая при
същите
първоначални
условия –
основа на
бройната
система q=2 и
дължина на
разрядната
мрежа n=32[b].
Ако
числото
(![]() )
)
е
равно на
числото 2147483647, което е
равно на
![]()
то
следва да го
сравним с
числото
![]()
Тъй
като това
число е
двоично, а
двоичните числа
оценяваме
трудно, ще
направим
това между
десетичните
числа, като
решим
уравнението
![]()
спрямо
неизвестния
десетичен
порядък s.
Логаритмуваме
уравнението
при основа 2 и
получаваме
![]()
а
по-нататък:
![]()
откъдето
следва s=127.0,301029996=38,23081.
Замествайки
получената
стойност в
уравнението,
получаваме
търсения
приблизителен
десетичен
еквивалент
![]()
Сега
вече можем да
преценим, че
това е едно
наистина
голямо число
!
Основният
извод, който
можем да направим
е, че ако
формата с
фиксирана
запетая има
предел от 10
десетични
порядъка, то
формата с плаваща
запетая, при
същата
дължина на
разрядната
мрежа n=32[b], повишава
възможностите
си с още цели 28
десетични
порядъка!
Ако
дължината на
полето на
порядъка е
избрана така
както беше
описано
по-горе,
тогава дължината
на полето на
мантисата е
следствие, т.е.
m = n-k =
24[b].
В
светлината
на
представените
по-горе числови
характеристики,
т.е. при
избрано q, при
избрано n, при
избрано k и
получено m, може да
бъде оценена
точността на
представяните
числа. Вече
беше
пояснено
(фигура 1.1.6.2.1), че
абсолютната
грешка е
съизмерима с
дискрета на
формата. От
функцията на
дискрета – (1.1.6.2.5) се
разбира, че
абсолютната
грешка се
изменя в
твърде
широки
граници:
![]()
Абсолютната
грешка е
нула, когато
двоичната
мантиса на
числото се
побира в
(m-1)-битовото
поле (виж
фигура 1.1.6.2.1).
Максималната
абсолютна
грешка е
цялото число
![]()
Ако
се
придържаме
към взетите
за пример по-горе
дължини, за двоична
бройна
система това
е числото
![]()
наистина
впечатляваща
загуба !
Отново
специално
искаме да
отбележим, че
понятието
абсолютна
грешка, както
и дадената за
нея по-горе
оценка, са
определени в
смисъла на
загубената
при отрязване
част от
числото
(вижте фигура
1.1.6.2.1), т.е. не се
има предвид
възможността
за неговото
представяне
чрез
закръгляне.
Понятието закръгляне
ще бъде
определено
по-късно чрез
математическата
функция round(X,v).
Тъй
като обаче
абсолютната
грешка е
функция от порядъка
на числото,
то по-важна е
относителната
й оценка
спрямо
представеното
число. Ето
защо
точността на
представяните
в разрядната
мрежа с
плаваща
запетая
числа се оценява
чрез
относителната
погрешност. Относителната
погрешност
на РМ с ПЗ се
определя като
отношение на
максималната
абсолютна грешка,
с която се
представя
дадено число
и модула на числото.
Ако търсим
максимално
възможната
стойност на
относителната
грешка следва
да
предположим
такова число,
което има минимална
мантиса, но
при това отговаряща
на условието
за
нормалност
(1.1.6.2.2).
Ако
дискретът (1.1.6.2.5)
е оценка за
възможно
най-голямата
загуба от
значещата
част при представянето
на дадено
число X, тогава
изразът за
относителната
погрешност
получава
вида:
![]()
Основният
извод, който
се налага от
получения
израз, е, че
относителната
погрешност,
за разлика от
абсолютната, не
е функция на
порядъка и
зависи
единствено
от дължината
на полето на
мантисата,
т.е. от
конструктивните
параметри на
разрядната
мрежа. Тъй
като има числа,
които се
представят
точно, то в
общия случай
относителната
погрешност
се определя
подобно на
абсолютната
в интервала:
![]()
В
условията на
даденото
по-горе като
пример
структуриране
на 32
битовата
разрядна
мрежа, т.е. при m=24[b], относителната
погрешност
се оценява
със стойността
![]()
Оценката на относителната погрешност може да се получи в десетична бройна система аналогично на абсолютната, чрез формулата
![]()
където с m е
означен
броят на
двоичните
разряди.
Формула
(1.1.6.2.13), както и
формула (1.1.6.2.9)
свързват двоичния
порядък на
едно число с
десетичния порядък
на същото
число. Тази
връзка се
извежда
единствено
заради нас
самите, тъй
като ние сме
свикнали да
възприемаме
оценките в
десетична бройна
система.
Тази връзка
може да се
изрази в
следните нови
формули:
![]()
Когато
порядъкът се
отнася за
число с нормализирана
мантиса, т.е.
мантиса,
удовлетворяваща
условието (1.1.6.2.2),
тогава
неговата
стойност
съответства
на дължината
на полето, в
което се
помества
цялата част на
изобразеното
число.
Например,
ако X=0,110011.2(+8) ,
то цялата
част на
числото във
форма с фиксирана
запетая – X=11001100,00
, съдържа 8
цифри. Това
изказване е в
сила
независимо каква
е бройната
система, ето
защо формула (1.1.6.2.14)
може да се използува за
определяне
на броя на
десетичните
или на
двоичните
разряди на
полето, в което
ще се
изобразява
дадено число
при една и
съща точност
или когато то
се
преобразува
от едната
бройна
система в
другата.
Следователно
формула (1.1.6.2.14)
може да се
запише по
следния
начин
![]()
където с L(2) е означена
дължината на
двоичното
поле в битове,
а с
L(10) – дължината
на
десетичното
поле в 10-чни
разряди. От
вида на тази
формула
следва
твърдението,
че m на брой
двоични
разряда са
еквивалентни
на (0,301029996.m)
десетични
разряда и
обратно – d на
брой
десетични
разряда са
еквивалентни
на (3,3222591.d) двоични.
Като се вземе
предвид, че
току що
записаните
коефициенти
не са цели стойности,
а порядъците
(респективно
дължините)
имат точно
този смисъл,
то следва, че
знакът равно
в (1.1.6.2.14) и (1.1.6.2.15) не
бива да се
абсолютизира.
Представянето
на едно число
във форма с
плаваща
запетая е
свързано
преди всичко
с процеса на нормализиране
на неговата
значеща част
и получаване
на мантиса,
която
удовлетворява
неравенството
(1.1.6.2.2). Този
процес практически
се изразява в
последователно
изместване
на значещата
част на
числото в полето
за мантисата
наляво или
надясно на
един разряд,
така че
най-старшата
значеща цифра
на числото да
застане
вдясно до
запетаята на
полето. Тъй
като всяко
едно изместване
на една
позиция
променя
порядъка на
числото с
една единица,
то за да се
запази на всяка
стъпка
неизменно
означеното
според (1.1.6.2.1)
количество, е
необходимо
да се извършва
и
съответната корекция
на порядъка.
При
изместване
на значещата
част на един
разряд
наляво,
корекцията
на порядъка е
според
израза (px-1)
, а при
изместване
надясно –
според
израза (px+1).
Очевидно
процесът на
нормализация
е свързан с
изпълнение
на операция
събиране и
операция
изваждане в
полето на
порядъка и с
това той е
твърде опасен.
Опасността
се изразява
във възможността
да настъпи препълване
в полето на
порядъка.
Интересно е
да се
интерпретират
поотделно
случаите на
това
препълване.
Така например,
при положително
препълване
в полето на
порядъка,
фактически
числото е толкова
голямо, че то
излиза
отляво или
отдясно на
диапазона на
представимите
с плаваща
запетая
числа, т.е.
![]()
където Xmax е
определено с
(1.1.6.2.3). Тази ситуация
се нарича препълване
при плаваща
запетая.
Признаците,
по които се
разпознава
това препълване,
нямат нищо
общо с
признаците
при работа с
фиксирана
запетая.
Аналогично
на препълването
при
фиксирана
запетая и тук
диапазонът
на
представимите
числа може да
бъде
надхвърлен
отдясно или
отляво, което
ни дава право
да говорим за
положително или
за
отрицателно
препълване
при плаваща
запетая
съответно
(вижте фигура
1.1.6.1.4).
При
отрицателно
препълване
в полето на
порядъка
фактически
става дума за
число, което
според
записа (1.1.6.2.1), има
толкова
голяма по модул
отрицателна
степен, че
може да се
интерпретира
като безкрайно
малко число.
Такова число
практически
е по-близо до
абсолютната
нула,
отколкото до
най-малкото
представимо
(по модул)
число. Това
число се
заменя с едно
число,
наречено машинна
нула. Машинната
нула е число, което
се дефинира
така
![]()
На
пръв поглед,
като че ли
при нулева
мантиса
стойността
на порядъка е
без значение.
Това е вярно
при чисто
математическото
интерпретиране
на
стойността
на израза. За
нейната
техническа
реализация
обаче не е
така.
Мотивите за този
вид на
машинната
нула се
съдържат в алгоритъма
за събиране
на числа,
представени
във форма с
плаваща
запетая,
който ще бъде
пояснен в
глава 3.
Казаното
по-горе означава,
че
при
отрицателно
препълване в
полето на порядъка не
настъпва препълване
при плаваща
запетая!
Вече
стана ясно,
че порядъкът
има характер на
цяло число
със знак. Както
ще бъде
изяснено
по-късно в
тази книга
(вижте глава
3),
използването
на порядъка в
неговия
естествен
вид има
своите
недостатъци.
Ето защо
порядъкът се
представя
неявно чрез
друга
величина,
наречена характеристика,
чиито
стойности са числа
без знак. Превръщането
на порядъка в
число без
знак се
постига чрез
изместване
на неговия
диапазон в
положителната
посока на
числовата ос.
Новополучената
величина се
нарича изместен
порядък или характеристика
и се определя
така:
H
= p+D ,
(1.1.6.2.17)
където с D е
означена
константа,
която се
нарича изместване.
Изместването
D
се дефинира
като
най-малкото
число, с
помощта на
което се
постига
неравенството
H ³ 0, за
всяко
възможно p.
Очевидно е,
че
стойността
на
изместването D
зависи от
конструктивните
параметри на
разрядната
мрежа и
по-точно от
дължината на полето
на порядъка,
откъдето
следва, че
неговата
стойност е
равна на
числото,
представляващо
теглото на
знаковия
разряд в
полето на
порядъка, т.е.
![]()
За примера, разгледан
по-горе, при k=8,
изместването
получава
стойност
![]()
Така
8 битовото
двоично
число без
знак H
се определя в
диапазона [00000000 … 11111111],
който в
десетична
система е [0 … 255].
Премахвайки
знака на
порядъка,
структурните
елементи на
числото,
които следва
да се представят
в разрядната
мрежа,
остават три.
Тяхното
подреждане в
разрядната
мрежа най-често
е по начина,
показан на
фигура 1.1.6.2.3.
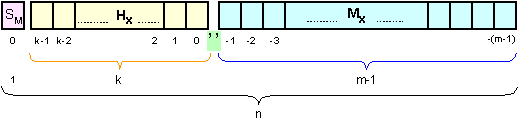
Фиг. 1.1.6.2.3.
Структура
на РМ с ПЗ и
изместен
порядък
Следва
да отбележим,
че
структурирането
на
разрядната
мрежа е
конструктивен
проблем, т.е.
подреждането
на
елементите
на числото в
разрядната
мрежа не
зависи от
формата, в
която то е
изразено, а
от
конструкцията
на
изчислителното
устройство,
опериращо с така
представените
числа.
При
представяне
на числата
във форма с
плаваща
запетая, така
както и при
числата с
фиксирана
запетая,
производителите
на
технически
средства
поддържат в
разрядната
мрежа
различни вътрешно-схемни
формати на
данните.
Освен това в
организацията
и
структурирането
на разрядната
мрежа,
за всяка от
формите,
са въведени
редица
особени
подробности,
свързани най-вече
с желанието
да се повиши
точността на изчисленията.
Някои от тях
ще бъдат
пояснени тук,
а други –
по-късно,
когато
пристъпим към
синтеза на
операционните
устройства. Една
от тези
особености е
изместеният
порядък,
чиято
същност вече
изяснихме.
Особеното в
него е това,
че в
разрядната
мрежа не се представя
порядъкът р,
както следва
от (1.1.6.2.1), а характеристиката
Н.
Втората
особеност,
която ще
изясним сега,
се нарича "скрит
бит" на
мантисата (HB – Hidden
Bit).
Скритият бит
на мантисата
присъства
само по време
на
изчисленията.
При
запомняне на числата
в паметта
скритият бит
не се съхранява.
Основанията
за подобно
манипулиране
на мантисата
на числото се
съдържат в
условието за
лява
нормализация
(1.1.6.2.2). Според
това условие
всяко
представено
число, различно
от нула, има
нормализирана
мантиса, която
може да
представим
така:
![]() . (1.1.6.2.19)
. (1.1.6.2.19)
Гледайки
този вид на
мантисата,
стигаме до извода,
че всяка
мантиса,
различна от
нула, има за
старша цифра
единица – 1 (при
двоична
бойна
система).
Тогава
възниква
въпросът – защо
е необходимо
да се запомня
този бит, след
като за всяко
число той е 1?
Така се стига
до решението
за два
формата на
данните –
формат за
запомняне (Memory Format - MemF), при който
тази старша
единица не
присъства в
паметта
(скрива се) и формат за
опериране с
числата (Operation Format – OpF), при който
тази единица
присъства
(възстановява
се) в
операционното
устройство. Разликата
между двата
формата е в
това, че
първият е с
един бит
по-къс.
Скритият бит,
като
неизменна
старша
единица в
мантисата на
всяко число,
се приема да
се
възстановява
отляво на
запетаята
на мантисата.
Така нейният
подразбиращ
се вид се
променя и
след
казаното се
определя така:
![]() , (1.1.6.2.20)
, (1.1.6.2.20)
В
този си вид
мантисата
присъства
във формат OpF.
Задължителната
единица се
явява в
цялата й
част.
Дробната
част от
стойността
на мантисата
е означена с буква F (Fraction). Това е
онази част,
която
подлежи на
запомняне и
присъства
само във
формат MemF. Този
начин за
манипулиране
на мантисата
на числата
наричаме техника
на скрития
бит.
Тъй
като този вид
на мантисата
се получава от
определението
за
нормалност (1.1.6.2.2) в
резултат на
изложените
по-горе
мотиви, то
следва, че
трябва да
приемаме за
нормализирализирана
всяка
мантиса,
чиято
стойност е записана
в
съответствие
с
определението
(1.1.6.2.20).
Този
вид на
мантисата
обаче не
остава без последствия.
Ако искаме да
продължаваме
да представяме
същото число,
то
преместването
на запетаята
на мантисата
на един бит
надясно
следва да
бъде компенсирано
в стойността
на порядъка
чрез изваждане
на единица.
Трябва да
съзнаваме
добре, че
това
изваждане на
единица от
стойността
на порядъка
ще се прави
за всяко
число, т.е.
тази
операция е
задължителна.
Тъй като обаче
в разрядната
мрежа се
представя
характеристиката,
то нейното
определение
(1.1.6.2.17) ще модифицираме
така, че да
запазим
цялостта на
порядъка:
H
= (p-1)+D = p
+ (D-1)
, (1.1.6.2.21)
Това
определение
на
характеристиката
изменя
нейния
диапазон в
сравнение с
определенията
(1.1.6.2.17) и (1.1.6.2.18).
Диапазонът
се определя
от две
величини –
порядък p и
изместване (D-1). Тъй като
възможностите
на порядъка
не са променени,
а
изместването
е намалено с
единица, то
следва, че
горната и
долната
граници на
диапазона на
характеристиката
са намалени с
единица. За
взетия по-горе
пример, при
дължина на
полето от k=8[b],
възможните
стойности на
характеристиката
са затворени
в интервала
[00000001 … 11111110],
т.е. [1 … 254]. Това
съответства
на порядъци в
диапазона [-126 … +127].
След
всичко
казано
следва, че
едно число във
форма с
плаваща
запетая, с
нормализарана
мантиса, с
изместен
порядък и с
техника на скрития
бит, ще се
определя
така:
![]()
Представянето
на числата
според така
получената
форма се
реализира в
разрядна мрежа
със следната
структура:
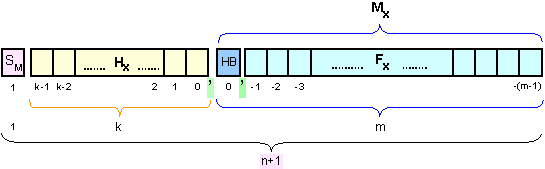
Фиг. 1.1.6.2.4.
Структура
на РМ с ПЗ, с
изместен
порядък и
скрит бит
Структурата
на
разрядната
мрежа от
фигура 1.1.6.2.4
е
стандартизирана
от
американската
организация IEEE (Institution of Electrical and Electronic Engineers). Стандартът
е известен в
литературата
под номер 754 (IEEE 754 и по-новия 854) и се спазва
от всички
производители
на компютърна
техника.
Главното
предназначение
на стандарта
е да осигури
преносимостта
на програмите.
Стандартът
определя два
формата за двоични
числа –
формат ”единична
точност” (SP – Single Precision) с дължина 32[b]
и ”двойна
точност” (DP – Double Precision) с дължина 64[b].
Във формат SP
са
определени 8[b] за
представяне
на
характеристиката,
а във формат DP – 11[b].
Това което
прави
впечатление
е, че форматът
с двойна
точност
предлага
значително разширение
на диапазона
на
представимите
числа. В 11
битовото
поле максималният
порядък,
който може да
се представи
е 1023. Тогава при Mmax »
2 (според
(1.1.6.2.20)) можем да
разчитаме на
![]()
Стандартът
предоставя
допълнителна
свобода на
производителите
като
определя в
допълнение
на основните
формати
още два,
неречени ”разширени”
– SEP (Single Extended Precision) и DEP (Double Extended Precision).
Характерното
за тези
разширени
формати е
това, че
дължините на
полетата не
са фиксирани,
но са ограничени
отдолу.
Параметрите
на форматите
на стандарта
са сведени в
таблица 1.1.6.2.1.
Таблица
1.1.6.2.1
Стандартни
формати
|
|
Single |
Single
Extended |
Double |
Double
Extended |
|
Дължина
на
разрядната
мрежа |
32 |
≥ 43 |
64 |
≥ 79 |
|
Дължина
на полето H |
8 |
≥ 11 |
11 |
≥ 15 |
|
Дължина
на полето F |
23 |
≥ 31 |
52 |
≥ 63 |
|
Стойност
на
изместването
D |
127 |
неопределена |
1023 |
неопределена |
|
Максимален
порядък |
127 |
≥ 1023 |
1023 |
≥ 16383 |
|
Минимален
порядък |
-126 |
≤ -1022 |
-1022 |
≤ -16382 |
|
Основен
диапазон на
числата |
|
неопределена |
|
неопределена |
Както
може да се
разбере от таблицата,
стандартът
определя форматите
от вида MemF, т.е.
фоматите,
които са
непосредствено
свързани с
програмите.
Що се отнася
до техническата
реализация
на
разрядната
мрежа, производителите
имат пълна
свобода.
Появата по време на изчисления на скрития бит в разрядната мрежа на техническото средство води до увеличаване на дължината на мантисата с един разряд, с което реалната точност при изчисленията се увеличава с една единица на двоичния порядък (вижте (1.1.6.2.11)). Ако в паметта например се съхранява число във формат SP, имащ 32-битовото съдържание
1 10000010 10010000000000000000000 ,
то след зареждането му в разрядната мрежа, скритият разряд се възстановява според уговорката и изчисленията се провеждат върху 33-разрядното число:
|
S |
H |
HB |
F |
|
1 |
10000010 |
1 |
10010000000000000000000 |
Според (1.1.6.2.22) този запис
съответства
на числото:
![]()
Интересен
е въпросът –
как се
реализира на
практика
стандарта? В
повечето
реални процесори
за
представяне
на числата
във форма с
плаваща
запетая е
реализирана
разрядна
мрежа с обща
дължина от 80[b], чиято
структура е в
пълно
съответствие
с показаната
на фигура 1.1.6.2.4.
Избраните за
подполетата
дължини са
следните: за
характеристиката
Н тя е k=15[b];
за мантисата (M=1,F) тя е m=64[b].
Така общата
дължина е m+k+1=64+15+1=80. От тези
стойности
става ясно,
че на практика
е реализиран
разширеният
формат с двойна
точност DEP (Double Extended Precision). Що се отнася
до по-късите
формати,
които потребителят
може да
поиска (в
своите
програми) за
стойностите
на отделни
величини, то
с това
тяхното получаване
е осигурено.
Това се
извършва с помоща
на специални
алгоритми за
преобразуване
на форматите,
които ще
разгледаме
по-късно.
Тук
следва да
направим
пояснение на
поредната
особеност.
Когато
съдържанието
на 80 битовата
разрядна
мрежа трябва
да се запамети
като
стойност на
дадена
величина, то
тя заема 10
байта в
паметта.
Вероятно
читателят се
досеща, че в
този си
формат
числото е
съхранено
заедно с бит
НВ. Искаме да
кажем, че
само в този
случай MemF и OpF форматите
на числата
съвпадат. В
този 80 битов формат
и поле на
характеристиката
с дължина 15 [b],
максималният
порядък,
който може да
се представи
е 16383. Тогава при
Mmax » 2 (според (1.1.6.2.20))
максимално
възможното
число, което
определя
диапазона на
представимите
числа е
![]()
Така
изложената техника на
скрития бит
повдига
въпроса за крайните
(граничните)
стойности на
характеристиката:
![]()
Тези
двоични комбинации
в полето Н са
напълно
възможни и не
могат да
бъдат изключени
от
разглеждане.
Тези две
стойности са резервирани
и ситуациите,
при които те
възникват, се
наричат изключителни.
Така
например,
максимално
възможната
стойност на
характеристиката
(255; 2047 и 32767,
съответно за
различните
формати), е
резервирана
за
интерпретация
на две
допълнителни
абстрактни
величини – безкрайност и NAN (Not
a Number) – “не е
число”.
Минимално
възможната
стойност на
характеристиката
Н=0 пък
се използва
за
изобразяване
на числото
нула, при
условие
обаче, че F=0. В тези
случаи стойността
на скрития
бит е без
всякакво значение.
По-подробно
интерпретацията
на съдържанието
на
разрядната
мрежа е
представено
в таблица 1.1.6.2.2.
Таблица 1.1.6.2.2
Параметри
на форматите
|
|
Единична
точност (32 [b]) |
Двойна
точност (64 [b]) |
||||||
|
|
Знак |
Н |
F |
Стойност |
Знак |
Н |
F |
Стойност |
|
+ 0 |
0 |
0 |
0 |
+ 0 |
0 |
0 |
0 |
+ 0 |
|
– 0 |
1 |
0 |
0 |
– 0 |
1 |
0 |
0 |
– 0 |
|
|
0 |
255 |
0 |
|
0 |
2047 |
0 |
|
|
|
1 |
255 |
0 |
|
1 |
2047 |
0 |
|
|
NaN (Quiet
NaN) |
0 or 1 |
255 |
≠ 0 |
NaN |
0 or
1 |
2047 |
≠
0 |
NaN |
|
NaN (Signaling
NaN) |
0 or 1 |
255 |
≠ 0 |
NaN |
0 or
1 |
2047 |
≠ 0 |
NaN |
|
( +X ) ≠ 0, нормализирано |
0 |
[1…254] |
f |
|
0 |
[1…2046] |
f |
|
|
( –X ) ≠ 0, нормализирано |
1 |
[1…254] |
f |
|
1 |
[1…2046] |
f |
|
|
( +X ) ≠ 0, ненормализирано |
0 |
0 |
≠ 0 |
|
0 |
0 |
≠ 0 |
|
|
( –X ) ≠ 0, ненормализирано |
1 |
0 |
≠ 0 |
|
1 |
0 |
≠ 0 |
|
Забележка: В
таблицата f – означават
всяка
възможна за
полето F стойност.
Последните
два реда от
таблица 1.6 се
нуждаят от
допълнителни
пояснения, тъй
като става дума
за поредната
особеност. Когато в
резултат на
изчисленията
се получи
много малко число,
чиято
мантиса не
може да се
нормализира
във
възможностите
на полето на
порядъка
(характеристиката),
то това
число може да
остане
записано във
вида:
|
S |
H |
HB |
F |
|
0 or
1 |
000 ... 00 |
0 |
000 ...... 001xxxxxx …… xxx |
|
|
|
… … r … … |
|
|
|
|
недостиг от
ниво r |
|
Този
вид се
характеризира
с
отстъпление
от условието
за
нормализирана
мантиса. Неговата
характеристика
е нула (Н=0), мантисата е М<1, а
нейната
дробна част – F≠0.
Такова число
се нарича ненормализирано. Всеки
опит то да
бъде
нормализирано
ще доведе до отрицателно
препълване в
полето на
порядъка. С
други думи
това число е
толкова
малко, че върху
числовата ос
то стои много
по-близко до
нулата,
отколкото до
най-малкото
по модул
представимо
нормализирано
число
![]()
Близостта
на това число до
минималното
представимо
число се измерва
с понятието ниво
на недостиг.
Недостиг от
ниво (r)
означава r незначещи
цифри 0
в старшата
част на
мантисата. Ако
например
дъжината на
мантисата е 8[b],
т.е. m=8, тогава
максималното
ниво за
недостиг за
тази разрядна
мрежа ще бъде
r=m-1=7. Така
в нея ще бъде
възможно за
представяне
следното
число с
нормализирана
мантиса:
![]()
и следните
числа с
ненормализирана
мантиса:
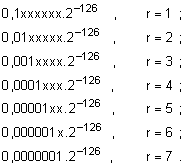
В практическите
реализации
на
разглежданата
форма,
производителите
на
изчислителна
техника
предлагат
различни
решения.
Най-често
ненормализираното
число от този
вид се замества
с машинна
нула, а в
по-универсалните
реализации
на
програмиста
се дава възможност
да провежда
изчисленията
в условия на
недостиг, с
което
точността на
резултатите
се повишава
допълнително.
Когато
в разрядната
мрежа с
плаваща
запетая се
получат
числа,
съответстващи
на последните
два реда от
таблица 1.1.6.2.2, се
говори, че е
настъпило антипрепълване
на
разрядната
мрежа (underflow). А в случаите,
когато се
получи число,
което е
толкова
голямо, че
нормализирането
му води до
положително
препълване в
полето на порядъка,
се говори, че
е настъпило препълване
на
разрядната
мрежа (overflow) или
още препълване
при плаваща
запетая.
Числата,
които могат
да се
характеризират
с тези два
признака,
формират
върху числовата
съответните
области,
които ще
поясним графично,
чрез
рисунката от
фигура 1.1.6.2.5
(аналогично
на фигура 1.1.6.1.4).
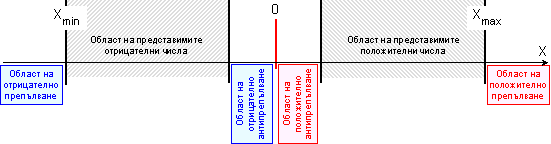
Фиг. 1.1.6.2.5.
Диапазон на
представимите
числа
Двете
най-близки до
нулата
представими
числа
ограничават
областите на
отрицателно
и
положително
антипрепълване
както следва:
·
област
на
отрицателно
антипрепълване:
![]()
·
област
на
положително
антипрепълване:
![]()
Тъй като съществуват
още някои
много важни
особености,
свързани с
тази форма за
представяне
на числата,
които
технологично
все още не са изложени,
тук ще
считаме
темата за
незавършена.
Тези
особености са
свързани с
машинните
кодове на
числата от
една страна и
с
алгоритмите
за извършване
на
аритметични
операции с
тази форма –
от друга
страна. Тези
въпроси
предстоят да
бъдат
изложени, ето защо на
този етап
приемаме, че
някои положения,
свързани с
представяне
на числата
във форма с
плаваща
запетая, все
още не са
окончателно
изяснени.
Изключения
Ще
добавим
обаче още
няколко
понятия, които
са
непосредствено
свързани с
излагания стандарт.
Според
стандарта на IEEE,
ако по време
на
изчисленията
настъпи някоя
от следните
ситуации:
·
Изчезване
на
значимостта (Underflow);
·
Препълване (Overflow);
·
Деление
на нула (Divide by Zero);
·
Определено
е условие неточен
(Inexact) или
невалиден (Invalid) резултат,
·
Недействителна
операция (Invalid Operation) ,
тогава е
предвидено
да се вдигне
допълнителен
флаг
(признак) за
това. Това е
флаг за изключително
събитие.
Маркирането
на тези
събития има
за цел
по-съвършенното
управление
на изчислителния
процес и
по-гъвкавото
използване
на изключителните
стойности.
Inexact е признак,
който
възниква
винаги,
когато за
представяне на
резултата от
дадена
операция в
един от нормалните
формати на
разрядната
мрежа, същият
трябва да
бъде закръглен.
Invalid е признак,
който
възниква
винаги,
когато зададените
операнди
правят
заповяданата
операция недефинирана. Недефинираните
операции са 7:
1.
Деление
нула на нула (0.0)/(0.0);
2.
Корен
втори от
отрицателна
стойност,
например (√-1);
3.
Умножение
нула на
безкрайност
(0.0)*(∞);
4.
Умножение
безкрайност
на
безкрайност
(∞)*(∞);
5.
Изваждане
безкрайност
от
безкрайност (∞-∞),
но само ако
знаците на
операндите
са еднакви.
Обаче
операция
събиране на
безкрайност
с
безкрайност
дава
безкрайност,
когато
операндите
са с еднакви
знаци
(∞+∞=∞);
6.
Функция
за остатък
при делител
нула (REMAINDER(Anything, 0.0));
7.
Функция
за остатък от безкрайност (REMAINDER(∞, Anything)).
Преобразуването
на числа от форма с
плаваща
запетая в
други
форми или
формати
също може да доведе
до условие Invalid,
дори ако не
може да бъде определен
резултат NaN. NaN
не трябва да
се бърка с "Undefined".
Стандартът IEEE-754
дефинира NaN
много добре,
въпреки че
повечето
езикови
стандарти го
игнорират и
много
компилатори
се
отклоняват
от това определение.
При
възникване
на някоя от
споменатите
изключителни
ситуации, на
резултата се
присвоява
някое от
специалните
значения,
които
определихме
по-горе (вижте
таблица 1.1.6.2.2). За
по-голяма
гъвкавост и
поради
възможностите
за тълкуване
на
получените
изключителни
резултати,
възникналите
изключения не
водят
непременно
до
прекъсване
изпълнението
на
програмата, в
която са натъпили.
Те са
“покрити” с
маски за
прекъсване.
Ако по време
на
настъпването
на изключителната
ситуация
флагът за
съответното
прекъсване е
разрешен, то
може да се
извърши прекъсване
с преход към
системна или
към потребителска
програма за
обработка на
съответната
изключителна
ситуация. Ако
флагът не
разрешава
прекъсване,
то
алтернативата
за проверка и
обработка на
изключителните
ситуации
следва да се
съдържа в
потребителската
програма. В
този смисъл
познаването
на
описваните
тук ефекти е
отговорност на
програмиста.
Изключението
например,
наречено “деление
на нула” се
счита от
някои
изследователи
за погрешно
наречено и
исторически
наследено.
Препоръчва
се
наименованието
“неопределен
резултат,
изчислен
точно от крайни
операнди”,
което е в
по-голямо
съответствие
с възможните
числени
резултати. В
подкрепа на
това
наименование
се дава
следния пример
- 3.0/0.0. Според
стандарта IEEE 754 за този
пример
резултатът
по
подразбиране
е
безкрайност.
Знакът на
този
резултат обаче
се определя
от знаците на
операндите чрез
логическата
функция
нееднозначност,
което води до
различни
крайни
резултати (ще
бъдат
коментирани
в глава 3 на
тази книга).
Обръщаме
внимание на
това, че
делението на
нула е
единствената
алгебрическа
операция, която
разкрива
знака на
нулата.
Стандартът
препоръчва
неалгебричната
функция CopySign за
разкриване
на знака, без
да се стига
до изключение,
но не всички
компилатори
я предлагат.
В тази връзка
резултатите
от някои изрази
могат да се
третират по
този начин вместо
да се
класифицират
като грешка
или като недефинирани.
Ако
програмистът
има правилно
отношение,
безкрайните
междинни
резултати
могат да се
превърнат в
правилни
крайни
резултати. В
противен
случай
най-вероятно
безкрайността
ще се
превърне в NaN с
признак INVALID.
За
разлика от
целочисленото
деление с
нула (за
което не е
предвиден
резултат безкрайност
или NaN), делението
с нула във
форма с
плаваща
запетая не е
така фатално
и опасно
(стига да се
уважат
сигналите INVALID, ако се
появят),
което дава
възможност
да се изключи
капана за
деление на
нула.
Изключение
“Overflow” ,
както вече
беше
обяснено,
настъпва
когато
резултатът
излезе извън
възможностите
на
разрядната
мрежа. Кога и
как се случва
това ще бъде
пояснено
по-късно тук
в глава 3, при
представянето
на
алгоритмите
за изпълнение
на
аритметичните
операции. В
такава
ситуаци
стандартът
задължава
хардуера да
апроксимира
резултата и
да го
сигнализира
като
безкрайност (Infinity). Тъй
като е
резултатът е
апроксимиран,
т.е. представен
приблизително,
това
изключение
се
сигнализира
като Inexact.
Тази апроксимация
най-често е
безполезна и
при матрични
изчисления
води до NaN. По
тези причини
ситуацията Overflow попада в
капан.
Изчезване
на
значимостта
(изключение Underflow) е ситуация,
която
настъпва
след опит да
се апроксимира
резултат,
който се
намира по-близо
до
абсолютната
нула,
отколкото
планирания в
стандарта
минимален
резултат (2,2Е-308
във формат Double например).
В хардуерът
се прави опит
да се
закръгли получения
резултат,
който може да
се намира в
интервала от
2,2Е-308 до 4,9Е-324,
когато се
отчита нивото
за недостиг,
за което беше
писано по-горе.
Ако това не
се получи, за
резултат се
приема нула.
Форматите Single и Extended имат други
прагове на
изключението
Underflow. Ако
закръглянето
не генерира
грешка, изключението
Underflow не настъва. И
тези ситуации
ще бъдат
разглеждани
допълнително
в
глава 3, при
представянето
на
алгоритмите за
изпълнение
на
аритметичните
операции.
Ситуацията
Inexact се
сигнализира
винаги,
когато
идеалният резултат
от
аритметическата
операция не се
събира в
определения
му формат. В
този случай
хардуерът
изпълнява
закръгляне.
Това се прави
чрез
споменатата
по-горе
функция round(X,v). Самата
функция и
нейната
апаратна
реализация в
устройствата
за работа с
плаваща запетая
ще бъде
изяснено допълнително
в
глава 3.
Капанът Inexact е маскиран
в почти целия
софтуер с
плаваща запетая,
но
перфекните
програмисти
биха могли да
го използват
при
постигане на
по-висока
точност.
В
научните
публикации
читателят би
могъл да
намери много
полезни
съвети за
използване
на тези
изключения.
Такива има и
те са
различни в
отделните
езици и
техните
компилатори.
Обемът на
тази
информация не
е никак малък
и във висока
степен касае
софтуера,
който ние тук
не
коментираме.
Следващият
раздел е:
1.1.6.3
Двоично-десетични
числа (BCD) ( Binary code decimal )