1.1.6.3 Двоично-десетични числа (BCD)

Binary code decimal

Специално внимание производителите на изчислителни устройства отделят на представянето на десетичните числа, с което се поддържа по-непосредственото общуване на човека с изчислителното устройство, като се има предвид неговата оценъчна система, построена изцяло върху понятията на десетичната бройна система. Ето защо в групата на числовите данни самостоятелно значение имат двоично кодираните десетични числа, наричани просто двоично-десетични. Често така кодираните числа се наричат BCD-числа (BCD – Binary Code Decimal). Имитацията за числото 268,47 може да изглежда например така:

268,47 º 0010 0110 1000 , 0100 0111

Може да се каже, че представянето на десетичните цифри чрез техните двоични кодови комбинации, е своеобразна имитация на десетичните числа с машинни средства.

Двоично-десетичните числа се представят най-често във форма с фиксирана запетая, т.е. като последователност (низ) от двоични кодове на десетичните цифри на числото. Естественият произход на този низ обикновено е процес на въвеждане на данни от клавиатурата. Предвид на аритметичните операции, които се извършват с тези числа, въпросът за двоичното кодиране на десетичните цифри ще бъде разгледан по-надолу. Що се отнася до форматите за съхраняване на двоично-десетични числа, те са два: непакетиран и пакетиран.

Непакетираният формат представя десетичното число като последователност от кодовете на отделните цифри, знак, десетичен разделител (,) и др., според кодовата таблица на използвания стандарт, т.е. съществуват като символен низ. При това положение младшите 4 бита на символния код представляват кода на десетичната цифра. Така например число 7095, според ASCII таблицата ще има следния непакетиран формат:

0011	0111	0011	0000	0011	1001	0011	0101
КЗ		КЗ		КЗ		КЗ
	7		0		9		5

където КЗ означава ASCII-код на зоната. В този формат обикновено числата съществуват непосредствено след тяхното въвеждане от клавиатурата или преди непосредственото им визуализиране на екрана на монитора.

Пакетираният формат на едно двоично-десетично число представлява последователност от 4-битови двоични кодове на неговите цифри. Например горното число 7095 може да се представи в пакетиран формат чрез последователността: <cd7><cd0><cd9><cd5>, която се побира в поле с дължина 2[B], т.е. всеки 4 бита представляват код на десетична цифра (cd). Когато двоично-десетичното число се представя като число със знак, последният се кодира с 4-битова кодова комбинация, несъответстваща на десетична цифра. Пакетираният формат е удобен и като вътрешно-машинен при непосредственото обработване на двоично-десетичните числа. От гледна точка на обработването обаче знакът на числото може да се представя от десетична цифра.

Форматите на двоично-десетичните числа, за които стана дума по-горе, не са пряко свързани с форматите на разрядната мрежа на процесора, тъй като десетичната бройна система не е основна (не е оптимална) бройна система.

Кодиране на десетичните цифри

Ако приемем, че символите на десетичните цифри се кодират в двузначна система, то минималната дължина на техния код се определя по формулата

При тази дължина на кода са възможни 16 уникални двоични комбинации, т.е. този набор съдържа неотстраним излишък от 6 комбинации. В пункт 1.1.3 споменатите комбинации бяха наречени тетради. За да се създаде код, с чиято помощ да се изразят десетичните цифри, е необходимо да се декларира съответствието на всеки един от десетичните символи към една от 16-те възможни двоични комбинации. Задачата за създаване на код в изказания смисъл (избор на 10 елемента измежду 16) се изразява чрез формулата за броя на биноминалните коефициенти:

С други думи, изчислената стойност представлява общия брой 4-битови двоично-десетични кодове, които могат да бъдат създадени при горните условия. Това количество усложнява много сериозно задачата за избор на удобен и приложим 2/10-чен код.

Тук обаче става въпрос не само за кодиране на символите, с помощта на които ще бъдат изобразявани такива символни низове, които ние определяме като числа. А както знаем, числата влизат помежду си в много сложни операции, ето защо не е без значение как е съставен изобразяващият десетичните цифри код. Естествено е разбирането, че кодът на десетичните цифри следва да бъде съставен така, че да облекчава техническата реализацията на аритметичните операции. Резултатите от изследванията върху този проблем тук ние ще изложим крайно ограничено.

Съставеният за целите на двоично-десетичните изчисления код на десетичните цифри в светлината на изложеното по-горе разбиране е желателно да притежава следните пет свойства, наричани изисквания на Рутисхаузер:

1. Еднозначност. Съответствието между кодовата комбинация и десетичната цифра трябва да бъде еднозначно. Ако това е изпълнено, става възможно да се оперира с двоично-десетично кодирани числа, при това декодирането е ефективно.

2. Монотонност. Според това свойство, на цифри, означаващи по-голямо елементарно количество, се полага код, който може да се интерпретира като по-голямо двоично число (или противоположното). Такова съотношение способства за по-лесно реализиране на операция сравнение.

3. Четност. На четни десетични цифри трябва да съответстват четни двоични комбинации (или противоположното). Свойството четност спомага за извършване на правилно десетично закръгляне и спомага за по-голяма простота при изпълнение на операция деление.

4. Допълняемост. Това свойство е в сила, ако във всяка сума от две десетични цифри, която е равна на максималната цифра

,

цифрите са кодирани с такива тетради, че едната може да бъде получена от другата чрез поразрядна инверсия. Това свойство способствува синтеза на допълнителен и обратен код на числата със знак.

5. Тегловна значимост. Според това свойство елементарното количество, означено с дадена десетична цифра, трябва да се получава от двоичния код като сума от теглата на позициите, в които има значеща цифра:

където

са двоичните цифри на кодовата комбинация, а

са приписаните тегла на позициите в кодовата комбинация под съответния номер. Това свойство облекчава логиката на операциите между двоично-десетичните числа, както и декодирането на числата.

Известни са задълбочени изследвания, имащи за цел откриването на кодове, удовлетворяващи всички посочени изисквания на Рутисхаузер. Тук ще бъдат посочени само някои резултати от тези изследвания, отнасящи се до кодове, които изпълняват някои от тези изисквания, тъй като не е известен код, който да ги удовлетворява всичките. Съставянето на код за десетичните цифри обикновено се извъзшва като някои от посочените изисквания на Рутисхаузер се игнорират.

Така например, ако се комбинират изискванията за еднозначност с тегловна значимост и при това се приеме, че кодът е с положителни тегла, т.е.

то може да се докаже, че, за да притежава кодът свойството допълняемост, е необходимо и достатъчно десетичната цифра 9 да се кодира с двоичната комбинация 1111. С други думи, сумата от теглата на позициите трябва да бъде равна на девет:

Твърдението се доказва така:

Ако се приеме, че предварителното условие е изпълнено и за някоя десетична цифра di е съставена кодовата комбинация <b3 b2 b1 b0>, то за цифрата, съответстваща на разликата (9-di) е в сила изискването за допълняемост. Проверяваме това твърдение непосредствено

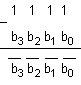
където двоичната разлика представлява поразрядната инверсия на кодовата комбинация, с което твърдението е доказано.

Всички кодове, които притежават едновременно свойствата монотонност, тегловна значимост (при положителни тегла на позициите) и допълняемост, са посочени в таблица 1.1.6.3.1.

Таблица 1.1.6.3.1

№
1	5 2 1 1
2	4 3 1 1
3	4 2 2 1
4	3 3 2 1

Ако се допусне, че една от позициите на кода може да приеме отрицателно тегло, то може да се твърди, че само 14 кода притежават свойството еднозначност. Тези кодове са представени чрез теглата си в таблица 1.1.6.3.2.

Таблица 1.1.6.3.2

№
1	8 4 3 -6
2	8 6 1 -4
3	8 4 2 -3
4	8 2 1 -4
5	8 5 2 -4
6	8 4 2 -1
7	8 4 3 -2
8	8 4 1 -2
9	8 4 2 -5
10	8 3 2 -4
11	8 4 1 -6
12	7 6 3 -5
13	7 5 3 -6
14	6 5 3 -7

От посочените в таблицата кодове, само 4 притежават и свойството допълняемост – това са кодовете под номер 1, 9, 10 и 13. От тези четири кода само един притежава освен изброените свойства (тегловна значимост, еднозначност, допълняемост), още едно – четност. Това е кодът под номер 9 – (8 4 2 -5). За съжаление нито един от кодовете не притежава свойството монотонност.

Може да се докаже, че, за да се въведе тегловно значим код с дробни стойности на теглата, е необходимо да се увеличи дължината на кодовата комбинация. С други думи се твърди, че при дължина на кодовата комбинация 4[b] могат да се построят кодове само с целочислени тегла.

Ако теглата на позициите са положителни, то може да се покаже, че единственият код, който притежава безусловно свойството еднозначност, е кодът на прякото заместване (8421).

От кодовете с положителни тегла само два кода удовлетворяват най-добре изискванията на Рутисхаузер – кодовете (4221) и (2421), които са известни под името кодове на Емери. Тези кодове не притежават свойството еднозначност. Ако обаче се приеме като безусловно или първично свойството допълняемост, то комбинациите, получаващи се в повече, могат да бъдат приети за забранени и тогава, при това условие, може да се приеме, че кодът притежава и свойството еднозначност. Така например кодът (4221) има следните възможни комбинации:

Таблица 1.1.6.3.3

	4 2 2 1
№	основни	забранени
0	0 0 0 0
1	0 0 0 1
2	0 1 0 0	0 0 1 0
3	0 1 0 1	0 0 1 1
4	0 1 1 0	1 0 0 0
5	1 0 0 1	0 1 1 1
6	1 0 1 0	1 1 0 0
7	1 0 1 1	1 1 0 1
8	1 1 1 0
9	1 1 1 1

Съвкупността от основни комбинации за цифрите 2, 3, 4, 5, 6, 7 е взаимозаменяема със съвкупността от забранени комбинации, но само за основните е в сила и свойството допълняемост, и свойството четност, и свойството монотонност. При използване на тези кодове забранеността или още невъзможността да се явяват посочените комбинации следва да се осигури с технически средства.

Съществува още една група двоични кодове, които притежават забележителни свойства, свързани с простота при изпълнение на аритметичните операции върху числа, записани с тяхна помощ. Едни от най-прилаганите са така наречените кодове с излишък относно кода на прякото заместване (8421). Формулата на тяхното получаване е сумата (8421)+C, където С е константа, формираща всяка кодова комбинация след означената операция.

Известно е, че всички кодове с излишък равен на 7 и по-голям от 7 (C7), не притежават свойството монотонност. Тези, които са с излишък по-малък от 7 (C<7), притежават свойствата еднозначност, четност и монотонност, но само един от тях (кодът с излишък три, C=3) притежава свойството допълняемост. Свойствата на кодовете с излишък са тясно свързани с тези на кодовете, имащи отрицателни тегла.

Последните два кода – кода на прякото заместване (8421) и кода с излишък (+3) ще бъдат обект на допълнително разглеждане, предвид на тяхното най-често използване. Това читателят може да види в книга [2], където е представен логическият синтез на 2/10-чни суматори на числа, чиито цифри са кодирани с тези кодове. Там са представени и числени примери за аритметическите операции с такива числа.

Следващият раздел е:

§ 1.2 Операция аритметическо събиране ( Operation arithmetic summation )