§ 1.2 Операция аритметическо събиране

Operation arithmetic summation

Ако се приеме, че за представяне на числата в разрядната мрежа е избрана една бройна система, това означава, че са в сила и правилата за извършване на аритметическите операции, дефинирани в нея. Известни са четири аритметически операции върху числови данни, от които операция събиране е основна, а останалите три – изваждане, умножение и деление се определят чрез нея. Когато става дума за позиционна бройна система, правилата за аритметическо опериране се дефинират с таблицата за събиране на елементарни количества. Операция аритметическо събиране е двуместна операция и тук ще бъде означавана така X+Y=Z. Тя има два операнда X и Y. Резултатът Z се нарича сума. Когато операндите са числа без знак, тя е винаги възможна. Непосредствената реализация на операция събиране се осъществява апаратно от логическа схема наричана суматор. Техническата реализация на този логически възел е подробно представена в книга [2].

Тук ще продължим да се занимаваме с представяне на данните, но при това ще намесим и правилата за опериране, на които се основава техническата реализация на суматора. Това е наше първично задължение, следствие от гледната точка и разбиране, изложени в предговора към тази книга. Оперирането трябва да бъде разгледано, тъй като е неотменна част от понятието бройна система (вижте определението в пункт 1.1.1).

Две многоразрядни числа без знак се събират по определение поразрядно, започвайки от младшите цифри на операндите X, Y, последователно към старшите, въз основа на полиномния им запис (1.1.4):

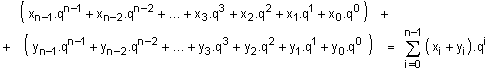
при n битова разрядна мрежа.

Известно е, че анализът на сумата от съответните коефициенти на полиномите изявява два поразрядни резултата – функция на сумата z_i и функция на преноса p_i.

Всяка цифра z_i на многоразрядната сума Z се получава по един и същи начин, определен от дефиниращата таблица, като сума S от цифрите на събираемите x_i, y_i и преноса от съседния по-младши разряд p_i-1. Тъй като тази сума не винаги представлява елементарно количество, освен цифрата z_i, в текущата позиция се определя и стойността на преноса p_i, възникващ в нея. Този пренос подлежи на разпространение в съседната, по-старша позиция с номер (i+1).

Операция събиране на две многоразрядни числа, описана по този начин, може да се определи аналитично със следната система уравнения:

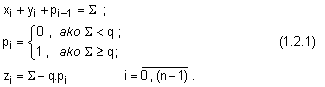
където с n е означена дължината на разрядната мрежа.

Както беше отбелязано по-горе, техническото средство, материализиращо операция събиране, изразена чрез системата (1.2.1), се нарича суматор. За разлика от множеството примери за построяване на такова средство, дадени в краткия исторически преглед в началото на тази книга, тук ние се интересуваме само от онези технически средства, които притежават основното качество високо бързодействие. В съвременни условия това качество на техническите средства се осигурява чрез използване на най-бързото познато на човека физическото явление, което се нарича електрическо поле. Практическата реализация на суматора като електронна логическа схема се постига с помощта на методите на логическия синтез. С методите за синтез на този основен логически възел в най-разнообразните му форми на изпълнение читателят може да се запознае в книга [2].

От системата (1.2.1) се вижда, че при събиране на две n разрядни числа без знак, сумата може да надхвърли възможностите на разрядната мрежа, т.е. да се получи препълване. Този факт се открива чрез стойността на преноса от най-старшия разряд. Ако p_n-1=1, оставащата в разрядната мрежа последователност от цифри

( z_n-1 z_n-2 z_n-3 …… z₂ z₁ z₀ )

не представлява резултата, а само неговите n младши цифри. Истинският резултат е разширен отляво с още една позиция, в която стои стойността на преноса p_n-1, т.е. сумата е (n+1) разрядното число:

( 1 z_n-1 z_n-2 z_n-3 …… z₂ z₁ z₀) ,

както е показано на примера:

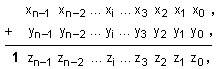
Препълването на разрядната мрежа при събиране на числа без знак следователно може да бъде само отдясно, т.е. само положително (вижте фигура 1.1.6.1.4). Резултатът (сумата) при препълване се удължава отляво, но само с една позиция, в която стои цифрата 1 (независимо каква е основата q на използваната бройна система).

Възникващият от най-старшия разряд на разрядната мрежа пренос обикновено се запомня в допълнителен разряд, означаван специално с буквата C (от думата carry – пренос). По този начин получената сума не е загубена дори и в случай на препълване. Въвеждайки този допълнителен разряд на сумата, става възможен за реализация паралелно-последователният метод за събиране на числа с по-голяма дължина от тази на разрядната мрежа. Трябва да се подчертае, че този разряд не е част от разрядната мрежа. Тази особеност на операция събиране ще бъде подробно пояснена в последствие с представянето на аритметично-логическото устройство на цифровата машина.

За индициране на ситуацията препълване на разрядната мрежа се въвежда друг специален признак на резултата, означаван с буквата V (втората буква на думата overflow – препълване). Признакът за препълване се кодира с логическите стойности както следва:

При събиране на числа без знак, логическата функция, която дава стойност на този признак, има вида:

Следващият раздел е:

§ 1.3 Операция аритметическо изваждане ( Operation arithmetic subtraction )