§ 1.3 Операция аритметическо изваждане

Operation arithmetic subtraction

Операция аритметическо изваждане е двуместна операция и има два операнда: X – умаляемо; Y - умалител. Резултатът Z се нарича разлика и се определя чрез операция събиране, т.е. разликата е такова число, чиято сума с умалителя е равна на умаляемото. Операцията е двуместна и тук ще бъде означавана така X–Y=Z. Когато операндите са числа без знак, операция изваждане е не винаги възможна. За разлика от предходната операция, в общия случай тази може да доведе до резултат, който е число със знак, например (3-5=-2). Изпълнението на операция изваждане върху две многоразрядни числа е определено аналогично на това при операция събиране, като поразрядно:

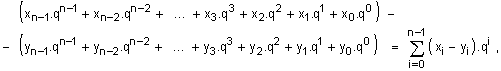
което се изпълнява в съответствие с дефиниционната таблица на елементарните количества. Известно е, че анализът на разликата от съответните коефициенти на полиномите изявява два поразрядни резултата – функция на разликата z_i и функция на заема q.p_i.

Изваждането на елементарни количества, както и на многоразрядни числа е определено като операция само при условие, че е изпълнено неравенството

| X | ≥ | Y | (1.3.1)

Ето защо, дори когато операндите са числа без знак, разликата следва да се приема като число със знак, което дава известни основания операцията да се нарича в общия случай алгебрическа. Ако модулът на умаляемото е по-голям от модула на умалителя, т.е. когато условие (1.3.1) е изпълнено, изваждането се извършва според дефиниращата таблица на бройната система – изваждане на модулите |X|–|Y|, в резултат на което в разрядната мрежа се получава модулът на разликата |Z|, т.е. изпълнението е по определение. Само в този случай резултатът може да се интерпретира по-нататък като число без знак, тъй като Z>0.

Когато модулът на умаляемото е по-малък от този на умалителя |X|<|Y|, операцията не е определена, т.е. резултатът като число без знак не съществува. Според правилата за алгебрическо изваждане обаче, операндите могат да сменят местата си и да се извърши изваждането |Y|–|X| по определение, като при това полученият резултат следва да се разглежда като число със знак минус, т.е. Z<0.

И в двата случая на изваждане може да се твърди, че модулът на разликата |Z|, е по-малък от модула на по-големия операнд (разглеждан като число без знак). Това означава, че модулът на разликата е представимо в разрядната мрежа число, т.е. препълване не е възможно да настъпи. Това определя при изваждане на числа без знак признакът V да има стойност нула V=0.

Ако изваждането обаче не се извършва с предварителен анализ на съотношението на модулите, в случай на отрицателен резултат, може да се говори за препълване отляво, т.е. за отрицателно препълване, което обаче е безсмислено в контекста на числата без знак. Какво все пак се получава в разрядната мрежа? Ако е било в сила неравенството |X|³|Y|, в разрядната мрежа ще остане |Z|, който следва да се интерпретира като положително число. Ако е било в сила обаче неравенството |X|<|Y|, в процеса на изваждане при формиране на цифрата на разликата, в позицията на най-старшата значеща цифра на умаляемото или от съседната по-старша позиция, ще бъде поискан заем, който е от разряд извън разрядната мрежа, т.е. от разряда C. В този смисъл, при операция изваждане на числа без знак, разрядът C ще отбелязва възникването на заем вън от разрядната мрежа. Този факт може да се използва при изваждане на дълги числа (аналогично на операция събиране) чрез паралелно-последователния метод на обработка.

В случай на изваждане на представими в разрядната мрежа числа и отрицателна разлика, оставащата в разрядната мрежа последователност от цифри не е модулът на очаквания резултат.

Например, ако изваждането (0023–0047) се извърши с предварително сравнение на модулите и смяна на местата на операндите, ще бъде изпълнена операцията (0047–0023), която ще даде модула на резултата: 0024. Истинската разлика е числото Z=–24, чийто знак следва да бъде съобразен логически. Ако обаче се пристъпи към изваждане без смяна на местата на операндите, ще се получи следният резултат:

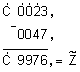
където последователността

,

т.е. не е модулът на резултата, а в бит C е фиксиран заем, което по-горе в примера, е означено с точка. След няколко подобни примера лесно може да се обобщи, че получената при това изпълнение на операцията последователност

,

е допълнението на модула на търсената разлика |X-Y| до числото qⁿ (в примера 10⁴ = 10000). И наистина

Тези съждения обосновават възможността да бъде получен истинският модул на разликата, ако се реши спрямо неизвестния модул следното уравнение

От казаното се разбира, че техническото реализиране на операция изваждане по определение е значително по-сложно. Посочените й особености обаче показват, че вероятно има път към нейното опростяване и този път ще бъде подробно разгледан по-късно.

Следващият раздел е:

§ 1.4 Операция умножение и операция деление ( Operation multiplication and operation division )