1.6.2
Представяне
на числата в
допълнителен
код
Twos
complement representation
Търсенето
на удобен код
за
представяне
на числата
със знак в
разрядна
мрежа с
ограничена
дължина води
до идеята за
представяне
на числата по
модул,
основаваща
се на понятието
сравняване
на числата по
модул,
определено в
теорията на
числата. За
това ние ще
пишем
значително
по-подробно в
раздел 3.3.5.3
на тази
книга.
Тук
ние няма да
се впускаме в
детайлно
излагане на
елементи от
тази теория,
но любознателният
читател може
да намери
строго
математическото
потвърждение
на
изложеното
по-долу в
разделите,
отнасящи се
до крайните
комутативни
пръстени с
единица,
определени
като полета
на Галуа (Galois E.).
Две
натурални
числа X1 и X2, (X1,X2Î![]() )
се наричат сравними
(съпоставими)
по модул M (modM),
ако при
целочисленото
деление X1/M и X2/M
се получават
еднакви
остатъци.
Това
определение можем
представим
така:
)
се наричат сравними
(съпоставими)
по модул M (modM),
ако при
целочисленото
деление X1/M и X2/M
се получават
еднакви
остатъци.
Това
определение можем
представим
така:
![]()
където с R е
означен
споменатият
остатък, а с s1, s2
са означени
целите
частни, които
показват
кратността
на модула в
изходните
числа.
Остатъкът е
общ и според
(1.4.5) може да
бъде изразен
по следния
начин:
![]()
Сравнимостта (еквивалентността) в смисъла на модула М на двете числа се записва така:
![]()
или
още така:
![]()
където
M е
положително
число.
От
определението
следва, че
модулът за
сравнимост M
разделя
множеството
натурални
числа ![]() на M на
брой
непресичащи
се
подмножества
на M на
брой
непресичащи
се
подмножества
![]()
наричани остатъчни
класове.
Елементите
на
остатъчните
класове са
натурални
числа, кратни
помежду си на
модула M, т.е.
![]()
Например,
ако R=2, при modM=3,
подмножество
![]() ще
съдържа
числата 5, 8, 14, 17, 20, 23,
, и т.н., т.е.
всяко от
подмножествата
е безкрайно.
Така, на
основание на
еднозначното
съответствие
между
остатъците R и
класовете
ще
съдържа
числата 5, 8, 14, 17, 20, 23,
, и т.н., т.е.
всяко от
подмножествата
е безкрайно.
Така, на
основание на
еднозначното
съответствие
между
остатъците R и
класовете
![]()
възниква
идеята за
използване
на остатъка R
като изображение
(код) на
числата от
съответното
подмножество.
Естествените
задачи, които
възникват от
тази идея са
две:
·
Права
задача,
при която е
известно
числото X и се
търси изображението
му R ;
·
Обратна
задача,
при която е
известно
изображението
R и се търси
числото X.
Ще поясним, въз основа на определението, решенията на формулираните задачи с помощта на рисунката от фигура 1.6.2.1.
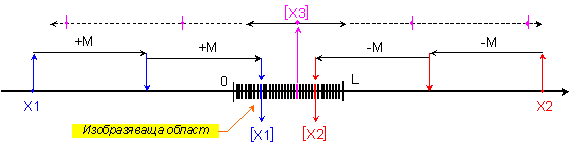
Фиг. 1.6.2.1.
Схема за
решаване на
правата и
обратната
задача
От рисунката е очевидно, че правата задача може да се реши чрез последователно изваждане на модула за сравнение М от даденото положително число X2, докато се получи разлика, която попада в изобразяващата област. При това ще въведем следното означение за изображението (за кода)
X1(modM) = R1 = [X1] ; X2(modM) =
R2 = [X2] . (1.6.2.4)
Вижда се, че когато числото X1 е отрицателно, движението в посока на изобразяващата област се постига с положителни стъпки. Вижда се още, че квадратните скоби означават изображението (кода), а не самото число.
Необходимо е да изтъкнем, че изображението на всяко цяло число трябва да бъде единствено. Това е възможно само когато дължината L на изобразяващата област е на единица по-малка от модула за сравнимост М, т.е. L=М-1.
Ако L>(М-1), то ще има числа, за които могат да бъдат определени повече от едно изображения, т.е. правата задача има неединствено решение. А ако L<(М-1), то ще има числа, които не могат да бъдат изобразени, т.е. в този случай правата задача не винаги има решение.
Обратната
задача има
безкрайно
много решения.
Както е показано
на фигура 1.6.2.1,
кодът R3=[X3] е
изображение
на
елементите
на остатъчен клас
![]()
които са
разположени
в двете
посоки на числовата
ос. От тях
може да бъде
избрано едно
конкретно решение,
само ако се
посочи
съответстващата
му степен на кратност.
Например, ако
се търси
положително
число със
степен на
кратност s, то
по
определение
решението е X3=[X3]+s.M.
В случай, че
се търси
отрицателно
число, решението
е X3=[X3]s.M.
Тук ще
напуснем
общата
теория и ще
разгледаме
нейното приложение
в
специфичните
за нас
условия. Нека
припомним, че
мястото за
представяне
на изображението
(кода) на едно
число, е
разрядната
мрежа. При дясно
фиксирана
запетая и
дължина от n разряда, броят на
представимите
в нея
комбинации (числа) е
![]()
Числото
(1.6.2.5) се нарича модул на
разрядната
мрежа.
Неговата
дължина е (n+1)
разряда, а
видът му е
единица с n
младши нули,
както е
показано на
следващата
рисунка
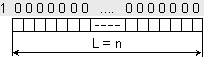
Фиг. 1.6.2.2.
Положение
на модула на
разрядната мрежа
Този вид на модула на разрядната мрежа (1000...00) не зависи нито от основата на бройната система q, нито от организацията на разрядната мрежа, т.е. от положението на запетаята (ляво или дясно фиксирана). При двоична разрядна мрежа с дължина n[b], броят на представимите в нея двоични комбинации е N=2n. Всяка една от възможните двоични комбинации може да се приеме за изобразяващ код на съответното число, според таблица 1.6.2.1.
Таблица 1.6.2.1
Кодово
съответствие
|
комбинация |
число
R |
|
000 ...
000 |
0 |
|
000 ...
001 |
1.d |
|
000 ...
010 |
2.d |
|
000 ...
011 |
3.d |
|
-
- - - - - - - - |
-
- - - - - |
|
111 ...
101 |
(N-3).d |
|
111 ...
110 |
(N-2).d |
|
111 ...
111 |
(N-1).d |
където
с d е
означен
дискретът на
разрядната
мрежа. Стойността
на дискрета
се определя
от организацията
на
разрядната
мрежа според
(1.1.6.1.4). Продължавайки
интерпретацията,
можем да приемем
тези числа за
разположени
върху числовата
ос, както е
показано на
следващата
рисунка:

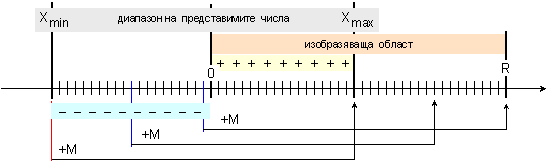
Фиг. 1.6.2.3.
Изобразяваща
област
Така
върху
числовата ос
се отделя
област, която
беше именова изобразяваща
(вижте фигура
1.6.2.1). Дължината
на тази
област е L=(N-1).d. В
частност,
когато
разрядната
мрежа е с дясно
фиксирана
запетая,
дискретът е
равен на
единица (d=1) и
тогава L=N-1. При
това положение,
всяка
комбинация
от таблица 1.6.2.1
представлява
изображение [X].
Според
зависимостта
(1.6.2.3) можем да
запишем, че
![]()
В същото
време от
таблица 1.6.2.1
можем да
запишем, че
![]()
което
довежда до
следното равенство:
![]()
От
последното
равенство (1.6.2.6)
следва много
важното
заключение,
че модулът за
сравнимост M
е равен на
модула на
разрядната
мрежа N. От тук
следва, че R=N-1=М-1,
което
означава, че
за да бъде
изпълнено
условието за
единственост
на
изображението
от таблица 1.6.2.1 в
смисъла на (1.6.2.1),
за негов
модул следва
да се избере
модулът на
разрядната
мрежа, т.е.
![]()
В случай, че разрядната мрежа е с ляво фиксирана запетая, така полученият резултат има следния вид:
![]()
Това,
което все още
обаче не сме
изяснили, е изобразяването
на
отрицателните
числа. Съответствието
на кодовите
комбинации
(като
съдържание
на
разрядната
мрежа), което
таблица 1.6.2.1
пояснява, се
отнасяше до
определението
на понятието
сравнимост
(1.6.2.3).
Необходимо е
да се
установи
ново
съответствие,
което да свързва
кодовите
комбинации с
множеството
на
представимите
в разрядната
мрежа числа
със знак, т.е.
с
определенията
(1.1.6.1.2) и (1.1.6.1.3).
Недостатъкът
на интерпретираното
до този
момент
определение
се състои в
това, че едно
и също
изображение
се поставя в
съответствие
на две
еднакви по
модул, но
различни по
знак числа.
Нещо повече,
от гледна
точка на
кратността,
тези двойки
са безкрайно
много.
Казаното е
илюстрирано
на рисунката
от фигура 1.6.2.1.
Работейки
с
изображенията
на числата,
на нас ни се
налага да
съдим за
самите числа,
което
означава, че
ние ще трябва
да решаваме еднозначно
както
правата, така
и обратната задачи
на
сравнимостта.
Тъй като
обратната
задача няма
еднозначно
решение,
безусловно
се налага да
въведем
ограничение,
като се откажем
от
кратността s, (s=0) и
приемем да
разглеждаме
само числата,
възможни за
изобразяващата
област. Така
излиза, че
възможните
за
изобразяване
положителни
числа са
тези, които
съвпадат с
изображението
си, т.е. +X=[X] и
[X]=+X.
Що
се отнася до
отрицателните
числа, те ще намират
своето
изображение
по
определение,
а именно [X]=X+M. Така, след
всичко
казано, става
възможно да
запишем
формалното
определение
на изобразяващия
код:
![]()
Представяйки
отрицателното
число X чрез знака
и модула му X=-|X|, горната
формула
приема
по-известния
си вид:
![]()
Така
определеното
за
отрицателните
числа
изображение
дава името на
кода допълнителен
код, тъй
като в този
случай той
допълва
модула на
числото до
модула на
кода, т.е.
![]()
За числа в двоична бройна система горното определение приема вида:
·
За числа
с дясно
фиксирана
запетая:
![]()
·
За числа
с ляво фиксирана
запетая:
![]()
Графичното
съответствие
на
положителните
и на
отрицателните
числа спрямо
така определения
код е
представено
чрез фигура 1.6.2.4.
Фиг. 1.6.2.4.
Схема за
определяне
на
допълнителния
код на
числата със
знак
Използвайки
това
графично
представяне
(фигура 1.6.2.4) на
определението
(1.6.2.9), можем да
запишем точното
и единствено
число,
съответстващо
на дадена
n-битова
кодова
комбинация в
разрядната
мрежа.
Съответствието
е
представено
в таблица 1.6.2.2.
Таблица
1.6.2.2 Кодово
съответствие
|
комбинация |
число |
|
000 ...
000 |
0 |
|
000 ...
001 |
+1.d |
|
000 ...
010 |
+2.d |
|
000 ...
011 |
+3.d |
|
-
- - - - - - - - |
-
- - - - - |
|
011 ...
111 |
|
|
100 ...
000 |
|
|
-
- - - - - - - - |
-
- - - - - |
|
111 ...
101 |
-3.d |
|
111 ...
110 |
-2.d |
|
111 ...
111 |
-1.d |
От таблица 1.6.2.2 могат да се направят няколко важни извода:
1.
На първо
място следва
да отбележим,
че между
отделните
комбинации и
числата има
едно единствено
съответствие.
Специално ще
отбележим, че
числото нула
съответства
на
комбинация
нула 000...00.
2.
На второ
място
отбелязваме,
че броят на
положителните
числа, които
заемат
първата половина
на кодовата
таблица, е
равен на броя
на
отрицателните
числа, които
заемат
втората
половина на
кодовата
таблица.
3.
Важно е
да помним, че
в
допълнителен
код, старшите
незначещи
цифри на
числото, с
които се
допълва
цифровата
част на
разрядната
мрежа, съвпадат
с цифрата на
знака, т.е.
ако числото е
положително,
те са нули, а ако
е отрицателно
единици.
4.
При това
разделяне на
комбинациите
в таблицата
се вижда, че
старшата
цифра на
всяка комбинация
съответства
на знака на
числото
което
изобразява,
ако е в сила
кодировката
(1.6.1). Въпреки, че
нямаме право
да правим
това, често
ще наричаме
този бит от
кода знаков.
5.
Диапазонът
на
представимите
в допълнителен
код числа
![]()
се
определя
както следва:
![]()
6.
Диапазонът,
определен с
(1.6.2.13) не е
симетричен
относно
числото нула,
а е удължен с
една стъпка d
в
отрицателна
посока на
числовата ос.
7.
Диапазонът
на
представимите
в допълнителен
код числа
може да бъде
изразен чрез
модула на
разрядната
мрежа N както
следва:
![]()
След
като
пояснихме
смисъла на
понятието сравнимост
(съпоставимост)
на числата и
свързаните с
него
допълнителни
резултати,
формално
дефинирахме
допълнителен
код и
изяснихме
неговите
свойства, следва
да заявим, че съществен
практически
интерес за
нас тук
представлява
въпросът как
тези резултати
ще
способстват
за
изпълнението
на
поставените
в §1.2 и в §1.3 задачи.
Читателят навярно
се досеща, че
ще се търси
еднозначно съответствие
между
резултатите
от операции
събиране и
изваждане,
получени
върху числата
от една
страна и
резултатите
получени
върху
изображенията
на същите
числа, от
друга страна.
Тук
е мястото да
отбележим, че
в теорията на
едномодулната
аритметика
са в сила
теореми,
които
доказват
важни за нас
в момента твърдения.
Например, ако
числата a, b и c
принадлежат
на
множеството ![]() , то са в
сила следните
свойства:
, то са в
сила следните
свойства:
·
комутативност:
![]()
·
асоциативност:
![]()
·
дистрибутивност:
![]()
·
единственост
на 0 и на 1:
![]()
Освен тези теореми особено ценни са още теоремите, утвърждаващи, че:
·
изображението
на сумата от
изображенията
е равна на
изображението
на сумата от
числата:
![]()
·
изображението
на
произведението
от изображенията
е равно на
изображението
на произведението
от числата:
![]()
Аналогично
на казаното в
§1.2 и в §1.3 за
правия код
(кодиране и
опериране),
така и за
допълнителния
код следва да
изясним до
край
въпросите
свързани с
оперирането.
Още веднъж ще
припомним, че
според
постановката
на задачата
ние оперираме
с кодовите
комбинации
на числата,
но желаем по
тях да съдим
за самите
числа.
Решението на
тази задача
се дава от
теорема (1.6.2.17).
Тъй като
нейното
значение е
фундаментално
и изцяло
определящо
техническата
реализация
на цифровите
изчисления
въобще, ние
ще
представим
тази теорема
и нейното
доказателство,
а така също и
получените следствия,
с подобаващо
внимание.
Теорема за събиране
в
допълнителен
код \ (1.6.2.17)
Ако две
числа X и Y, са
представени
от своите
изображения
в разрядна
мрежа с фиксирана
запетая, т.е.
са
представени
в
допълнителен
код
![]()
то е в
сила
твърдението,
че
![]()
при
условие, че
при
събирането
не е настъпило
препълване.
Забележка:
Понятието
препълване и
неговото
означаване
беше
дефинирано в
раздел 1.1.6.1.
Доказателство:
Доказателството
е свързано с
възможните ситуации,
които могат
да се
получат,
разглеждайки
знака на
резултата в
комбинация
със знаците
на
операндите.
Така от тази
гледна точка
могат да се
изявят
четири
ситуации, които
са
разгледани
по-долу.
По
същество
доказателството
непрекъснато
интерпретира
получаваната
кодова сума
![]()
поради
което за
читателя ще
бъде полезно
да наблюдава
рисунката от
фигура 1.6.2.3.
Случай I.
Известно е,
че X>0 и Y>0.
Следователно X+Y>0.
В
този случай
![]()
Така в
разрядната
мрежа се
събират две
кодови
комбинации
от първата
половина на
кодовата
таблица 1.6.2.2.
Ако кодовата
сума S
остане в
зоната за
изобразяване
на положителните
числа (вижте
фигура 1.6.2.3), т.е.
ако S<N/2, то
твърдението
на теоремата е
вярно.
Резултатът
от такова
събиране
може да се представи
както следва:
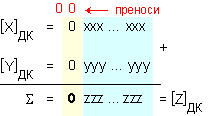
и тогава
можем да
запишем
![]()
Ако
обаче
кодовата
сума S
премине в
зоната за
изобразяване
на отрицателните
числа, т.е. ако S>N/2,
тя ще
представлява
кодова
комбинация
от втората
половина на
таблица 1.6.2.2.
Резултатът от
такова
събиране ще
има следния
вид:
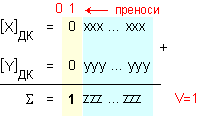
В
този случай
твърдението
на теоремата не
е вярно, т.е.
![]()
В същност,
n-битовата
сума
представлява
модула на
резултата,
т.е.
единицата в
знаковия разряд
е старшата
цифра на този
модул. Тази ситуация
представлява
положително
препълване
на диапазона
на
представимите
в цифровата
част на
разрядната
мрежа числа,
т.е.
препълване
подобно на (1.2.3).
Това препълване
се
разпознава
по факта, че
при събиране
на
положителни
числа е
получен резултат
с
отрицателен
знак, което е
абсурд. В случая,
кодова
комбинация
от втората
половина на
кодовата
таблица може
да бъде
получена
само в
резултат на
пренос в знаковия
разряд на
разрядната
мрежа
![]()
(вижте фигура
1.1.6.1.3).
Случай II.
Известно е,
че X<0 и Y<0.
Следователно X+Y<0.
В
този случай
![]()
Така в
разрядната
мрежа се
събират две
кодови
комбинации
от втората
половина на
кодовата
таблица 1.6.2.2.
Тогава е
абсолютно
сигурно, че
кодовата
сума S
излиза извън
изобразяващата
област, т.е. S>N и възниква
пренос от
най-старшия
разряд на
разрядната
мрежа, т.е.
![]()
Формално по
силата на (1.6.2.10)
кодовата
сума е числото
![]()
Поради
ограничената
дължина на
разрядната
мрежа, в нея
се запазват
само
младшите n
разряда на
тази сума.
Ситуацията
се характеризира
с
настъпилото
препълване
от вида (1.2.3). Разгледано
като число,
съдържанието
на разрядната
мрежа
представлява
разликата
![]()
която
е число,
сравнимо със
сумата S
по същия
модул.
Ако
резултатът N-|X+Y| попада в
зоната за
изобразяване
на отрицателните
числа, т.е. ако N-|X+Y| > N/2, , то
твърдението
на теоремата е
вярно.
Резултатът
от такова
събиране има
вида:
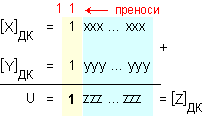
и можем да
запишем
![]()
Ако
резултатът N-|X+Y| попада в
зоната за
изобразяване
на положителните
числа, т.е. ако N-|X+Y| < N/2, то
твърдението
на теоремата не
е вярно, т.е.
![]()
Резултатът от такова събиране ще има вида:
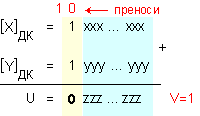
Тази
ситуация
представлява
отрицателно
препълване
на диапазона
на
представимите
числа. Това препълване
се разпознава
по факта, че
при събиране
на отрицателни
числа е
получен
резултат с
положителен
знак, което е
абсурд.
Аналогично
на предидущия
случай и сега
твърдим, че
получената в
знаковия
разряд нула в
същност е
старшата
цифра на
модула на
резултата. В
това можем
лесно да се
убедим, ако
изпълним
същата операция,
но в разрядна
мрежа с
по-голяма
дължина. В
случая,
кодова
комбинация
от първата половина
на кодовата
таблица може
да бъде получена
само в
резултат на
липсата на
пренос в
знаковия
разряд на
разрядната
мрежа
![]()
(вижте фигура
1.1.6.1.3).
Случай III.
Известно е,
че знаците на
операндите
са различни,
но X+Y>0.
В
така
определената
комбинация
от знаци се
събират една
кодова
комбинация
от първата
половина и
една кодова
комбинация
от втората половина
на кодовата
таблица 1.6.2.2,
като получената
кодова сума
следва да
бъде
комбинация
от първата
половина на
кодовата
таблица.
Събирането
на тези две
кодови
комбинации
се изразява
според (1.6.2.10)
така:
![]()
ако
приемем без
загуба на
общност, че
положителното
число е X, (X>0).
При
условията на
този случай,
разликата (X-|Y|) може да бъде
заменена със
сумата X+Y и тогава
кодовата
сума приема
вида S=N+(X+Y).
Очевидно
сумата S излиза
извън
областта за
изобразяване
на числата (S≥N),
което
означава, че
тя не е във
възможностите
на
разрядната
мрежа. В този
смисъл,
оставащата в
разрядната
мрежа младша
част на кодовата
сума,
представлява
разликата
![]()
която е
число,
сравнимо със
сумата S по същия
модул.
Отбелязахме,
че кодовата
сума S
е число
по-голямо от
модула на
разрядната мрежа
N, но в същото
време то не
може да
надхвърли
числото (N+N/2), т.е.
![]()
следователно
![]()
което
доказва, че
останалото в
разрядната мрежа
число U=X+Y се намира
в зоната за
изобразяване
на положителните
числа и на
него
съответства
кодова комбинация
от първата
половина на
кодовата
таблица 1.6.2.2.
Следователно
твърдението
на теоремата
в този случай
е вярно.
Резултатът
от такова
събиране има
вида:
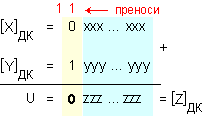
и
тогава можем
да запишем
![]()
Случай IV.
Известно е,
че знаците на
операндите
са различни,
но X+Y<0.
В
така
определената
комбинация
от знаци се
събират една
кодова
комбинация
от първата
половина и
една кодова
комбинация
от втората
половина на
кодовата таблица
1.6.2.2, но
получената
кодова сума
следва да бъде
комбинация
от втората
половина на
кодовата
таблица.
Събирането
на тези две
кодови
комбинации
се изразява
според (1.6.2.10)
така:
![]()
ако
приемем без
загуба на
общност, че
положителното
число е X, (X>0).
Тъй
като
предварително
е известен
знакът на
сумата от
числата, то
изразът (X-|Y|) може да бъде
заменен с
еквивалентният
му: -|X+Y|.
Тогава
кодовата
сума
представлява
числото
![]()
за която
очевидно е в
сила
ограничението
отгоре S<N,
което
означава, че
тя е във
възможностите
на
разрядната
мрежа.
Сумата е
ограничена и
отдолу, като
се има предвид,
че X+Y<0,
т.е. тя не може
да бъде
пo-малка от N/2.
Тогава
кодовата
сума е в
интервала
![]()
което
означава, че
тя попада в
зоната за изобразяване
на
отрицателните
числа и представлява
допълнителния
код на сумата
от числата.
Резултатът
от такова
събиране има
вида:
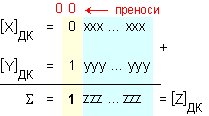
В
този случай
твърдението
на теоремата е
вярно и
можем да
запишем
![]()
И така, твърдението, че n-разрядната сума от допълнителните кодове на числата представлява допълнителния код на сумата от числата, е вярно във всички случаи, освен в случаите, когато се получава препълване на диапазона на представимите числа. Веднага трябва да се отбележи, че това препълване няма нищо общо с препълването на разрядната мрежа от вида (1.2.2), което беше използвано в процеса на доказване на теоремата.
Следствия:
Очевидно
неверният
резултат,
който се
получава в
описаните
случаи на
препълване,
трябва да се
отбелязва
чрез
признака за
препълване V.
Абсурдността
на резултата
при неговото
нормално
интерпретиране
има своята
логика и тя
беше
изяснена в
процеса на
доказване на
теоремата.
Ето защо
разпознаване
на
препълването
се постига с
помощта на
логическа
функция,
синтезирана
върху тази
логика.
Както
се вижда в
доказателството,
препълването
се изявява по
две
паралелни и
различни
линии. В
единия
случай беше
обръщано внимание
на абсурдното
съчетание на
знаците на
операндите и
знака на
резултата, а
в другия
случай препълването
се
обосноваваше
чрез възможните
преноси в и
от знаковия
разряд. Въз
основа на
тези
наблюдения
логиката на
препълване
на
разрядната
мрежа може да
бъде изразена
с две
различни, но еквивалентни
логически
функции:
·
Чрез
знаците:
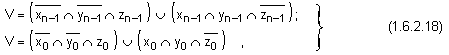
което
означава, че
препълване V=1
се открива,
ако знакът на
сумата не
съвпада със
знаците на
операндите.
Функцията е
представена
в два
варианта
според
номерацията
на разрядите
в РМ с ДФЗ и в
РМ с ЛФЗ.
Логическата
функция е
дизюнкция от
два елемента,
съответстващи
на
отрицателно
препълване
(случай I) и на
положително
препълване
(случай II). Стойностите
на тази
функция се
интерпретират
според
кодировката
(1.2.2).
·
Чрез преносите:
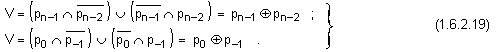
Според преносите в и от знаковия разряд, препълване се открива, ако те са различни. Останалото, казано по-горе, се отнася и за този вид на функцията.
Операция
събиране на
числа,
представени
в машинни
кодове е
изключително
важна и
нейната
апаратна
реализация е
изложена
най-подробно
в книга [2].
Там
читателят ще
намери
изобилие от
числени
примери,
илюстриращи
всички
по-горе изложени
особености.
Устройствата
и алгоритмите
за цялостно
реализиране
на тези изчисления
са изложени
тук в глава 3.
Следващият
раздел е:
1.6.3
Модифицирани
машинни
кодове ( Modified
machine codes )