1.6.3 Модифицирани машинни кодове

Modified machine codes

Откриване на препълването чрез (1.6.2.18) и (1.6.2.19) е откриване чрез косвени за резултата признаци – знаци, преноси. Съществуват причини, по силата на които, изведените по-горе зависимости не винаги могат да се приложат. Типичен пример е всяка операция от натрупващ тип. Операциите от наптрупващ вид се характеризират с това, че те се изпълняват винаги с резултата от предидущото действие. При тази постановка операция събиране Z=X+Y например ще се изпълни както следва

Z:=X ,

Z:=Z+Y .

Така след събирането първият операнд X не съществува, тъй като с тази организация е съобразена логическата структура на АЛУ, както и алгоритъма за функционирането му. Това означава че не съществува и неговия знак. Ето защо, интерес представлява възможността да се постигне откриване на препълване чрез самия код на резултата. Във връзка с това сега е моментът да припомним казаното в §1.2, че при препълване, сумата по същество се удължава с едни старши разряд, следователно при препълване се разрушава знакът. Знакът се унищожава, но в знаковия разряд се оказва старшата цифра на истинския резултат.

Така поставената задача отново търси решение в смисъла на понятието сравнимост по модул. За да се използва кода на резултата за разпознаване на препълване, което е два вида – положително и отрицателно, е необходимо в него да се въведе излишък. С помощта на този излишък следва да се търси възможност за изобразяване на резултати с описаните качества, но при запазени възможности на разрядната мрежа. Така излиза, че излишъкът се свързва с правата задача на сравнимостта, за която ще търсим неединствено решение.

Според така изложената идея, трябва да се избере такова съотношение между модула за сравнимост M и размера на областта за изобразяване L, че правата задача да има много решения. Последното се постига при съотношението L>(М-1). Излишеството или с други думи – удовлетворяване на посоченото неравенството, се постига много лесно чрез въвеждане на един допълнителен бит отляво на разрядната мрежа. Така дължината на кодовите комбинации става (n+1)[b], а модулът за сравнимост ще бъде

M = 2.N . (1.6.3.1)

При така определените параметри, разрядната мрежа, в която ще се представят модифицираните кодове на числата, ще има следния вид

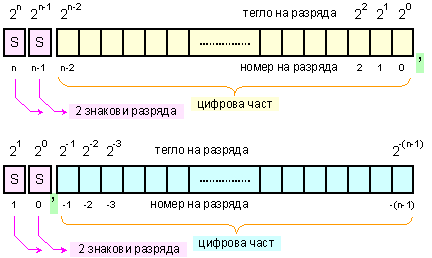
Фиг. 1.6.3.1. Структура на двоична разрядна мрежа за модифицирани кодове

Битовете за представяне на знака са два. Старшият допълнителен бит има свое отделно предназначение, което означава, че дължината на цифровата част на разрядната мрежа не се променя, т.е. диапазонът на представимите числа остава същия (вижте (1.6.2.13) и (1.6.2.14)). Дължината на изобразяващата област обаче, по силата на двоичната бройна система, се удвоява и става L=(2.N-1).d.

И така, ще повторим резултатите след въвеждане на допълнителния бит – диапазонът на представимите числа не се променя, а дължината на изобразяващата област се удвоява.

Ако преди изобразяващата област се разделяше на две части – за положителни и за отрицателни числа, то сега изобразяващата област може да се раздели на 4 части. Две от тези части продължават да изобразяват съответно положителните и отрицателните числа, а другите две допълнителни подобласти са за числата съответно с положително и отрицателно препълване. Казаното е представено нагледно с рисунката от фигура 1.6.3.2.

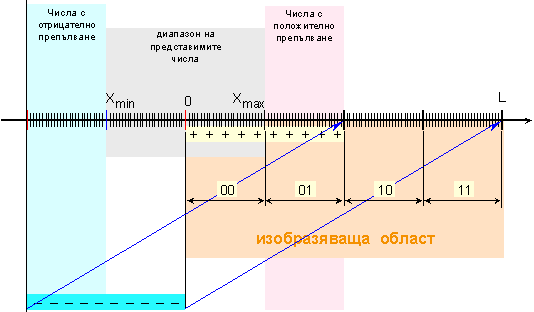
Фиг. 1.6.3.2. Схема за изобразяване с модифициран модул

Получените подобласти са:

1. Подобласт за изобразяване на представимите положителни числа –

Тя съвпада с първата четвърт на кодовата таблица, в която старшите два бита на двоичните комбинации имат стойностите 00.

2. Подобласт за изобразяване на числата с положително препълване –

Тя съвпада с втората четвърт на кодовата таблица, в която старшите два бита на двоичните комбинации имат стойностите 01.

3. Подобласт за изобразяване на числата с отрицателно препълване –

Тя се съпоставя на третата четвърт на кодовата таблица, в която старшите два бита на двоичните комбинации имат стойностите 10.

4. Подобласт за изобразяване на представимите отрицателни числа –

Тя се съпоставя на четвъртата четвърт от кодовата таблица, в която старшите два бита на двоичните комбинации имат стойностите 11.

Старшите два бита на кодовите комбинации са еднакви за първата и четвъртата подобласти, точно съответстват на знака на числата, попадащи в тези подобласти и следователно могат да се нарекат знакови. Очевидно е, че старшите два бита могат да се използват за разпознаване на подобластта за изобразяване на резултата. Може още да се забележи, че лявата цифра на знаковата двойка и в четирите подобласти е еквивалентна на истинския знак на резултата. От тук следва и крайният извод – ситуацията препълване на диапазона на представимите числа може да бъде разпозната по несъвпадението на стойностите в двата знакови бита на кодовата сума. Тогава логическата функция на признака за препълване е логическата функция нееквивалентност на старшите разряди:

където с z_n и с z_n-1 са означени оставащите в суматора старши разряди на кодовата сума. Така непосредствено върху получения резултат се постига разпознаване на препълването, както беше пожелано!

Синтезираният по този начин код се нарича модифициран допълнителен код и за него е в сила твърдението на теорема (1.6.2.17):

при условие, че няма препълване.

По същата логика (на допълнителния знаков разряд) може да се определи представянето на едно число в модифициран прав код.

Ще завършим с краткото пояснение, че логиката на операция изваждане на числа, представени в допълнителен или модифициран допълнителен код, е същата, каквато е в прав код – знакът на операцията се пренася върху знака на втория операнд и операция изваждане се заменя със събиране:

Тъй като вторият операнд сменя своя знак, то той преминава в друга подобласт за изобразяване, където се представя от друга кодова комбинация. Получаването на тази кодова комбинация от изходната е актуален въпрос, който предстои да бъде изяснен.

Следващият раздел е:

1.6.4 Преобразуване на машинните кодове ( Machine codes' conversion )