1.6.4
Преобразуване
на машинните
кодове
Machine codes
conversion
След
като в §
1.2 и в § 1.3 беше
изяснено, че
оперирането
с естествения
вид на
числата е
затруднено,
беше потърсено
удобно за тях
представяне.
Такова беше
намерено в
лицето на
допълнителния
код.
Удобството
на този код
се състои в това,
че
оперирайки в
негови
условия, се
освобождаваме
от
проблемите,
които
пораждат знаците
на числата. С
други думи,
при операция
събиране и
при операция
изваждане, в
крайна
сметка ние
винаги
събираме две
кодови
комбинации.
Свеждането
на тези
операции до
обикновено n-битово
събиране се
постига
благодарение
на теорема (1.6.2.17).
Тъй като
операция
събиране има
своята техническа
реализация,
то вече е
напълно ясно,
че
оперирането
с числата е принципно
решима
задача.
Това, което остава все още неизяснено е как ще се пренасяме от нашите естествени условия в условията на горе споменатата теорема и обратно. Следователно тук става въпрос за това как от естествения вид на числата ще получаваме техния допълнителен код и обратно, когато получим резултат, който е в допълнителен код, как ще го преобразуваме в неговия естествен вид. Въпросът е актуален, тъй като математическата формула (1.6.2.10), с която определихме кода, съдържа в себе си операция изваждане, от която всъщност искахме да се избавим. От този “омагьосан кръг” разбира се има изход и той ще бъде изяснен по-долу.
Преходите
от естествен
вид на
числото към код
и обратно
следва да се
постигат
чрез операции,
които имат
техническа
реализация, ето
защо чисто
математическото
определение
не е
достатъчно.
За да получим
необходимото
решение на
проблемите, свързани
с преходите,
следва да
включим в разглеждане
някои
допълнителни
обстоятелства.
Съществуват
две много
важни обстоятелства,
които в
подобни
ситуации ни
помагат. На първо
място трябва
да обърнем
внимание на факта,
че преди да
се пристъпи
към
определяне
кода на
дадено число,
то се
представя в двоична
бройна
система. От
математическа
гледна точка
този факт е
без значение,
но в смисъла на
тук
поставената
задача, той
има решаващо
значение,
защото той е
свързан с друг
един факт,
според който
двоичните
цифри могат
да се
интерпретират
като логически
константи. Тези
обстоятелства
са в основата
на техническата
реализация
на операция
събиране, което
е подробно
изложено в книга [2].
В
търсене на
алгоритъма
на прехода от
число към
код, ще
отбележим, че
като начало
следва да
бъдат
осигурени
изходните
предпоставки,
а именно –
числото да
бъде
изобразено в
двоична
бройна
система и да
бъде поместено
в разрядната
мрежа. С
други думи
процесът на
получаване
на
допълнителния
код ще
изхожда от
съдържанието
на
разрядната мрежа,
което според
споменатите
предпоставки
представлява
правия код
на числото
(вижте
определения
(1.6.1.1) и (1.6.1.2)).
По-нататък,
по силата на
(1.6.2.10), трябва да
се анализира
знакът на
числото, т.е.
съдържанието
на (n-1)-първия
бит на
разрядната
мрежа (вижте
фигура 1.1.6.1.3). Ако
числото е
положително,
съдържанието
на
разрядната
мрежа остава
непроменено,
но вече се
нарича
допълнителен
код, т.е.
![]()
Ако
обаче
числото е
отрицателно,
допълнителният
код
представлява
числото
![]()
Тъй като
модулът на
кода е равен
на модула на
разрядната
мрежа N (1.6.2.6),
записаната
разлика е
числото
![]()
Последният
вид на
разлика ще
интерпретираме
въз основа на
особения вид
на
умаляемото,
което може да
бъде изразено
така
N =
(N-d) + d , (1.6.4.1)
където d
е дискретът
на
разрядната
мрежа (1.1.6.1.4).
След
като
кодовата
комбинация
се интерпретира
като число без
знак с дясно
фиксирана
запетая,
тогава можем
да приемем,
че d=1 или N=(N-1)+1. Ще
означим
специално
полагането
![]()
Замествайки
получения
израз, за
допълнителния
код ще
получим
следния
израз:
![]()
Полученият
израз може да
се
интерпретира
като
съставен от
две части –
част първа:
![]()
и част втора: +1.
Както
се вижда,
операция
изваждане
продължава
да присъства в израза. Ако
успеем обаче
да намерим
стойността
първата част,
достатъчно е
към нея да
прибавим
единица и ще
получим
допълнителния
код.
Ясно
е, че
проблемът ни
е в първата
част на израза
(1.6.4.3).
Умаляемото
на тази
разлика е
числото
![]()
което
според
предварителните
констатации
може да бъде
записано
така:
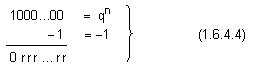
Както
може да се
види,
изпълнението
на операция
изваждане по
определение
води до резултат,
който
представлява
n-разрядно
число,
съдържащо
във всеки
отделен
разряд една и
съща цифра.
Тази цифра r,
определена в пункт 1.1.1, е максималната
за
съответната
бройна
система (r=q-1). В случай на
двоична
бройна
система r=1. При
това
положение
разликата
![]()
представлява
n-разрядно
число
съставено
само от
единици.
Сега
вече остава
да
разгледаме
двоичната разлика Q-|X|, която след
горните
съждения ще
запишем
както следва:
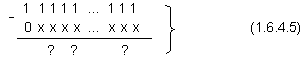
Модулът
на числото,
като
умалител в
горната
разлика, е
изразен със
старша
незначеща цифра
нула, тъй
като
позволената
дължина на цифровата
част на
разрядната
мрежа е (n-1) разряда (вижте
фигура 1.1.6.1.3).
В
така
представения
запис се
вижда, че
търсената
разлика може
да се получи
поразрядно,
т.е. всяка
нейна цифра
се получава
като разлика
от
максимално
възможната
за бройната
система и
текущата на
числото:
![]()
Тъй като
при това
положение възникването
на заеми е
невъзможно,
то
резултатът
във всеки
един разряд
ще се получи
независимо
от
резултатите
в останалите
разряди, т.е. поразрядно.
И
така, все още
не сме се
освободили
от операция
изваждане. За
сега успяхме
само да я
сведем от
многоразрядна
към едноразрядна.
Резултатът
от
едноразрядната
операция
изваждане
обаче може да
бъде изразен
както следва:
![]()
който лесно
може да бъде
доказан, ако
променливата
в дясната
част на
равенството
се интерпретира
като логическа!
По силата на
този извод се
стига до
заключението,
че
поразрядното
двоично
изваждане
може да бъде
заменено с поразрядна
логическа
операция
инверсия,
т.е.
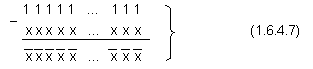
Този
резултат е
забележителен
с това, че той
се получава не
в резултат на
фактическо
изпълнение на
операция
изваждане, а
в резултат на
оползотворените
предпоставки,
на които
по-горе беше
обърнато
внимание.
Така
за
отрицателни
числа може да
се запишем,
че
![]()
което
изразява
аналитично
процеса на
преход от
прав код на
числото
![]()
в
допълнителен.
Въз
основа на
същия анализ
може да се
покаже, че
преходът от
допълнителен
код в прав код
може да се
извърши в
същия
порядък,
вместо в
обратен, т.е.
![]()
Зависимостта
(1.6.4.8) изразява
същността на
процеса на
решение на
правата
задача за
сравнимост,
изразен на
фигура 1.6.2.4. С
други думи
зависимостта
е циклическа:
![]()
Последното
означава, че
вместо два
алгоритъма
за преход от
един код в
друг, може да
се използва само
един – този
за преход от
прав в
допълнителен
код.
Всички
заключения,
направени в
този раздел,
са числено
илюстрирани
с множество
примери,
които
читателят
може да на
мери в книга
[2].
Следващият
раздел е:
1.6.5
Обратен код
( One's complement
representation )