1.6.6
Двоично-десетични
машинни
кодове
Binary decimal codes
По-рано
тук в § 1.1
и конкретно в
пункт 1.1.6.3 бяха
изложени
проблемите
отнасящи се
до
непосредственото
представяне
на числата в
десетична
бройна
система. Сега
е ред да поясним
правилата за опериране
с 2/10-чно
представените
числа. Ще направим
това тук и за
два от 2/10-чните
кодове, които
намират
приложение
на практика –
за кода на
прякото
заместване
(код 8421) и за
кода с излишък
три (код 8421(+3)).
Обект
на научен
интерес за
автора са били
още кодовете
(2421) и (5211), с които
читателят
може да се
запознае от
съответните
публикации:
http://www.tyanev.com/resources/docs/Document_V_46.pdf
http://tyanev.com/resources/docs/BCD_Adder_in_a_weight_code-5211.pdf
Ще
припомним
показаното в
раздел 1.1.6.3, че
броят на
4-битовите
2/10-чни кодове е
повече от 29
милиарда,
което ни
прави
песимисти
относно
надеждата, че
някой е
постигнал
изчерпателното
им изследване.
И
тъй като ще
стане дума за
числа със
знак, то
неминуемо ще
трябва да
развием
въпроса за
машинното
представяне
на 2/10-чните
числа със
знак.
А)
Операция
аритметическо
събиране в
код 8421
Разсъжденията,
които ще
бъдат
изложени във
връзка с
реализацията
на операция
събиране,
могат да
послужат
като основа
за анализ на
реализацията
й във всеки
друг код.
Кодовата
таблица на
десетичните
цифри в случая
е следната
Таблица
1.6.6.1
Кодово
съответствие
|
цифра |
8 4 2 1 |
|
0 |
0 0
0 0 |
|
1 |
0 0
0 1 |
|
2 |
0 0
1 0 |
|
3 |
0 0
1 1 |
|
4 |
0 1
0 0 |
|
5 |
0 1
0 1 |
|
6 |
0 1
1 0 |
|
7 |
0 1
1 1 |
|
8 |
1 0
0 0 |
|
9 |
1 0
0 1 |
Тъй като кодът на десетичните цифри няма отношение към правилата на бройната система, в която се представя дадено число като стойност, то операция събиране на двоично-десетични числа се провежда според зависимостта (1.2.1), в която цифрите, сумата и преносите имат десетична интерпретация.
В
поразрядното
събиране
![]()
вземат
участие
десетичните
цифри xi и
yi, които са
кодирани и
представени
с 4-разрядните
двоични
комбинации
на кода на
прякото
заместване
(според
таблица 1.6.6.1) и
десетичният
пренос от
по-младшия
разряд pi-1. Тъй като
елементите
на тази сума
са двоично
представени,
това
събиране може
да бъде
изпълнено по
правилата на
двоичната
бройна
система в
един
4-разряден
двоичен
суматор.
От
всичките
възможни
двоични суми S обаче има
такива, които
не са
елементарни
количества
според
десетичната
бройна система,
т.е. не всяка
сума
съответства
на десетична
цифра. Според
свойствата
на кода само
сумите, които
не
предизвикват
десетичен
пренос, имат
правилно
съответствие.
Всяка
поразрядна
сума S,
която
съответства
на
количества
от 0 до 9 може да
се приеме за
вярна и
окончателно
готова.
За
съжаление
могат да се
получат суми,
които
нахвърлят
числото 9.
Такива са
всички числа
от 10 до 19. Според
правилата на
десетичната
бройна
система тези
числа не са
елементарни
количества и
за тяхното
означаване
няма символи
(цифри). Така
според (1.2.1),
тези суми
предизвикват
десетичен
пренос. Някои
от сумите
обаче (10, 11, 12, 13, 14 и 15)
се оказват
във
възможностите
на 4-битовия
двоичен суматор
и не
предизвикват
необходимия
десетичен
пренос, при
това
получената
двоична сума
не
съответства
на нито една
кодова
комбинация. Например 5+5=10
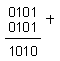
Тази
ситуация
представлява
проблем, тъй
като
получената
сума не е
вярна (в
смисъла на
кода). Изход
от това
положение е
възможен отново
на
базата на
теорията за
сравнимост.
Желаният
резултат и
съответствие
(в смисъла на
кода) се
постигат
чрез
коригиране
на получената
сума чрез
допълнително
прибавяне на
6 единици.
Тази
константа (+6)
се определя
като
най-малкото
число, което
може да предизвика
необходимия
пренос. Корекцията
предизвиква
двоичен
пренос (p3=1)
с двоично
тегло равно
на модула на
4-те двоични
разряда (M=16), т.е.
![]()
в
резултат на
което в
текущия 2/10-чен
разряд
ще остане
числото
![]()
В
случая,
модулът на
кода M е по-голям
от размера на
изобразяващата
област L=q=10,
поради което
в този вид 6 от
комбинациите
на кода се
явяват
излишни. Така
че, корекцията
и
последващият
я тетраден
пренос,
могат да се
разбират
като
действия за
привеждане
на сумата в
изобразяващата
област [0, 9].
Съществуват още суми (16, 17, 18 и 19), които изискват разпространение на десетичен пренос според (1.2.1). Те обаче не са във възможностите на 4-битовата двоична сума (S>15) и предизвикват тетраден пренос, който ощетява оставащата в полето на суматора част от сумата с 16 единици, т.е. с 6 повече от желаните 10. Например 8+9=17
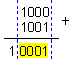
Естествено, така оставащата разлика не е правилна – не й достигат отнесените в повече 6 единици. Ето защо тя следва да бъде коригирана чрез възстановяване на отнетото й, т.е. чрез прибавяне на 6. Така в текущия 2/10-чен разряд се получава числото
![]()
Пълния
логически
синтез на
двоично-десетичния
суматор в код
8421, както и
множество
числени
примери,
читателят
може да
намери в книга
[2].
Б)
Операция
аритметическо
събиране в
код с излишък
+3
Отново според (1.2.1) разглеждаме само едноразрядно събиране на две десетични числа, чиито десетични цифри xi и yi са имитирани (представени) от 4-битови двоични комбинации
![]()
Кодовата
таблица на
десетичните
цифри в случая
е следната
Таблица
1.6.6.2
Кодово
съответствие
|
цифра |
(8421)+3 |
|
0 |
0 0
1 1 |
|
1 |
0 1
0 0 |
|
2 |
0 1
0 1 |
|
3 |
0 1
1 0 |
|
4 |
0 1
1 1 |
|
5 |
1 0
0 0 |
|
6 |
1 0
0 1 |
|
7 |
1 0
1 0 |
|
8 |
1 0
1 1 |
|
9 |
1 1
0 0 |
И в
този случай
поразрядното
десетично събиране
води до
двоично
събиране на
две 4-битови
кодови
комбинации,
представляващи
десетичните
цифри и
стойността
на преноса от
по-младшия
десетичен
разряд. Това
поразрядното
събиране
може да се
представи
така
![]()
където
сумите
![]()
изразяват
стойността
на
съответната
тетрада,
според
таблицата 1.6.6.2.
Очевидно
сумата (1.6.6.3) е
принципно
невярна (в
смисъла на
кода с
излишък +3), тъй
като тя винаги
съдържа три
единици в
повече. Така
всяка
първоначална
двоична сума
следва да
бъде
поправяна.
Поправката
обаче следва
да бъде
съобразена с
тетрадното
препълване,
ето защо
анализът на
възможните
кодови суми
изявява два
случая, които
разглеждаме
по-долу.
Ако при първоначалното събиране не се получи тетраден пренос (p3=0), кодовата сума S като двоична сума е вярна. Но тя е невярна в смисъла на кода и следва да бъде намалена с три единици. Така в текущия 2/10-чен разряд след включване на корекцията се получава числото
![]()
което,
както не е
трудно да се
види ще получи
съответствие
според
кодовата
таблица.
Ако
обаче при
първоначалното
събиране възникне
тетраден
пренос (p3=1), той
отнася от
тетрадната
сума 16
единици, представляващи
неговото
двоично
тегло
![]()
Тези 16
единици
можем да
интерпретираме
разложени в
следната
сума: 16=10+3+3.
·
Първите
10 единици
можем да
приемем за
съответстващи
на
необходимия
десетичен
пренос, тъй
като само
когато
десетичната
сума
![]()
в този код се
получава тетраден
пренос.
·
Следващите
три единици,
отнесени от
тетрадния
пренос, са
желани, тъй
като те
компенсират
принципната
грешка в
сумата.
·
Отнасянето
на
последните
три единици
обаче е
нежелателно,
тъй като с
това се
ощететява
кодовата
сума.
Следователно
се налага
тяхното
компенсиране.
Така
в текущия
2/10-чен разряд
след
включване на
корекцията
се получава
числото
![]()
За
разлика от
двоично-десетичната
корекция,
необходима
при събиране
в код 8421, в код с
излишък +3,
коригиращите
константи са
различни, при
това едната е
отрицателна
(-3). Неудобството,
което
последната
създава, се
отстранява
чрез
представянето
й в допълнителен
код, т.е.
корекцията (-3)
се заменя с 13,
според (1.6.2.10) или (13-М=13-16=-3).
Пълния
логически
синтез на
двоично-десетичния
суматор в код
(8421)+3, както и
множество
числени
примери,
читателят
може да намери
в книга [2].
В)
Машинни
кодове на
2/10-ните числа
със знак
Вече
многократно
беше заявено,
че същността
на машинните
кодове се
състои в
това, че те
способстват
за удобна
техническа
реализация
на основната
операция
(операция
събиране)
върху числа със
знак. Ето
защо
въпросът за
представяне на
2/10-ните числа в
машинен код е
актуален.
Естественият вид на тези числа води да техния прав код, т.е. до запълване на разрядната мрежа със знака и модула им. При необходимост в непопълнените позиции (разряди) се поставят незначещи цифри. Всичко казано до момента за правия код в общия случай се отнася и до 2/10-ните числа. Нещо повече, това се отнася и за останалите кодове. Ето защо, синтезът на тези кодове може да се счита по принцип за вече изложен.
Така
например, ако
се приеме, че
дължината на
една
десетична
разрядна
мрежа е n
разряда, то
нейният
модул N ще бъде
числото
![]()
Модулът
е число с
една единица
и n нули: 100...0. Тогава,
според
определението
(1.6.5.1) за обратен
код на едно
отрицателно
число, същият
ще се получи
в резултат на
следното
изваждане:
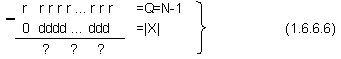
където dddd...ddd са
десетичните
цифри на
абсолютната
стойност на
числото X, а r е
най-голямата
десетична
цифра, т.е. r=q-1=9.
Според
тази разлика
излиза, че
обратният код
ще съдържа в
качеството
си на знак
минус
максималната
цифра r, т.е.
знакът е
кодиран с
двете крайни
десетични
цифри, които
в разрядната
мрежа са представени
от
съответните
4-битови
кодови
комбинации:
![]()
Цифровата
част на
обратния код
ще съдържа (n-1)
цифри, които
като цяло ще
представляват
число, което
допълва
абсолютната
стойност на
числото X,
до модула на
кода – Q. В този
смисъл, по изложени
в пункт 1.6.4
причини,
намирането
на обратния
код се свежда
до
поразрядното
изваждане
![]()
Тъй като
значещите
цифри в
десетична
бройна
система са
повече от
една,
фактическата
операция
изваждане (r-di) не може да
бъде
заменена
така лесно с
друга
операция
(удобна за
реализиране),
както беше в
двоична
бройна
система.
И
точно тук
следва да се
обърне
внимание на кода,
в който е
представена
десетичната
цифра di. Ако
използваният
код
притежава
свойството допълняемост,
то разликата (r-di) може да бъде
заменена с
тетрадната
инверсия на di, т.е.
обратният
код ще бъде
цифровата
последователност
![]()
където,
ако всяка
десетична
цифра е
представена
от своята
тетрада
![]()
то
![]()
Когато
като модул на
изобразяващия
код се приеме
модулът на
разрядната
мрежа N,
според (1.6.5.3) се
получава аналогът
на
допълнителния
код на
отрицателното
2/10-чно число X:
![]()
При
това всички
свойства на
тези кодове,
изложени в
пункт 1.6.4, са в
сила и за
техните
двоично-десетични
аналози.
Разгледаният
в точка Б) код
с излишък +3 за
кодиране на
десетичните
цифри притежава
свойството
допълняемост,
ето защо той
е твърде
ценен при
реализация
на
алгоритмите
за изваждане
и деление на
двоично-десетични
числа, т.е. за
двоично-десетичната
аритметика.
Другият
код – 8421, който
беше
разгледан в
точка А), не
притежава
свойството
допълняемост.
По тази
причина
построяването
за него на инверсни
кодове е
значително
по-трудоемко,
с всички
произтичащи
от това
усложнения
относно
реализацията
на
алгоритмите
за изваждане
и деление.
Налага се на
този код да
се спрем
специално.
Ако
изходим от
определението
(1.6.6.6), следва, че обратният
код на
отрицателни
числа, кодирани
в код 8421,
се получава
поразрядно
от разликите
![]()
Тъй
като
десетичната
цифра di е
представена
в кода на
прякото
заместване 8421,
то тя може да
се
интерпретира
като двоично
число с дясно
фиксирана
запетая.
Тогава обратният
код на една
десетична
цифра в отрицателно
число може да
се търси като
допълнение
до модула на
4-битовата тетрада
![]()
Но, тъй
като
двоичният
модул
![]()
на
тетрадата, е
с 6 единици
по-голям от
десетичния
модул на
разряда
![]()
то тази разлика трябва да се коригира в кода на десетичната цифра.
Тогава
окончателно
получаваме,
че
![]()
Последният
израз е
съставен с
цел да се покаже,
че взетото
решение е
еквивалентно
на определението.
Разликата
![]()
може да бъде
заменена с
логическа инверсия
на
тетрадната
сума (di+6) по
силата на
правилата за
изваждане на
двоично
число от
числото
![]() .
.
И
така,
обратният
код на
отрицателни
двоично-десетични
числа,
кодирани в
кода 8421,
се получава
след
поразрядно
събиране с цифрата
6:
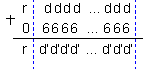
по правилата на двоичната бройна система (с разпространение на тетрадните преноси), след което се извършва поразрядна логическа инверсия във всяка тетрада според (1.6.6.8) :
![]()
Допълнителният
код се
получава от
обратния по
описания
вече начин:
![]()
С цел да се намали реалната двоична дължина на машинните кодове на двоично-десетичните числа, знаковият разряд може да се интерпретира и обработва като двоичен. Същото се отнася и за съставяне на модифицирани кодове. Това обаче не се отнася за разрядите, съдържащи незначещи цифри. Ако по някакви причини се налага знакът да съвпада със следващите го отдясно в разрядната мрежа незначещи цифри (по аналогия с двоичните числа), тогава знакът остава кодиран с десетична цифра.
На
читателят
оставяме
задачата да
докаже валидността
на
логическите
функции за откриване
на
препълване
при работа с
двоично-десетични
числа.
Mножество
числени
примери, отнасящи
се до
машинните
кодове на
2/10-чните числа,
читателят
може да намери
в книга [2].
Следващият
раздел е:
ГЛАВА 2 Представяне
на
логическите
структури ( Presentation of logical
structures )