Г Л А В А 2
ПРЕДСТАВЯНЕ НА
ЛОГИЧЕСКИТЕ
СТРУКТУРИ
PRESENTATION OF LOGICAL
STRUCTURES
§ 2.1
Изчислителен
процес
Calculation
process
Понятието
изчислителен
процес е
фундаментално
и за него
следва да се
постигне
правилното
разбиране.
Нашето разбиране
е, че
изчислителен
процес в
природата протича
единствено в
централния
мозък на висшите
живи
същества. С
други думи,
този процес
протича в
нашия мозък,
в резултат на
което ние
съществуваме
разумно или
още
съзнателно.
Разумно
означава
логично. В
този процес
на първо
място
участва
постъпващата
през
човешките
сензори
(осезателни
органи)
информация
за
заобикалящата
ни природа и
за всичко
случващо се
около нас.
Човешките
осезателни
органи
възприемат,
оценяват и
предават
чрез
нервната
система
информацията
до главния
мозък, където
тя се
преработва.
Главният
мозък е
втория и
най-важен
елемент в реализацията
на
изчислителния
процес. В резултат
на неговото
функциониране
се изработват
правилни
решения, т.е.
формира се
нова
информация.
Тази нова
информация е
третия елемент
в
изчислителния
процес. След
вземане на
решенията
главният
мозък ги
изпраща
отново чрез
нервната
система до
съответните
изпълнителни
органи. В
крайна
сметка, в
резултат на
този
непрекъснат
процес, ние съществуваме
съзнателно
във всеки
един момент. Вероятно
всеки
разбира, че
грешките,
които е
възможно да
допуснем (не
видял, не
осъзнал, не
преценил, не
чул, не
помирисъл, не
си спомнил,
не почуствал,
и прочие и пр.)
ще ни доведат
до неприятни
за нас крайни
резултати.
Върху всичко
това ние се
замисляме само
когато
искаме да
постъпим
правилно или
когато
искаме да
прехвърлим
нашите действия
върху друг
изпълнител.
Под друг изпълнител
читателят
вероятно
вече разбира,
че имаме
предвид
технически
реализиран.
Така
естествено
достигаме до
идеята за
машината, тази,
която ще
прави нещата
вместо нас и
която следва
да опознаем.
Не можем да
отделим тук повече
внимание за
анализ на
изчислитения
процес. Ще
отбележим
само, че
задълбоченият
му анализ
води до
разбирането,
че той е структурен
процес. В
него
съществуват
ясно
различими
елементи и
ясно
различими
връзки между
тях. Така
представата
ни за изчислителния
процес се
оформя като
разбиране за
определена
последователност
от действия,
които често
се налага да
обесняваме, с
които се
оправдаваме,
или
предаваме на
други.
Преди да представим каквото и да било конкретно техническо решение следва да изясним как ще направим това, т.е. с какви средства и по какъв начин ще представяме логическите структури и тяхното функциониране. Ето защо в тази глава ще бъдат изложени общите разбирания, правила и средства, които ще се използуват по-нататък за това.
Известно
е, че
процесът на
разрешаване
на всеки
проблем
започва с
етапа на
неговото осмисляне.
Обикновено
този етап е
свързан с различните
методи за анализ
на
възникналия
проблем (поставената
задача или
идея).
Получените
резултати и
направените
изводи са
основа за следващия
етап, който
се нарича синтез.
В сферата на
компютърната
техника и
компютърните
приложения
резултатът
от синтеза е
обикновено
някаква
схема за
действие, която
най-често се
нарича алгоритъм.
С други думи,
алгоритъмът
представя
анализирания
изчислителен
процес.
Реализацията
на създадения
алгоритъм е
всъщност
инженерното
решение на
възникналия
проблем.
Понятието
алгоритъм е
фундаментално
и тъй като
резултатите,
които ще представяме
по-нататък са
в най-пряка
връзка с
него, ще си
позволим да
го определим
строго.
Алгоритъм ще наричаме всяка последователностна схема от действия, която представя (описва) реален изчислителен процес и притежава следните свойства:
а) детерминираност ;
б) масовост ;
в) резултативност.
Изчислителната
схема е детерминирана,
когато
тръгвайки от
нейното
начало, всяка
възможна
пътека в
схемата
стига до
нейния край.
С други думи
всички
пътища от
началото
стигат до
край и в нито
една точка на
схемата няма неяснота
за
по-нататъшния
ход на
изчислителния
процес.
Естествено
всяка схема
има едно
начало и един
край.
Свойството
масовост е
свързано с
възможността
изчислителната
схема да се
прилага за
всяка
конкретна задача
от дадения
клас. С други
думи
изчислителната
схема
притежава
свойството общност,
присъщо на
математическите
изразни средства.
Осъзнавайки
силата на
това
свойство Готфрид
В. Лайбниц (1646-1716) е
написал
следното:
.....
“Необходимо
е да сведем
понятията до
символи,
символите до
числа и
най-накрая
чрез цифрите
и символите
да подложим
понятията на
механични
изчисления. .....
Тогава при
възникване
на спорни
въпроси
между двама
философа
няма да има
необходимост
от научна
дискусия.
Достатъчно
ще бъде те да
седнат зад
изчислителното
устройство и
да си кажат
(желателно
приятелски):
нека да пресметнем!”.
Свойството
резултативност
е свързано с
пълната
гарантираност
и разбираемост
на
получавания
резултат. При
всеки проход
от начало до
край алгоритмичната
схема гарантира
получаването
на резултат
(очакван и
разбираем).
Изчислителният
процес,
разбиран
като протичащ
във времето
процес, в
резултат на
който при
преработка
на
информацията,
в даден момент
се получава
очакваният
резултат, е структурен
процес.
Структурните
елементи на
този процес
са отделните операции,
изпълнявани
върху
данните.
Връзките
между
структурните
елементи са
детерминирани
и
еднопосочно
насочени във
времето. Наричат
се алгоритмични
преходи.
Едно от
най-използваните
средства за
представяне
на изчислителния
процес (на
алгоритъма)
са блок-схемите.
Употребяваните
основно
блокове са изобразени
на
следващата
фигура.

Фиг. 2.1.1.
Изразни
средства на
блок-схемите
Показани
са блок “начало”,
блок “край”, “операционен”
блок, “условен
алгоритмичен
преход”.
Стрелката,
поставена
най-отдясно,
обикновено
свързва
изхода на
един блок с
входа на друг
блок и следва
да се разбира
като означение
за “безусловен
алгоритмичен
преход”.
Ще
припомним основните
алгоритмични
структури и
техния вид.
Най-простата
алгоритмична
структура е линейната.
Нейният вид е
показан на
фигура 2.1.2-А). Тя
представлява
фиксирана
последователност
от операционни
блокове,
свързани с
безусловни
алгоритмични
преходи.
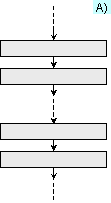
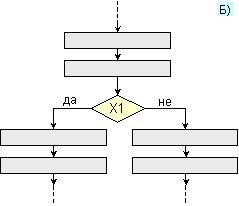
Фиг. 2.1.2. Линейна
и разклонена
алгоритмична
структура
С
помощта на
блок за
условен
алгоритмичен
преход се
изразяват разклонени
алгоритмични
структури –
фигура 2.1.2-Б).
Разклонената
алгоритмична
структура
съдържа и двете
възможности
за хода на
изчислителния
процес, които
са в зависимост
от
логическото
условие Х1.
Реалното
изпълнение
на
алгоритъма
обаче е свързано
с онзи клон,
който се
определя
чрез конкретната
логическа
стойност на
условието Х1.
Неизбраният
клон в този
момент
остава нереализиран,
но той
присъства в
схемата. В
това се състои
свойството общност
на тази
алгоритмична
структура.
По-сложните алгоритмични структури са свързани с така наречените повторения. Повторенията на изявена (обособена) група операции обикновено се откриват в процеса на анализ на изчислителния процес. Съставът на действията в групата зависи още от решението за представяне на алгоритмичната схема. Повторенията в хода на изчислителния процес са два вида:
·
Регулярни;
·
Нерегулярни.
Регулярни
са онези
повторения,
които се
повтарят
периодично,
без вмъкване
между тях на
други
действия. В
алгоритмичните
схеми тези
повторения
могат да
бъдат изразени
по два
начина:
·
Да бъдат
записани по
хода на
изчислителния
процес във
вид на
линейна
алгоритмична
структура
толкова пъти,
колкото пъти
се повтарят.
Този вариант
рядко се
използва на
практика,
защото той е
абсолютно
конкретен и
не притежава
свойството
общност.
·
Да бъдат
записани
само веднъж,
а повторението
им бъде
организирано
с
допълнителни
средства. В
този вариант
изразяването
на
регулярните
повторения
трябва да бъде
постигнато за
общия случай,
т.е. въз
основа на общи
формули,
описващи
повтарящото
се поведение
на съответните
величини.
Самото
повторение
се организира
с условен
алгоритмичен
преход, при
който се
проверява условието
за край на
повторенията.
Така се
получава
нова алгоритмична
структура,
различна от
разклонената,
която се
нарича циклична.
Видът на тази
структура е
показан на
фигура 2.1.3.
Както
може да се
види, тази
структура
има три
елемента: БПЦ
– блок за
подготовка
на цикъла; ТЦ
– тяло на
цикъла и УКЦ
– условие за
край на
цикъла. Ако
условието за
край на
цикъла не е
изпълнено,
алгоритмичният
преход се
връща назад,
към вече
изпълнени
действия С
този
алгоритмичен
преход назад
се
обезпечава
повторението
на действията,
включени в
тялото на
цикъла.
Точката, в която
се връща
преходът по
клона “лъжа”
се нарича входна
точка на
цикъла. В
текстовите
алгоритми
входната
точка се отбелязва
с етикет.
Преходът по
клона “истина”
се нарича нормален
изход от
цикъла. В
тялото на цикъла
могат да се
съдържат
условия,
според които
са възможни преждевременни
излизания
от процеса на
повтаряне.
Според
условието за
край на
циклите се
делят на два
вида:
·
цикли с предварително
известен
брой
повторения;
·
цикли с предварително
неизвестен
брой повторения.
Според
реда на
блоковете ТЦ
и УКЦ
циклите се
определят
като:
·
Цикли с послеусловие.
При тези
цикли (вижте
фигура 2.1.3)
действията от
тялото се
изпълняват задължително
поне един път.
·
Цикли с предусловие.
При тези
цикли
проверката
на условието
за край на
цикъла
предхожда
действията
от тялото, т.е.
входната
точка на
цикъла е
входа на условния
блок. Така
може да се
осигури изход
от цикъла без
нито едно
изпълнение на
действията
от тялото.
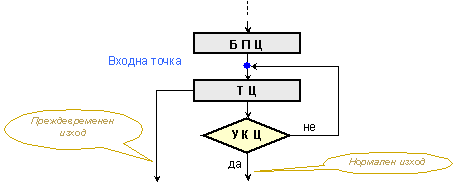
Фиг. 2.1.3.
Алгоритмична
структура
цикъл
Нерегулярните
повторения
се
характеризират
с това, че между
техните
повторения
могат да се
изпълняват и
други
действия. С
други думи, в
общия ход на
изчислителния
процес
нерегулярните
повторения
са повторения
от време на
време или
още
повторение на
едно и също
нещо, но само
когато има
необходимост
от него. Тази
именно
необходимост
е
нерегулярна.
Нерегулярното
повторение,
както и определянето
на състава на
операциите в
групата, обикновено
се откриват в
процеса на
анализ на
изчислителния
процес. Съставът
на
действията в
групата
зависи още от
решението за
представяне
на
алгоритмичната
схема.
И тези повторения, аналогично на регулярните, в алгоритмичните схеми могат да бъдат изразени по два начина:
·
Да бъдат
записани по
хода на
изчислителния
процес като в
една линейна
алгоритмична
структура толкова
пъти, колкото
пъти се
повтарят.
Този вариант
рядко се
използва на
практика, защото
той е
абсолютно
конкретен и
не притежава
свойството
общност.
·
Да бъдат
записани
само веднъж,
а повторението
им бъде
организирано
с
допълнителни
средства. За
разлика от регулярните
повторения,
нерегулярните
повторения не
могат да
бъдат
организирани
с показаните
на фигурите 2.1.1,
2.1.2 и 2.1.3
алгоритмични
преходи. За
да се изясни
същността на
тази
организация
показваме
нейния графичен
вид – фигура 2.1.4.
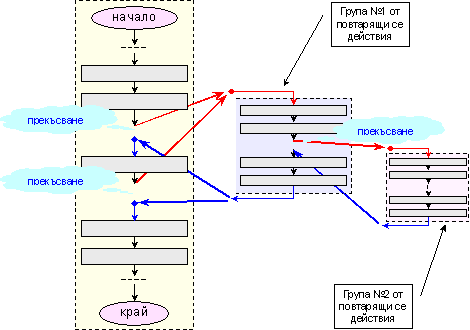
Фиг. 2.1.4.
Алгоритмичен
израз на
нерегулярни
повторения
На
рисунката е
изразен един
основен
алгоритъм с
показани
начало и
край. На две
места по хода
на неговото
изпълнение
са изявени повтарящи
се действия, които
са изнесени и
записани
отделно и само
веднъж
(група №1).
Показано е,
че този
подход може
да бъде
приложен и
върху друга
така
изнесената
група
действия – в
нея също са
възможни нерегулярни
повторения
(група №2).
Рисунката изразява
функционирането
на
изнесените
групи, чиито
действия се
повтарят
винаги,
когато в
текущо
функциониращия
алгоритъм
има
необходимост
от тях. При
това
изпълнението
на текущия
алгоритъм се
преустановява
(прекъсва)
временно.
Стоящи
вън и
независимо
от една от
друга както и
от основния
алгоритъм,
тези групи
действия, при
това
повтарящи се,
явно следва
да притежават
свойството общност.
С други думи,
те следва да
се
изпълняват
всеки път,
когато към
тях се
осъществи
обръщение, но
върху
различни и
конкретни
данни. При
тяхното първоначално
съставяне
обаче
отчитането на
тази
конкретност
е невъзможно,
ето защо на
тях следва да
се гледа като
на самостоятелни
алгоритмични
схеми в
пълния
смисъл на
даденото за
това понятие
определение,
съставяни за
общия случай.
Тъй като тези
алгоритми са
предназначени
да обслужват
други алгоритми,
които ще се
обръщат към
тях, програмната
им
реализация
носи
наименованието
подпрограма,
което
изразява
подчинеността
им. Подпрограмите
се
възприемат
като специализирани
програмни
инструменти.
Всеки път, когато в текущо изпълнявания алгоритъм възникне необходимост от групата действия на една подпрограма, тяхното подключване към общия ход на изчислителния процес се осъществява с безусловни алгоритмични преходи. Тези алгоритмични преходи обаче са особени и те трябва да решават две задачи:
·
Да
реализират
безусловен
алгоритмичен
преход към
подпрограмата,
като при това
осигурят
възможността
за връщане
към
алгоритъма,
който ги е
повикал.
Когато извиканата
за
изпълнение
подпрограма
завърши, тя
от своя
страна
трябва да изпълни
обратен
безусловен
алгоритмичен
преход, с
който да се
възстанови
хода на преди
това
прекъснатия
алгоритъм.
·
При
всяко
обръщение
към
подпрограмата
нейното
изпълнение
следва да се
реализира върху
конкретните
за случая
данни.
Естествено, в
резултат се получават
и конкретни
данни, които
са необходими
на
алгоритъма,
извършил
обръщението
към
подпрограмата.
Ето защо
всяко обръщение
към
последната е
свързано със
задачата за
организация
на предаването
на
конкретните
данни.
Конкретните
данни за
всяко
изпълнение
се наричат действителни.
Действителните
данни се
присвояват
като стойности
на формалните
променливи, с
които е
запрограмиран
алгоритъма
на
подпрограмата.
За
по-лесно
изобразяване
на
нерегулярните
повторения
се определя
специална
форма на
операционен
блок, който е
представен
на фигура 2.1.5.
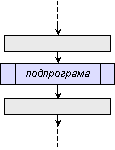
Фиг. 2.1.5.
Изразяване
на действия,
отделени в самостоятелен
алгоритъм
(подпрограма)
Така
представените
задачи на
алгоритмичните
преходи за
работа с
подпрограми
имат своята
техническа реализация,
която ще бъде
изяснена
по-нататък в
тази книга (глава 5).
Реализацията
на всеки
създаден
алгоритъм
може да бъде
осъществена
по различни
начини, в
зависимост
от
първоначално
наложените
ограничения,
изисквания и
критерии. Две
са основните
възможности:
програмна
реализация
върху универсални
изчислителни
средства или
апаратна
реализация
чрез
специализирани
технически
средства. Не
изключваме и
смесен вариант.
Тук, в тази книга, поради спецификата на разглежданите алгоритми, ще става дума най-вече за подходите към тяхната апаратна реализация. Това се обосновава преди всичко от самото средство, което е предмет на съдържанието – цифровата изчислителна машина. Тъй като тази машина е едно техническо решение на реални потребности, тук ще бъдат илюстрирани средствата за неговото ясно и разбираемо представяне, т.е. за изясняване на неговото съдържание и функциониране, при определена степен на детайлизация.
Следващият
раздел е:
§ 2.2
Същност на
структурния
подход ( Essence of the structural approach )