3.2.1
Операция
събиране,
операция
изваждане
Addition and subtraction
Вече беше казано много за тези операции. В най-общия случай операция събиране се изпълнява върху числа със знак и следователно събирането е алгебрическо, т.е. с приложение на инверсни кодове – обратен или допълнителен. Това означава, че операндите ще встъпват в тази операция вече изобразени в инверсен (машинен) код. Тъй като принципна разлика между обратен и допълнителен код няма, за числата с фиксирана запетая тук ще бъде приет за подразбиращ се допълнителен код. Този избор позволява различна интерпретация на съдържанието на разрядната мрежа – като число със знак или като число без знак и в голяма степен облекчава паралелно-последователната обработка.
Алгоритъмът
за
изпълнение
на операциите
събиране и
изваждане е
тривиален и
по същество
той е изразен
със
зависимостите
(1.6.2.17), (1.6.3.3) и (1.6.3.4).
Самото
събиране се
извършва според
системата
уравнения (1.2.1),
която намира
своята
реализация в
лицето на
суматора. С други
думи, за да се
построи
устройство
за събиране,
на първо
място е
необходим
логически
възел, наречен
суматор.
Необходимо е
да се
разгледат обаче
и двата вида – комбинационен
и натрупващ.
Ако изборът е
комбинационен
суматор, това
означава, че
на неговите
два входа операндите
следва да се
подават в
едно и също време.
Като се има
предвид, че
операндите
идват в
устройството
за събиране
от едно и също
място
(оперативната
памет) – последователно
един след
друг, това
означава, че
входовете на
суматора
следва да бъдат
свързани с
възли за
временно
съхранение
на операндите.
Такива възли
могат да
бъдат два
входни
регистъра. Синтезът
на суматора
като
логически
възел, в
най-разнообразни
варианти,
читателят ще
намери в книга
[2].
Тъй като
изходът на
комбинационния
суматор
поддържа във
времето
резултата
само докато
на входа се
подават
събираемите,
то се налага
включването
на регистър
за запомняне
на резултата.
Като се вземат под внимание предпоставките, изложени по-горе, както и свеждането на операция изваждане към операция събиране (след смяна на знака на втория операнд), се формира окончателно логическата структура на устройството, показана на фигура 3.2.1.1.
Логическата структура съдържа следните логически възли:
·
РгХ –
Регистър за
първия
операнд (n-битов,
изграден от
асинхронни
RS-тригери с
право
управление,
структура Latch,
записващ
данни
еднофазно с
предварително
нулиране –
вижте
съответния
раздел в книга
[2]).
·
РгY – Регистър
за втория
операнд
(n-битов,
изграден от
асинхронни
RS-тригери с
право
управление,
структура Latch,
записващ
данни
еднофазно с
предварително
нулиране).
·
БуфРг – Буферен
(помощен)
регистър
(n-битов,
изграден от
асинхронни
RS-тригери с
право
управление,
структура Latch,
записващ
данни
еднофазно с
предварително
нулиране).
·
РгСМ – Регистър
за сумата
(n-битов,
изграден от
асинхронни
RS-тригери с
право
управление,
структура Latch,
записващ
данни
еднофазно с
предварително
нулиране).
·
СМ – n-битов
комбинационен
суматор.
·
СФПр – Комбинационна
схема за
формиране на
признаците
на резултата.
·
РгПр – Регистър
на
признаците
(k-битов,
изграден от
еднотактни
тригери Latch-структура
).
·
ТП – Тригер на
преноса
(асинхронен
RS-тригер Latch-структура
с право
управление).
Чрез установяване
на този
тригер в
състояние “1”
се имитира
подаване на +1,
необходима
за формиране
на допълнителен
код.
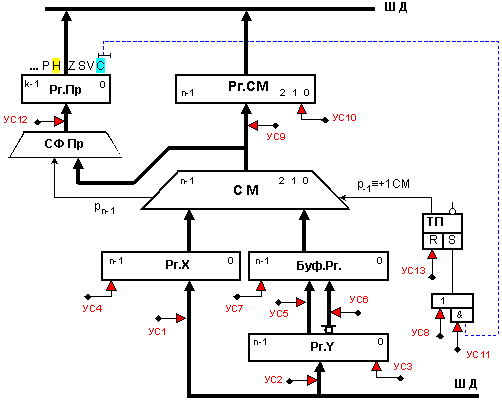

Фиг. 3.2.1.1.
Логическа
структура на
устройство за
събиране и
изваждане
с
комбинационен
суматор
В
логическата
структура е
реализирана
разрядна
мрежа с
дължина n[b].
След
операцията (Z=X+Y
или Z=X-Y) резултатът
е в
допълнителен
код и се
намира в
изходния
регистър РгСМ,
а неговите
признаци – в
регистъра на
признаците
на резултата РгПр.
Изходите на
тези два
регистъра са
подключени
към
данновата шина
ШД. Това
означава, че
те се
определят
като изходни
за
устройството.
Както е
показана и както
най-често на
практика се
реализира
тази шина, тя
е с
магистрална
организация.
Магистралната
организация
на връзките
между логическите
възли ще бъде
пояснена по-късно
тук в тази
глава. Ще
споменем
само, че нейната
реализация
изисква
употребата на
изходни
буфери с
трето
логическо
състояние (с
висок
изходен
импеданс).
Изходните буфери,
както и
тяхното
управление, в
тук представените
логически
структури
няма да бъдат
показвани.
Читателят
следва да
помни, че за
включване на
тези буфери
ще трябва да
бъдат
използвани
управляващи
сигнали от
тип “разрешение”
(Enable).
Резултатът
се
интерпретира
в светлината на
получените
за него
признаци.
Например, той
може да се
приеме за
верен, само
ако не е
настъпило
препълване.
Но както вече
беше
пояснено,
самото препълване
следва да се
интерпретира
според интерпретацията
на входните
комбинации.
Когато
обработваните
операнди се
интерпретират
като числа
със знак,
представени
в допълнителен
код,
признакът за
препълване V
се формира
според някоя
от
зависимостите
(1.6.2.18), (1.6.2.19) или (1.6.3.2).
Изборът на
една от тях е
конструктивен
въпрос. За
реализация
на избраната
функция към
схемата СФПр
трябва да
бъдат
изградени
съответните
логически
връзки.
Обикновено в
устройства с
комбинационен
суматор
най-често
реализирана
е
зависимостта
(1.6.2.19) – откриване
на препълване
чрез
преносите.
Стойността
на признака
за
препълване
се записва в
отделен
разряд на РгПр,
отбелязван
тук като бит V.
Когато
комбинациите
на входните
операнди се
интерпретират
като числа
без знак,
препълването
на
разрядната
мрежа се
разпознава с
помощта на
зависимост (1.2.3).
Според тази
зависимост
съдържанието
на РгСМ не е
вярно, ако
възникне
пренос от
старшия разряд
на суматора (pn-1=1).
Този факт
става явен в
края на
операцията благодарение
на това, че
преносът pn-1 се
записва в
разряд С (Carry
– пренос) на РгПр.
Фиксирането
на старшия
пренос в
отделен разряд
на регистъра
на
признаците позволява
в показаната
логическа структура
да се
реализират
модифицирани
варианти на
операциите
събиране и
изваждане,
наречени събиране с
пренос, изваждане
със заем. Модифицираните
варианти на
операциите се
реализират в
процесорите
като отделни
изпълними
операции. За
логическите
структури това
са операции,
които имат
свои
собствени алгоритми.
Тези
операции се
използуват в
случаите,
когато се
обработват
операнди, чиято
дължина е
по-голяма от
тази на
разрядната
мрежа.
Събирането
или
изваждането
на такива
операнди се
постига след
като те бъдат
разделени на
порции, които
имат
дължината на
разрядната
мрежа.
Съответните
порции на
двата
операнда се
обработват
при спазване
на тяхната
позиционност,
т.е.
започвайки от
младшата
порция в
посока към
старшата. Този
алгоритъм за
обработка се
нарича паралелно-последователен
и се
реализира
програмно.
Само
младшите
порции на
числата се
обработват с
основната
операция
(събиране или
изваждане).
Всички
останали
порции се
обработват с
модифицираната
операция
(събиране с
пренос или
изваждане
със заем), при
която за получаване
на резултата
се включва
възникналият
от
предходната
порция
пренос (или заем).
За целта в
логическата
структура на
предлаганото
устройство е
изградена
връзка, по
която
стойността
на признака С се
подава към
суматора. На
фигура 3.2.1.1 тази
връзка е
показана с
пунктир.
Тригерът на
преноса ТП
записва тази
стойност и я
подава за
събиране към
суматора по
входа на
младшия
пренос p-1.
В
логическата
структура от
фигура 3.2.1.1 всички
регистри
приемат
информация
за един такт,
което
означава, че
връзките между
тях са с
дължината на
разрядната
мрежа. Ако
разрядната
мрежа има
по-голяма
дължина от
ширината на
шината за
данни ШД,
то вместо
управляващите
сигнали УС1 и УС2
ще бъдат
необходими
няколко
управляващи сигнала
за
мултиплексиране
на входната шина
и приемане на
операндите
на порции.
Освен
признаците C и V,
чиято
същност и
предназначение
изяснихме в
глава 1, други
типични
числови
признаци още
са:
· Знак на
резултата S (sign). Този
признак по
същество
дублира
съдържанието
на
най-старшия
бит на
резултата, т.е.
РгПр[S]
:= СМ[n-1] , S = zn-1 .
Този бит
може да се
анализира
като знаков,
ако
съдържанието
на
разрядната
мрежа се интерпретира
като число
със знак.
·
Признаци
на
отношението. В
повечето
практически
случаи
алгоритмите
изискват да
се
проверяват
отношения
както между
знакови, така
и между беззнакови
стойности.
Отношенията
се декларират
явно и
резултатът
от тяхната
проверка се
определя
като "истина"
или “лъжа”,
т.е. като
логическа
стойност.
Фактически реализираното
отношение е
спрямо
числото нула.
Така най-често
проверяваните
отношения са:
1.
Резултат
равен на нула Z (Zero) – в
повечето
случаи този
признак
приема стойност
единица (Zero=1)
винаги,
когато
съдържанието
на изходния регистър
е равно на
нула. В
операции от
тип сравнение
обаче, както
ще стане ясно
по-късно,
този признак
ще се отнася
не за съдържанието
на изходния
регистър, а
за нефиксирания
резултат от
сравнението,
стоящ на
изхода на
суматора;
2.
Резултат
по-голям от
нула GT (Greather
Than);
3.
Резултат
по-малък от
нула LT (Less
Than).
Тези
признаци (и
други
подобни, за
отношения на
резултата спрямо
числото нула)
могат да не
бъдат формирани
в явен вид.
Обикновено
те се
получават като
стойности на
определени
логически функции,
включени в
състава на СФПр.
·
Признак
за четност на
резултата P (Parity). Стойността
на този
признак може
да се формира
при различна
интерпретация.
Обикновено
този признак
приема
стойност
единица (Р=1),
когато
резултата
съдържа
четен брой
единици. Този
смисъл на
признака
може да се
използва като
контролен
бит, показващ
правилността
на
предадените
данни.
Логическата
функция на
така
определения
признак (за
8-битов
резултат) е
следната:
![]() .
.
Оставяме
на читателя
задачата за
синтез и проверка
на тази
логическа
функция,
която от
всичките 256
възможни
комбинации
трябва да разпознава
само онези,
които
притежават
споменатото
качество.
·
Тетраден
пренос
(полупренос) H (Halfcarry).
Признакът за
възникнал
тетраден
пренос е типичен
пример на
признак за
собствена консумация.
Такива
признаци
обикновено
са програмно
недостъпни.
Използуват
се за
определяне
на 2/10-чната
корекция при
събиране на
2/10-чни числа. В
цифровите
процесори с
общо
предназначение
2/10-чната
аритметика е
частично
реализирана
и то само за
двуцифрени
операнди, при
които се
използват два
тетрадни
преноса – Н за
младшата
тетрада и С за
старшата
тетрада.
·
Други. Възможни
са и други
признаци или
комбинации
от
изброените.
Включването
им е в зависимост
от сферата на
приложение
на устройството
и от
конструктивните
му
особености.
Всеки
признак на
резултата се
формира като
стойност на
своята
собствена
логика,
реализирана
чрез
съответната
логическа
функция в
схемата СФПр. Така
например,
резултатът е
положително
число, ако
няма
препълване и
неговият
знак е положителен,
т.е.
![]()
и е
отрицателно
число, ако
няма препълване
и неговият
знак е
отрицателен,
т.е.
![]() .
.
В
разрядната
мрежа има
нула, когато
всички нейни
разряди
съдържат
нула, т.е.
![]()
Резултатът
е нула,
когато
всички
негови разряди
съдържат
нула и няма
препълване.
Признаците
на резултата
се
използуват
(консумират)
от алгоритмите
най-често
като условия
за различни
видове
условни
алгоритмични
преходи.
Някои от тях
могат да се
прилагат в
специфични
(помощни)
операции или
да удовлетворяват
определени
вътрешносхемни
потребности.
В реалните
процесори
управлението
на регистъра
на
признаците РгПр
е значително
по-сложно.
Сложността
се състои в
това, че
много от
признаците
се манипулират
самостоятелно,
т.е. всеки
отделен бит на
РгПр е обект
на отделни
операции,
което ще бъде
пояснено по-късно
в глава 5. С
използването
им на практика
читателят
може да се
запознае в книга [4].
Тук на фигура
3.2.1.1 е
показано, че
изходът на
регистъра на
признаците е
насочен към
данновата
шина. Това е
така, защото
съществуват
операции, при
които
съдържанието
на този
регистър се
запомня в
паметта заедно
с получения
резултат.
Това обаче не
е основното
транспортиране
на това
съдържание.
Както вече
беше споменато,
по-често то
се
разпространява
към устройствата
за
управление
хода на
изчислителния
процес. Това
става по
специални
връзки, които
не са
показани в
коментираната
структура.
Казаното
току що за
връзките на
регистъра на
признаците РгПр
се отнася за
всички
следващи
логически структури,
ето защо то
няма да бъде
повече повтаряно.
Функционирането на устройството при изпълнение на операция събиране и операция изваждане (виж фигура 3.2.1.1) може да се изрази с блок-схемата на микропрограмата, представена на фигура 3.2.1.2.
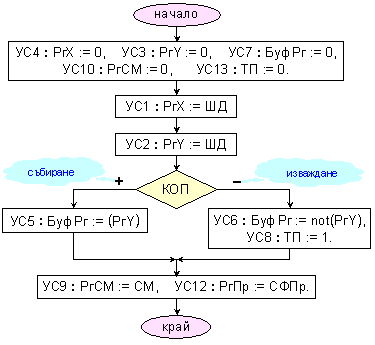
Фиг. 3.2.1.2.
Обединена
блок-схема на
микропрограми
за събиране и
изваждане
В
първия такт
на
микропрограмата
по управляващите
сигнали УС4,
УС3, УС7, УС10 и УС13
се нулират
всички
регистри с
изключение
на РгПр.
Така се
постига
изходното
състояние на
устройството.
След това
(втори и
трети такт) последователно
във входните
регистри се
зареждат
операндите –
първият в
левия
регистър РгХ
по сигнал УС1,
вторият в
десния РгY
по сигнал УС2.
В четвърти
такт, със
зареждането
на буферния
регистър БуфРг
по УС5 (или УС6 и
УС8),
суматорът СМ
започва да
формира
резултата, а СФПр
– признаците.
При операция
изваждане,
допълнителният
код на втория
операнд се
формира в
суматора от
съдържанието
на буферния регистър
и тригера на
преноса ТП.
В последния,
пети такт, в
изходните
регистри РгСМ
и РгПр по УС9
и УС12 се
фиксират
резултатът и
неговите
признаци.
Обединените блок-схеми на микропрограмите на модифицираните операции (събиране с пренос и изваждане със заем) са представени на фигура 3.2.1.3.
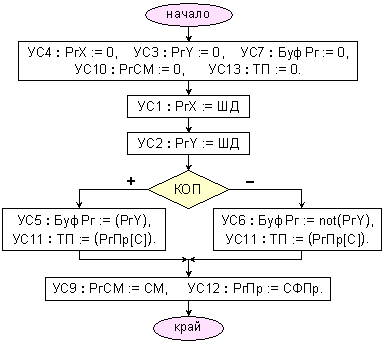
Фиг. 3.2.1.3.
Микропрограми
за събиране с
пренос и
изваждане
със заем
Според
тази
микропрограма,
заедно със
зареждането
на буферния
регистър БуфРг
по сигнал УС5
или УС6, се
зарежда и
тригерът на
преноса ТП
със
стойността
на бит С по
сигнал УС11. По
сигнал УС12 в
регистъра на
признаците РгПр
се записват
признаците
на получения
резултат. Тук
обаче следва
да обърнем
внимание на
актуалността
на получените
стойности на
отделните
признаци. В
смисъла на
операцията, актуален
е само бит С.
Ако с такава
операция се
обработват
междинни
порции от
операндите,
останалите
признаци са
неактуални.
Така
например в
този случай,
записаната в
бит V
стойност не
може да се
използва за
откриване на
препълване,
тъй като събраните
порции не са
най-старшите.
Тъй като
паралелно-последователната
обработка се
постига
програмно, то
отговорността
за правилното
тълкуване на
признаците
при всяка от
операциите,
носи програмистът.
Ако за
реализиране
на операция
събиране бъде
избран натрупващ
суматор, то
операцията
се извършва
между
неговото съдържание
и
постъпващият
на входа
втори операнд.
За
устройства с
натрупващ
суматор се
говори, че те работят
с резултата
от
предидущата
операция.
Ако първият
операнд на
операцията
не се съдържа
в
акумулатора,
т.е. той не е
резултат от
предходна
операция,
тогава се
налага предварително
да бъде
изпълнена
операция зареждане.
Логическата
структура на
устройство
за събиране и
изваждане,
основана на
натрупващ
суматор,
изисква
наличието на
входен регистър
за временно
съхранение
на втория операнд.
Резултатът
ще остане в
самия суматор.
Останалите
възли в
структурата
на устройството
са
аналогични,
но логиката
на схемата за
формиране на
признаците
на резултата СФПр
следва да
бъде
променена и
поставена в
съответствие
с логиката на
функциониране
на натрупващия
суматор. Този вид
суматори
читателят
може да изучи
от книга [2].
Най-специфичното
за него е
това, че
преносите
имат импулсен
характер.
Истинните
стойности на
преносите
съществуват
за кратко
време (по време
на “празния
такт”) и след
изпълнение
на операцията
не
съществуват
(вижте книга
[2]). Ето защо
формирането
и
фиксирането
на логическите
стойности в
бит С и бит V на РгПр,
които са
функции от
преносите,
трябва да бъде
съобразено с
това им
поведение –
използва се
зависимост
(1.6.2.19). В тази
връзка ясно
трябва да се
отбележи, че
за формиране
на признака
препълване
не е възможна
зависимостта,
използваща
знаците – (1.6.2.18),
тъй като след
изпълнение
на
операцията
първият операнд
(съдържал се
първоначално
в акумулатора)
не
съществува –
на негово
място се намира
резултата.
Логическата
структура на
устройство
за събиране и
изваждане,
основана на
натрупващ
суматор, е
показана на
фигура 3.2.1.4.
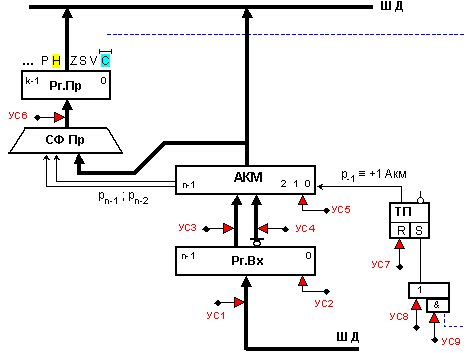
Фиг. 3.2.1.4.
Логическа
структура на
устройство
за събиране и
изваждане с
натрупващ
суматор
Логическата
структура
съдържа
следните логически
възли:
·
АКМ –
натрупващ
суматор,
съдържащ
първия
операнд
(n-битов, със
съсредоточена
логика).
·
РгВх –
регистър за
първия
операнд (n-битов,
изграден от
асинхронни
RS-тригери с право
управление,
структура Latch,
записващ
данни
еднофазно с
предварително
нулиране).
·
СФПр –
комбинационна
схема за формиране
на
признаците
на резултата.
·
РгПр –
регистър на
признаците (k-битов,
изграден от
еднотактни
тригери Latch-структура).
·
ТП
–
тригер на
преноса
(асинхронен
RS-тригер Latch-структура
с право
управление).
И тук този
тригер е предназначен
да осъществи
подаване на +1
към акумулатора
при
реализация
на
допълнителен
код или при
натрупване
на
съдържанието
на бит С.
Тук,
когато
представяме
първите
логически
структури на
операционни
устройства,
отново
искаме да
припомним на
читателя, че
те са
примерни, и
че техният
синтез е съобразен
със
специално
уговорените
преди това
предпоставки.
Казаното
за
подключването
на изходните
регистри към
данновата
шина на
устройството
от фигура 3.2.1.1
се отнася и
за това,
представено
на фигура 3.2.1.4 и повече
няма да бъде
повтаряно.
Микропрограмата
за
функциониране
на представената
логическа
структура е
показана на
фигура 3.2.1.5. В
нея, при
операция
изваждане, по
време на празния
такт, чрез
тригера на
преноса ТП и
управляващите
сигнали УС7 и
УС8, е реализирано
импулсното
подаване на (+1)
по входа на най-младшия
пренос.
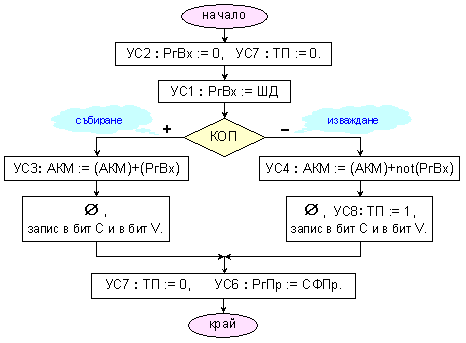
Фиг. 3.2.1.5.
Обединена
микропрограма
за събиране и
изваждане в
устройство
с натрупващ
суматор
В
представената
микропрограма
е прието, че
първият
операнд на
текущата
операция,
който е
резултат от предидущата
операция, се
намира в
акумулатора АКМ.
Така след
изчистване
на входния
регистър РгВх
чрез
управляващия
сигнал УС2 и
тригера на преноса
ТП – чрез
сигнал УС7, по
сигнал УС1
входният
регистър
приема втория
операнд.
Събирането
се извършва в
следващите
два такта,
когато чрез
сигнал УС3
или УС4 към
акумулатора
се подава
съдържанието
на входния
регистър или
неговото
отрицание
съответно.
Следва
празен такт,
който осигурява
разпространението
на преносите
в натрупващия
суматор. В
последния
такт се записват
признаците
на резултата.
Резултатът е
в
допълнителен
код и остава
в суматора.
В тази
логическа
структура,
така както и
в предидущата,
е възможно
изпълнение
на операциите
събиране с
пренос и изваждане
със заем.
Средствата
за това са
същите, но
управлението
им следва да
бъде
съобразено с
особеностите
на суматора.
Построяването
на блок-схема
на
микропрограмата
за тези
операции оставяме
на читателя.
В заключение може да се каже, че двете основни операции – събиране и изваждане налагат както за самото си изпълнение, така и за запомняне на резултатите, да се прилага инверсен код – обратен или допълнителен. Очевидно, ако се приеме обратен код за представяне на числата, то и изпълнението на операциите събиране и изваждане се налага да се извършва в обратен код; ако се приеме допълнителен код за числата, то и устройството трябва да работи в същия код. Използването на двата кода е еквивалентно както от гледна точка на апаратурните разходи за реализация на съответните логически структури, така и от гледна точка на тяхното бързодействие. Практиката обаче показва, че конструкторите отдават предпочитание на допълнителния код, въз основа на причини, които ние вече пояснихме.
В
представените
логически
структури се
използваше двувходов
суматор,
което е
традиционно
за тези
операции, тъй
като те в
чист вид са
двуместни.
Има обаче
алгебрически
изрази, в които
операндите
на
операцията
са повече от два,
например (а1+а2+
... +аn).
Изчисляването
на резултата
при
последователно
(натрупващо)
изчисление е
много бавен и
продължителността
му зависи от
броя на
операндите.
Преодоляването
на този
недостатък
може да се
постигне
когато се
постави
задачата за синтез
на суматор,
събиращ повече
от два
операнда едновременно.
Суматор с
повече от два
входа се
нарича концентратор.
С
изследването
и с решението
на тази задача,
както и със
синтеза на
такъв
суматор, читателят
може да се
запознае в книга [5]. Там
още е
представен и
синтезът на
конвейерен
умножител, в
който са
използвани
концентратори
(3:1), в резултат
на което се
повишава
бързодействието
на схемния
умножител
двойно в
сравнение с
традиционния,
при почти
същите
апаратни разходи.
Илюстрация
на
функционирането
на представените
логически
структури,
читателят
може да намери
в книга [2], където са
изложени
множество
примери за събиране
и изваждане
на различни
по знак и по
модул числа.
Примерите са
разписани в
пълно
съответствие
с
микропрограмите
и следователно
на тях следва
да се гледа
като неотменна
част от задълбоченото
изучаване на
изпълнимите
в цифровите
процесори
операции.
Следващият
раздел е:
3.2.2.
Операция
умножение ( Multiplication )