3.2.2.
Операция
умножение
Multiplication
Операция
умножение (Z=X.Y)
се дефинира
като производна
на операция
събиране.
Според това определение,
записът на
операцията X.Y
следва да се
разбира като
натрупваща
се сума от
множимото,
т.е. Z=X+X+...+X, в която
броят на
натрупванията
е равен на
количеството,
означено с
множителя Y
(зависимост (1.4.1)).
Тъй като за тази операция е в сила комутативният закон, то произведението може да се получи и чрез X-кратно натрупване на множителя, т.е. Z=Y+Y+...+Y. Разбира се, става дума за цели числа (с дясно фиксирана запетая).
Построяването на устройство за умножение въз основа на това определение следователно се свежда до устройство за събиране, в което се изпълнява натрупващо събиране, чийто алгоритъм може да бъде записан така
Z=0 ;
Z=Z+X ;
Z=Z+X ;
………
Z=Z+X .
Представеното
натрупване
(акумулиране)
по същество
се
организира
чрез
алгоритмична
структура
цикъл, от
вида с
предварително
известен
брой
повторения.
Такъв цикъл
се организира
с помощта на
изваждащ
брояч Бр,
чиято
начална
стойност е
множителят Y.
Условието за
край на този
цикъл е
равенството (Бр)=0 ?.
Организирана по този алгоритъм, операцията умножение има твърде разтегливо времетраене. Нейната продължителност се формира като многократна сума от продължителността на операция събиране. Кратността зависи от модула на множителя, който само в разрядна мрежа с дължина 1[B] се изменя от 0 до 255. Подобни силни колебания в продължителността на една и съща операция са крайно нежелателни, ето защо този алгоритъм практически не намира приложение. Той е полезен само с това, че доказва възможността за техническа реализация на тази операция.
За разработване на ефективен алгоритъм за умножение е необходимо да бъдат взети под внимание всички характеристики на операндите. Такива характеристики има две – първата се представлява от факта, че числата са представени в позиционна бройна система, а втората от факта, че това е двоичната бройна система. Така множителят може да се представи чрез полиномния си запис (зависимост (1.1.5)) и тогава произведението може да бъде записано както следва:
![]()
където
с yi са
означени
цифрите на
модула на
множителя,
записан в n-разрядна
двоична
мрежа като
число със знак
в прав код
(виж фигура 1.1.6.1.3).
Сумата (3.2.2.1) изразява същото произведение, но предлага друг начин за изчисление. Тази сума също е натрупваща, но нейните събираеми са винаги толкова на брой, колкото са разрядите на множителя или по-точно на цифровата част на разрядната мрежа, в която той е представен, ето защо нейното времетраене няма да зависи от модула на множителя.
Елементите
(X.yi) на сумата Z се
наричат поразрядни
произведения.
Всяко
поразрядно
произведение
следва да се
получи според
определението
за операция
умножение. В
случая,
когато
числата са
представени
в двоична
бройна
система,
възможните
поразрядни
произведения
са две: X.1=X и X.0=0.
Следователно
получаването
на
поразрядното
произведение
за всяка
цифра на
двоичния
множител се
свежда до
анализ на
тази цифра,
т.е. фактическото
изпълнение
на операция
умножение
като такова
липсва.
Всяко
поразрядно
произведение
от своя страна
е умножено с
тегловния
коефициент
на позицията,
на която то
съответства (2i). Тези
произведения
обаче могат
да бъдат получени
не по
определение,
а по
правилото на едно
следствие,
което е в
сила за
позиционни
бройни
системи. Според
това
следствие,
когато
множителят е i-кратен
на основата q
на бройната
система, произведението
запазва
значещите
цифри на множимото,
към които
отдясно се
дописват още i
на брой
незначещи
цифри нула.
Произведението
при този вид
на множителя
може да получи
чрез
логическо
изместване
на множимото
наляво на i
разряда. Така
и това
умножение не
се изпълнява
фактически, а
се замества
от изместване.
В крайна
сметка всяко
поразрядно
произведение
представлява
или нула или
изместеното
наляво на
съответния
брой разряди
множимо.
Окончателно,
след
направения
анализ става
ясно, че
сумата от
вида (3.2.2.1) ще се
получи вследствие
на операции
изместване и
събиране, организирани
в един
циклически
алгоритъм от
вида с
предварително
известен
брой
повторения.
Натрупването
на сумата (3.2.2.1)
може да бъде
организирано
на базата на
схемата на
Хорнер по два
начина: отдясно
наляво или
обратно. В
първия
случай се
формират
поразрядните
произведения,
започвайки
от младшите
цифри на
множителя в
посока към
старшите, а
във втория –
започвайки
от старшите
цифри на
множителя в
посока към
младшите.
Тези две организации представляват по същество двата основни метода за умножение:
·
умножение
с младшите
разряди
напред: ![]() ;
;
·
умножение
със старшите
разряди
напред: ![]() .
.
За
всеки от
методите за
умножение
могат да се
организират
по две схеми
за
натрупване, в
зависимост
от това, как
се постига
умножението
с тегловните
коефициенти.
Така например
при
умножение с
младшите разряди
напред
теглата на
позициите
следват във
възходящ ред,
което
означава, че
всяко
следващо
поразрядно
произведение
трябва да се
измества
наляво на
един разряд
спрямо
положението
на
предходното
поразрядно
произведение,
както е
показано на
схемата:
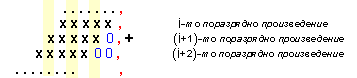
Това
означава, че
ако
междинната
сума в горната
схема е
неподвижно
число
(неподвижно спрямо
дясно
фиксираната
запетая), то
множимото
(представляващо
поразрядното
произведение)
трябва да се
измества
наляво. Описаната
организация
за натрупване
на
поразрядните
произведения
към
междинната
сума може да
се представи със
схемата от
фигура 3.2.2.1.
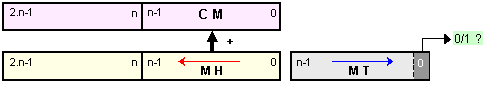
Фиг. 3.2.2.1. Схема
за умножение
с неподвижна
междинна
сума
Представената
организационна
схема е полезна
с това, че
позволява да
се оценят
предварително
апаратните
разходи за
реализация
на алгоритъма.
Така
например, ако
се реализира
схемата за
натрупване
на
междинната
сума, илюстрирана
по-горе, по
която ние сме
свикнали да
извършваме
ръчно
операция
умножение, полето
на
междинната
сума (в
крайна
сметка на
произведението)
трябва да е с
двойна
дължина, за
да може да
извършва
събиране
както в младшата
така и в
старшата си
част. Същото
се отнася за
полето на
множимото,
което за да
се натрупва
към
междинната
сума, трябва
да се
премества
спрямо нея
наляво.
Единственото
поле с
единична
дължина
съдържа множителя,
чийто
най-младши
разряд се
подлага на
анализ (0/1 ?). Тъй
като
логическата
връзка, излизаща
от този
разряд, не е в
състояние да
се премества,
то на
изместване
се подлага
самият
множител –
надясно.
Множителят (Мт) се измества надясно на един разряд, анализира се младшата му цифра, при което се взема решение за стойността на поразрядното произведение, което е 0 или равно на множимото (Мн). След това поразрядното произведение се прибавя към междинната сума. Отново се измества множителят надясно, а множимото наляво на един разряд и се анализира младшата цифра на множителя, за да се реши какво да се прибави към междинната сума. Тази съвкупност от микрооперации се повтаря толкова пъти, колкото са цифрите на модула на множителя, а те са (n-1) на брой. Обръщаме внимание на това, че използваните цифри на множителя след изместването се изгубват. След последния такт множителят изчезва – остава произведението с двойна дължина и множимото в лявата половина на своето поле.
Схемата
за
организиране
на операция
умножение от
фигура 3.2.2.1 определя
изказания
по-горе
алгоритъм,
който се
нарича алгоритъм
за умножение
по модул с
младшите
разряди
напред по
схемата с
неподвижна междинна
сума. Тази
схема
изисква за
своето
реализиране суматор
с двойна
дължина,
изместващ
регистър на
множимото с
двойна
дължина и
изместващ
регистър на
множителя с
единична
дължина.
Освен по тази организационна схема методът за умножение с младшите разряди напред може да бъде организиран по още една схема, в която неподвижно е множимото. Тогава, за да се реализира умножението на поразрядните произведения с тегловните коефициенти на позициите, на които съответстват, следва междинната сума да се измества надясно. Схемата на тази организация е представена на фигура 3.2.2.2.

Фиг. 3.2.2.2. Схема
за умножение
с неподвижно
множимо
В тази
организационна
схема се
повтарят (n-1) пъти
микрооперациите
анализ на
младшата цифра
на множителя,
натрупване
на поредното
поразрядно
произведение
и изместване
надясно на
един разряд
на множителя
и на
междинната
сума. Този
начин на умножение
се нарича алгоритъм
за умножение
по модул с
младшите
разряди
напред по
схемата с
неподвижно множимо.
Както
очевидно
може да се
прецени,
организацията
представена на
фигура 3.2.2.2, е
по-икономична
в сравнение с
тази от
фигура 3.2.2.1 – множимото
се съдържа в
регистър с
единична
дължина,
който при
това не е
изместващ. Нещо
повече,
схемата
предлага
допълнителна
възможност
за оптимизиране.
Тази
възможност
се състои във
факта, че по
същество
операция
събиране се
извършва само в
старшата
половина на
полето на
междинната
сума.
Следователно
младшата й
част съдържа
само
формираните
до момента
младши цифри
на
произведението,
които са
окончателни
и не се
променят при
следващите
събирания.
Това
означава, че
за реализиране
на младшата
половина на
междинната
сума не е
необходим
суматор, а
изместващ
регистър с
единична
дължина. Този
изместващ регистър
може да бъде
регистърът
на множителя,
тъй като
посоката на
изместване в
него е същата
и множителят
освобождава
старшите разряди
в регистъра,
които могат
да се заемат
от
удължаващата
се междинна
сума. След тези
съображения,
оптимизираният
вариант на
схемата за
умножение с
неподвижно
множимо има
вида от
фигура 3.2.2.3.
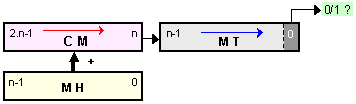
Фиг. 3.2.2.3.
Оптимизирана
схема за
умножение с неподвижно
множимо
Методът за умножение със старшите разряди напред натрупва поразрядните произведения, започвайки с най-значимите (най-старшите) позиции. Всяка следваща позиция има по-малък тегловен коефициент, т.е. редът им е низходящ. Ако приемем, че натрупващата се междинна сума записваме като резултат без да я изместваме, както правим обичайно при ръчно умножение, това означава, че всяко следващо поразрядно произведение е изместено надясно на един разряд спрямо предходното, което можем да изразим със следната схема:
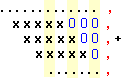
Описаната
организация
за
натрупване
на поразрядните
произведения
към
междинната
сума се
представя
със схемата
от фигура 3.2.2.4, от
където се
вижда, че за
изместващото
се надясно
множимо (Мн) е
необходимо
поле с двойна
дължина.
Първото
събиране се
изпълнява в
старшата
половина на
суматора, а
последното –
в младшата.
Ясно е, че
суматорът
трябва да
бъде също с
двойна
дължина.
Множителят
(Мт) се
измества наляво,
като
значещите
цифри, с
които се
получават
поразрядните
произведения,
се вземат от
най-старшия
разряд. След
умножението
множителят
се загубва.
В тази
схема се
повтарят (n-1) пъти
микрооперациите
изместване
наляво на
един разряд
на множителя
и на един
разряд на
дясно на
множимото,
анализ на старшата
цифра на
множителя и
натрупване
на поредното
поразрядно
произведение
в междинната
сума. Този
начин на
умножение се
нарича алгоритъм
за умножение
по модул със
старшите
разряди
напред по
схемата с
неподвижна
междинна
сума.

Фиг. 3.2.2.4. Схема
за умножение
с неподвижна
междинна
сума
Не е трудно да се забележи, че евентуалните апаратни разходи за реализация на тази организационна схема са еквивалентни на тези, съответстващи на схемата от фигура 3.2.2.1, т.е. при неподвижна междинна схема схемите по двата метода за умножение са еднакви.
По аналогия с метода за умножение с младшите разряди напред и тук може да се организира втора схема, в която относителното изместване на множимото спрямо междинната сума да бъде същото. При тази организация неподвижно е множимото, тогава наляво трябва да се измества междинната сума. Схемата ще изглежда както е показано на фигура 3.2.2.5.
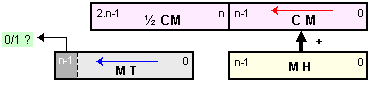
Фиг. 3.2.2.5. Схема
за умножение
с неподвижно
множимо
Съответната
последователност
от микрооперации,
реализиращи
операция
умножение в
тази схема,
се нарича алгоритъм
за умножение
по модул със
старшите
разряди
напред по
схемата с
неподвижно
множимо.
При
сравнение на
двете схеми
за организиране
на
умножението
по
разглеждания
метод се
вижда, че
втората
схема (фигура
3.2.2.5) е
по-икономична.
Това се дължи
на единичната
дължина на
полето на
множимото от
една страна и
на липсата в
него на
изместване
от друга
страна. При
по-внимателен
анализ може
да се
установи още
фактът, че
пълноценно
събиране в
схемата с
неподвижно
множимо се
извършва само
в младшата
половина на
суматора, а в
старшата се
разпространява
само
възможният
от младшата
половина пренос
pn-1. Това
позволява
старшата
половина на
междинната
сума да се
реализира с
допълнителна
икономия от
апаратурни
разходи,
благодарение
на
изпълнението
й чрез
полусуматор –
като броячна
схема.
Същността на
полусуматора
читателят
може да
намери в книга [2].
И така,
от всички
организационни
схеми на алгоритми
за умножение,
разгледани
до момента,
най-икономична
се оказва
третата –
представена
на фигура 3.2.2.3, ето защо
тя намира
най-широко
практическо приложение.
Внимание
заслужава и
петата
организационна
схема –
представена
на фигура 3.2.2.5,
реализираща
алгоритъм,
който както
ще се разбере
по-късно,
предлага
удобното й
обединяване
в обща
логическа
структура с
операция
деление.
Както
вече беше
показано,
произведението
е число,
което има
двойна
дължина и
когато
операция
умножение се
реализира в
съответствие
с избраната
организационна
схема,
препълване
не е възможно
да настъпи.
Това
означава, че
произведението
е представимо
число и
препълването
е принципно
невъзможно.
Една верижна
последователност
от операции умножение,
например от
тип
натрупващо
умножение
обаче
довежда до
динамично
изменение на
дължината на
получаваните
произведения,
което не може
да бъде
допуснато в
изчислителните
устройства.
Тази
особеност на операция
умножение, а
именно да
променя форматите
на
получаваните
резултати, е
уникална, а
данни с
динамично
променящи се
формати на практика
е невъзможно
да бъдат
поддържани. Ето
защо
обикновено
операция
умножение може
да се
изпълнява в
два режима: режим
на единична
дължина и
режим на
двойна
дължина на произведението. Под
режим на
единична
дължина
разбираме случай,
когато
операндите X
и Y, както и
резултатът Z,
се
възприемат
като числа,
побиращи се в
n-битови
регистри. Под
режим с
двойна дължина
разбираме
случая,
когато
операндите са
с единична
дължина, но
произведението
се приема с
двойна дължина.
Операнди с
двойна
дължина се
считат за невъзможни,
тъй като тази
дължина
надхвърля
първично
приетата за
разрядната
мрежа дължина
от n-бита,
която е
конструктивен
параметър за
техническото
средство.
В
режим на единична
дължина, при
умножение на
числа с дясно
фиксирана
запетая е
възможно да
настъпи
препълване,
ако старшата
половина на произведението
е различна от
нула. При
умножение на
числа с ляво
фиксирана
запетая положението
е
по-благоприятно,
тъй като възможната
за
изхвърляне
половина от
произведението
е младшата,
т.е. във
всички
случаи крайният
резултат,
възприеман
като
произведение,
следва да
включва
старшата
половина от резултата.
Произведение
с единична
дължина може
да се формира
чрез
закръгляне
до старшите n
разряда, при
запазване на
задоволителна
точност,
което не е
възможно при
числа с дясно
фиксирана
запетая.
В
режим на
двойна
дължина
както при
дясно, така и
при ляво
фиксирана
запетая
произведението
е
представимо,
но то следва
да се декларира
като число,
представяно
в друг
формат,
различен от
този на
съмножителите.
Тъй
като
дължината на
разрядната
мрежа е приета
равна на n[b], то
двойната
дължина е 2.n[b].
Модулът на
произведението
има дължина равна
на сумата от
дължините на
цифровите части
на съмножителите,
т.е. (n-1)+(n-1)=2.(n-1)[b].
Когато този
модул се
разположи в
двойния формат,
остават
свободни два
разряда, единият
от които е
предназначен
за знака на
произведението.
По
същество
съдържанието
на двойния
формат при
дясно
фиксирана
запетая е
следното:

Когато се умножават числа със знак в прав код, модулът на произведението се получава след умножение на модулите на съмножителите по един от четирите алгоритъма, а знакът на произведението се изчислява като стойност на логическата функция нееквивалентност:
![]()
И така,
синтезът на
логическата
структура на
устройство
за умножение
се определя
от избора на
един от
четирите
алгоритъма,
кратко
представени
по-горе. Тук,
по
разбираеми причини,
ние не сме в
състояние да
направим
това за всеки
един от тях. Ето
защо това ще
бъде
направено
само за най-икономичния
алгоритъм, а
именно
алгоритъма
за умножение
с младшите
разряди
напред и неподвижно
множимо,
чиято
организационна
схема е
представена
на фигура 3.2.2.3. Веднага
трябва да се
отбележи, че
възникват
две възможности
–
устройството
да се
основава на
логическата
структура за
събиране с
комбинационен
суматор
(фигура 3.2.1.1) или да се
основава на
логическата
структура за
събиране с
натрупващ
суматор
(фигура 3.2.1.4). Ще изложим
и двата
варианта.
Множество
числени
примери за
всеки от алгоритмите,
които ще
бъдат
изложени тук,
могат да
бъдат
разгледани в книга [2].
Ще добавим още някои съображения, касаещи операция умножение. Тъй като предполагаме за числата позиционна бройна система, определението (3.2.2.1) може да се запише чрез полиномния вид на числата както следва
![]()
Ако се приеме, че фактическият ред на двата полинома е k-ти и l-ти съответно, то редът на полинома на произведението е (k+l), т.е.
![]()
С други думи дължината на числото, представящо произведението е сума от дължините на числата на съмножителите. Ако се върнем към (3.2.2.1) технически дължината на формата на произведението нараства двойно. Следва да обърнем внимание, че форматът на резултата се изменя динамично, и че след няколко кратно умножение той може да драстично да се увеличи. В тази връзка трябва да отбележим, че все още не са известни изчислителни машини, които да поддържат динамични формати на данните. Това е проблем, който се стоварва върху раменете на Програмиста. Ето защо операция умножение, а както ще видим в последствие, и операция деление, са операции, към които той ще следва да се отнася изключително отговорно, ако иска да получава верни и точни резултати. Единственото средство в ръцете на Програмиста, с което той може да се предпази от тези проблеми, са операторите за деклариране на типа на променливите, което го задължава да познава или да предвижда правилно динамиката на междинните и на крайните числени резултати.
Следващият
раздел е:
3.2.2.1
Базова
логическа
структура на
устройство
за умножение,
основана на
комбинационен
суматор
( Basic
logical structure of a multiplication device based on a combination adder )