3.2.2.1 Базова логическа структура на устройство за умножение, основана на комбинационен суматор

Basic logical structure of a multiplication device based on a combination adder

Както вече беше обяснено, алгоритъмът за умножение по метода с младшите разряди напред по схемата с неподвижно множимо (оптимизиран вариант) по модул, е циклически от вида с предварително известен брой повторения. Основната част от логическата структура на бъдещото устройство за умножение, което синтезираме върху този алгоритъм тук, представлява структурата за операция събиране от вида с комбинационен суматор, която е представена на фигура 3.2.1.1. Към тази структура е необходимо да се добави един регистър за съхранение на множителя, който трябва да бъде изместващ надясно. За организиране на циклическото повторение е необходим изваждащ брояч и дешифратор за откриване на нулевото му съдържание. Разпознаването на нулевото съдържание на брояча ще използваме като условие за край на цикъла. Освен това е необходимо събирането да бъде натрупващо, с възможност за изместване надясно – както е показано на фигура 3.2.2.3.

В така избраната структура за събиране изходният регистър следва да се свърже с регистъра по левия вход на суматора, с което постигаме натрупването на междинната сума. Тази организация на натрупващо събиране е определена с разпределена логика (вижте книга [2]). В регистъра по десния вход на суматора е удобно да разположим неподвижното множимо, а за множителят е необходим отделен изместващ регистър.

В резултат на тези кратко изложени съображения и на известните ни предпоставки относно синтеза на логическите структури, устройството за умножение по избрания алгоритъм ще има логическата структура, представена на фигура 3.2.2.1.1.

В показаната логическа структура не са изобразени логическите възли и елементи на устройството за събиране, отнасящи се до признаците на резултата и до сигнала +1СМ. Тези елементи на структурата обаче са спестени единствено с цел да не се усложнява рисунката и ние винаги ще ги възприемаме като задължително присъстващи.

От фигурата се вижда, че регистрите на множителя РгМт' и РгМт", изградени от еднотактни RS-тригери (според посочените предпоставки), образуват изместващ регистър чрез косата връзка, управлявана от сигнала УС16, и правата връзка, управлявана от сигнала УС14. За постигане на двутактово изпълнение на микрооперация изместване правата връзка в този регистър е парафазна, т.е. броят на линиите в нея е двоен (2.n) (за всеки един вход на тригерите по една линия – съответно от прав и от инверсен изход). Същото се отнася за връзката между РгСм и РгХ, която се управлява от сигнала УС9. Парафазните връзки са неизбежни, когато микрооперация изместване се осъществява чрез двутактно управление. В противен случай тя се изпълнява за четири такта – една твърде крайна възможност, до която ние не желаем да достигаме. Натрупващата функция на устройството за събиране е реализирана чрез връзката между РгСм и РгХ, управлявана чрез сигнала УС9.

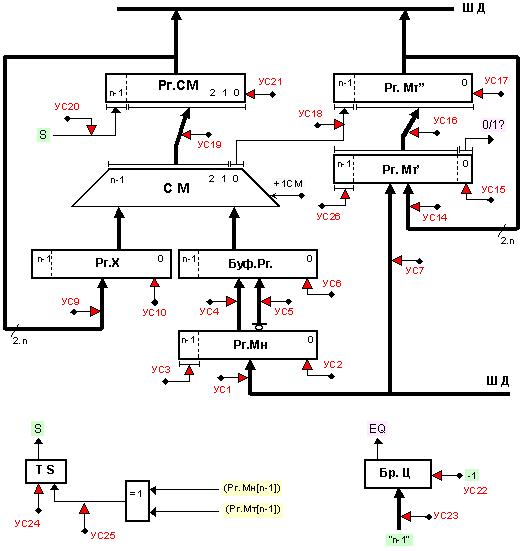
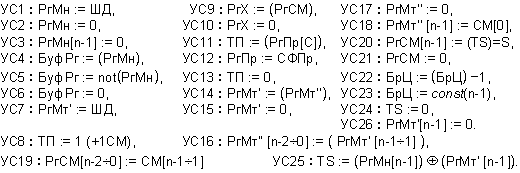
Фиг. 3.2.2.1.1. Базова логическа структура на устройство за умножение на числа представени в прав код по метода с младшите разряди напред по схемата с неподвижно множимо

Изпълнението на операцията започва с установяване на логическите възли в изходно състояние и приемане във входните регистри на двата операнда, представени в прав код. Правият код на числата разглеждаме като код, който е най-пряко свързан с формула (3.2.2.1), от която произлизат алгоритмите на операцията.

Изходното състояние на регистрите е нулевото съдържание, а началната стойност на брояча на цифрите БрЦ е константата (n-1), представляваща дължината на цифровата част на разрядната мрежа, т.е. броя на цифрите с които се умножава. След приемане във входните регистри на операндите, в схемата (=1) на функцията (3.2.2.2) се формира знакът на произведението, който и се запомня в тригера на знака ТS по управляващ сигнал УС25. Това запомняне е наложително, тъй като в края на операцията множителят не съществува, неговият знак е изхвърлен след последното изместване и формирането на знака на произведението в този последен момент е невъзможно. Междувременно, след консумиране на знаците на операндите, знаковите битове в съответните регистри се нулират – управляващи сигнали УС3 и УС12, в резултат на което в тях остават само модулите на числата. Така говорим, че същинското умножението фактически се изпълнява по модул. Изпълнението на алгоритъма за умножение в логическата структура от фигура 3.2.2.1.1 е изразено на фигура 3.2.2.1.2 чрез блок-схемата на микропрограмата.

Фиг. 3.2.2.1.2. Микропрограма за умножение на числа с ДФЗ представени в ПК в устройство с комбинационен суматор

Както може да се установи от микропрограмата, алгоритъмът за умножение на числа, представени в прав код, не използва всички управляващи сигнали, присъстващи в логическата структура от фигура 3.2.2.1.1. Това е така, тъй като тази структура ще бъде разглеждана като базова и върху нея ще бъдат пояснявани впоследствие и други алгоритми за умножение.

Окончателният резултат (произведението в прав код), се оказва в края на операцията разположено в изходните регистри - старшата част в РгСМ, а младшата част в РгМт".

В микропрограмата от фигура 3.2.2.1.2 могат да бъдат вложени допълнителни микрооперации, които могат да доведат до ускоряване на операцията при определени съчетания на съмножителите. Така например, след зареждане на всеки от операндите, може да се прави проверка на признака за равенство на нула - EQ. Ако за някой от операндите този признак е активен, то с това операцията може да завърши - резултатът е Z=0.

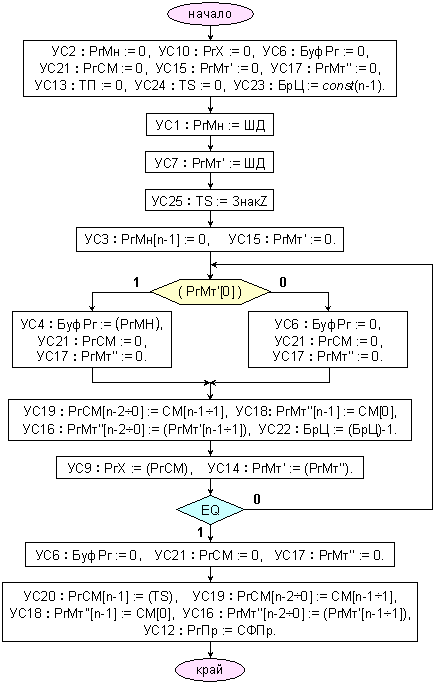
Логическата структура, която беше пояснена по-горе, е в състояние да умножава и числа с ляво фиксирана запетая. В този случай алгоритъмът завършва без последното изместване. Това се налага от лявата фиксация на запетаята, при което двойният формат на резултата има следния общ вид:

За да се осигури задължителната незначеща цифра, която в случая се намира в най-младшия разряд, при числа с ляво фиксирана запетая е необходимо да се нулират знаците на операндите преди началото на същинското умножение.

По-долу на фигура 3.2.2.1.3 е представена блок-схемата на микропрограмата за умножение по разглеждания алгоритъм на числа с ляво фиксирана запетая.

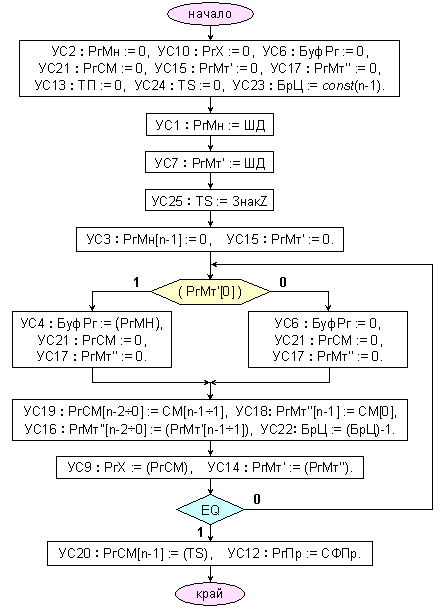
Фиг. 3.2.2.1.3. Микропрограма за умножение на числа с ЛФЗ представени в ПК в устройство с комбинационен суматор

Илюстрация на функционирането на представената базова логическа структура и изпълняваните в нея алгоритми, читателят може да намери в книга [2], където са изложени множество примери за умножение на различни по знак и по модул числа. Тези примери са разписани в пълно съответствие с разположението на логическите възли в структурата на устройството, както и в пълно съответствие с микропрограмите на алгоритмите и следователно на тях следва да се гледа като неотменна и специфична част от задълбоченото изучаване на изпълнимите в цифровите процесори операции.

По-късно, в книга [4], изучавайки машинните команди за умножение на реалния микропроцесор, читателят ще може да се убеди, че те изискват фиксирано разположение на операндите и резултата по съответните регистри на процесора, което е в пълно съответствие с изложеното по-горе, относно всички съображения на синтеза на логическата структура на устройството за умножение.

Следващият раздел е:

3.2.2.2 Базова логическа структура на устройство за умножение, основана на натрупващ суматор

Basic logical structure of a multiplication device based on a accumulator