3.2.3
Умножение
на числа,
представени
в допълнителен
код
Multiplication twos complement numbers
Вече бяха
пояснени
мотивите,
според които числата
с фиксирана
запетая е
удобно да бъдат
представени
в инверсен
код (вижте § 1.6).
Ето защо
вероятната
практическа
ситуация, в
която ще се
окаже операция
умножение, е
към нея да се
пристъпи със
съмножители,
представени
в инверсни
кодове - обратен или
допълнителен.
Тук ще се
ограничим и
ще
разгледаме
само
ситуацията,
когато
числата са в
допълнителен
код. Това обче
няма да
затрудни
читателят,
ако сам пристъпи
към
алгоритъма
за умножение
в обратен код
на числата.
И така, когато съмножителите са в допълнителен код, в тяхната цифрова част не винаги се намира модулът им, което означава, че разработените върху записа (3.2.2.1) алгоритми за умножение не могат да се приложат директно. Какво обаче все пак ще се получи, ако умножението се извърши върху допълнителните кодове чрез алгоритмите за умножение по модул, т.е.
![]()
Естествено,
желателно е,
така както и
при операция
събиране,
резултатът да
се получава в
допълнителен
код автоматично.
От
всички
възможни
случаи могат
да се формират
две групи
според знака
на множителя.
В първа
група са
случаите,
когато
множителят е
положителен,
т.е. Y>0.
Допълнителният
код на
множителя
при това
условие съвпада
с правия код,
т.е.
множителят е
представен
чрез цифрите
на модула си.
Тогава всички
поразрядни
произведения
ще се
изчисляват
правилно.
Всички
междинни
суми ще бъдат
натрупвани
също
правилно.
Това
натрупване
ще бъде
натрупване
на числа в
допълнителен
код,
независимо
от схемата,
по която ще
се изпълнява
умножението,
при което
всяко събиране
ще се
подчинява на
твърдението
(1.6.2.17). Двойната
дължина на
суматора в
схемите за
умножение
изключва
възможността
от препълване.
В крайна
сметка
произведението
ще се получи
по естествен
път в
допълнителен
код.
Втората
група
съдържа
всички
случаи, в
които
множителят е
отрицателен,
т.е. Y<0. При
това условие,
бидейки
представен в
допълнителен
код, цифрите
на множителя
не съответстват
на тези в
неговия
модул. Ако
приложим
обаче същия
алгоритъм за
умножение, ще
получим по
същество
произведение,
което не
съответства
на търсеното,
ето защо го
наричаме
псевдопроизведение.
Псевдопроизведението
е
произведение
на множимото
с онова, което
стои в
цифровата
част на
множителя.
Ако
множителят Y е
представен в
допълнителен
код, по
силата на
определението
(1.6.2.11),
последният
представлява
числото ( 2n-|Y| ).
Умножението
с него,
според (3.2.2.1), се
извършва
само с
цифрите от
цифровата му част, т.е. с
битове [ (n-2) ¸
0 ]. В
цифровата
част на
разрядната
мрежа се намира
числото ( 2(n-1)-|Y| ). Това число е
получено от
стойността
на кода чрез
премахване
на теглото на
знаковия разряд,
т.е.
![]()
Тогава
стойността
на
псевдопроизведението
може да бъде
записана
така
![]()
Внимателният
анализ на
полученият
за псевдопроизведението
израз
показва, че
истинското
произведение
Z се
съдържа в
него -
това е
умалителят в
разликата (3.2.3.1).
След тази констатация
псевдопроизведението
може да бъде
записано по
следния
начин:
![]()
и
ако на така
получения
запис се
гледа като на
уравнение с
едно
неизвестно - Z, то
неговото
решение е
![]()
В крайна
сметка
изразът (3.2.3.2)
изразява
начина, по
който може да
се получи
истинското
произведение,
ако вече е
получено
псевдопроизведението.
Tази последна
операция
изваждане се
нарича корекция.
В заключение може да се подчертае, че алгоритъмът за умножение в допълнителен код използва като първа част алгоритъма за умножение по модул, след което проверява какъв е знакът на множителя и ако той е бил отрицателен, завършва с корекцията (3.2.3.2). Произведението и в двата случая се получава в допълнителен код. Това ни дава основание да твърдим, че
![]()
По
принцип
полученият
алгоритъм
може да се
реализира и
за двата
метода на
умножение, при
това във
всяка от
четирите
възможни схеми
на
организация.
Тук обаче ще
бъдат разгледани
проблемите
на
реализацията
му само в
една -
тази, в която
се умножава с
младшите
разряди
напред при
неподвижно множимо
(фигура 3.2.2.3).
И така,
за
реализиране
на изказания
алгоритъм
може да бъде
използвана
логическата
структура на
устройството
за умножение
по модул,
показана на
фигура 3.2.2.1.1 или
тази, показана
на фигура 3.2.2.2.1.
Първата е
изградена
чрез
комбинационен
суматор, а
втората - чрез
натрупващ. За
да могат тези
две структури
да
реализират
алгоритъма
за умножение
в
допълнителен
код, те
трябва да
могат да реализират
операция
изваждане,
която е необходима
за осъществяване
на
корекцията
(3.2.3.2). Ето защо в
споменатите
логическите
структури са
реализирани
необходимите
логически
връзки и необходимите
управляващи
сигнали. В
структурата
от фигура 3.2.2.1.1
това е
връзката от
инверсните
изходи на
регистъра на
множимото РгМн
към буферния
регистър БуфРг,
управлявана
от УС5,
както и
сигнала +1СМ, който
се получава с
помощта на
управляващите
сигнали УС8 и УС13
(вижте фигура
3.2.1.1). Аналогично,
в
структурата
от фигура 3.2.2.2.1
това е
връзката от
инверсните
изходи на РгМн към АКМ,
управлявана
от УС5,
както и
сигналът +1АКМ,
реализиран
от
управляващите
сигнали УС7 и УС8 чрез
правия изход
на тригера за
пренос ТП
(вижте фигура
3.2.1.4).
Очевидно
е, че тези
допълнения
са незначителни,
а като се има
предвид, че
те съществуват
във всяко
устройство
за изваждане,
може да се
каже, че те са
отнапред
реализирани.
Реализацията
на
алгоритъма
за умножение в
допълнителен
код при
умножение с
младшите
разряди
напред по
схемата с
неподвижно множимо
създава
известни
проблеми,
свързани с микрооперация
изместване
надясно.
Същността на
проблемите
се състои в
това, че посоката
на
изместването
е
противоположна
на посоката,
в която се
разпространяват
преносите
при
формиране на
всяка
междинна сума
в суматора.
Първо е
необходимо
да се поясни,
че на
изместване
се подлага
число със
знак, т.е.
характерът
на
изместването
е аритметически.
Такова
изместване
надясно на
междинната сума,
при което
съдържанието
на знаковия разряд
се запазва,
се нарича аритметическо
изместване.
Тъй
като
циклическото
натрупване
на
междинната
сума се
извършва
между числа с
еднакви
знаци, то при
всяко
събиране е
възможно да
настъпи препълване,
а както беше
пояснено в § 1.6.,
при
препълване в допълнителен
код, знакът
на сумата се
разрушава,
или с други
думи в
знаковия бит
се оказва
цифра, която
не
съответства
на знака на
числото. Ето
защо при
настъпване
на препълване
е невъзможно
да се извърши
следващата
микрооперация
аритметическо
изместване.
Описаният по-горе проблем може да бъде решен по два начина.
Първият
начин е
свързан с
анализа на
ситуацията
около
знаковия разряд
на сумата при
препълване.
По принцип са
възможни две
ситуации
положително
и отрицателно
препълване. В
първата се
събират две
положителни
числа, а се
получава
отрицателна
сума, което е
илюстрирано
със следния
пример

Правилното изпълнение на аритметическото изместване надясно в този случай изисква възстановяване на знака в изместената сума. В този случай правилният знак е плюс и неговото значение съвпада със стойността на преноса от знаковия бит.
При отрицателно препълване се събират две отрицателни числа, а се получава положителна сума, което е илюстрирано със следния пример

И в този случай правилното изместване изисква възстановяване на знака в изместената сума, а той е минус. Може да се отбележи, че неговата стойност и в този случай съвпада със стойността на преноса от знаковия бит.
Така
може да се
обобщи, че когато
има
препълване
(V=1), изместването
не може да се
извършва със
запазване на
съдържанието
на знаковия
разряд,
защото той не
е истински.
Задачата
за
възстановяване
на знака е
задача за
синтез на
логическа
функция S, чиято
стойност
трябва да се
приема в
знаковия
разряд при
аритметическото
изместване
на
междинната
сума. За
целта трябва
да се обърне
внимание на
посочените
по-горе записи,
от които е
очевиден
изводът, че
при препълване
(V=1)
знакът на
сумата е
еквивалентен
на стойността
на преноса от
знаковия
разряд (
p(n-1) ). Следователно
в тези случаи
логическата
функция S е
конюнкцията
![]()
В случаите,
когато няма
препълване,
аритметическото
изместване
се извършва
със запазване
на знака, т.е.
стойността
на логическата
функция S се
определя от
конюнкцията
![]()
Окончателно
обединявайки
двата случая,
общият вид на
логическата
функция,
чиято стойност
ще определя
съдържанието
на знаковия
разряд при
изместване
надясно, е
следният:
![]()
Такова
изместване
надясно, при
което
знаковият
разряд на
числото се
определя от
стойността
на функцията
за
възстановяване
на знака (3.2.3.4), се
нарича модифицирано
аритметическо
изместване.
Тази
логическа
функция
следва да
бъде реализирана
в
логическата
структура на
устройството
за умножение
в
допълнителен
код и нейната
стойност да
бъде
подавана в
знаковия
разряд на
междинната
сума при
всяко нейно
изместване
надясно. При
това положение
можем да
направим
извода, че
става излишен
тригерът на
знака TS,
който
присъства в
базовите
логически
структури от
фигура 3.2.2.1.1 и
фигура 3.2.2.2.1,
както и свързаните
с неговото
управление
връзки и
управляващи
сигнали.
Вторият
начин за
възстановяване
на знака в
изместената надясно
междинна
сума се
основава на
свойството
на модифицирания
допълнителен
код да
запазва
знака на
сумата при
препълване. В
§1.6 беше
пояснено, че
знакът на
сумата при
препълване
се запазва в
левия бит на
знаковата
двойка
разряди. Това
дава
основание да
се твърди, че
ако изместването
надясно на
един разряд
се извършва
като чисто
аритметическо
изместване относно
разряда,
запазващ
знака, с това
проблемът на
изчезващия
знак е решен.
Това просто
решение се
вижда от
следните
примери за
двата случая
на
препълване:


Този начин за реализиране на аритметическото изместване изисква в посочените базови логически структури да се приложи модифициран допълнителен код за представяне както на множимото, така и на междинната сума. За целта дължината на възлите, свързани с реализиране на операция събиране трябва да бъде увеличена с един допълнителен разряд отляво.
Последното,
което трябва
да бъде
изяснено в
алгоритъма
за умножение
в
допълнителен
код, е как в
логическата
структура ще
се реализира
корекцията
(3.2.3.2).
Операцията
изваждане,
която
съответства
на тази
корекция, има
като
умаляемо
последната
междинна
сума, която
заема
всичките (2.n-1)
разряда от
полето на
произведението
отляво
надясно.
Преди
последното
изместване надясно
в най-десния
разряд на
полето на произведението
(виж фигура 3.2.2.3)
се намира
знакът на
множителя.
Използвайки
цитираната
организационна
схема,
ситуацията в
този момент може
да се изрази
със следната
схема:
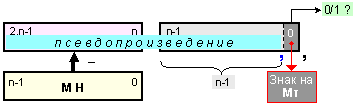
Фиг. 3.2.3.1.
Схема на
положението
на междинната
сума и
корекцията
в
която се
вижда, че
множимото се
оказва позиционирано
под старшите
разряди на псевдопроизведението.
С други думи,
относно
дясната
запетая на
псевдопроизведението,
съдържанието
на полето на
множимото може
да се
разглежда
като числото X.2(n-1).
Така
операция
изваждане
(изразяваща
корекцията
(3.2.3.2) във фигура
3.2.3.1) може да
бъде реализирана
непосредствено,
ако се налага.
Установяването
на тази
необходимост
става след
анализ на
най-десния
разряд на полето
на
междинната
сума, в което
към този момент
се съдържа
изместеният
след (n-1) такта
знак на
множителя,
т.е. неговата
най-старша цифра
yn-1.
След
последващо
изместване
надясно, произведението
избутва
ненужния
вече знак на множителя
и се оказва
окончателно
позиционирано
спрямо
десния край
на полето.
Реализацията
на цялостния
алгоритъм за
умножение на
числа с дясно
фиксирана
запетая,
представени
в
допълнителен
код, е напълно
възможно в
базовата
логическа
структура,
представена
на фигура 3.2.2.1.1.
Измененията,
които трябва
да бъдат
направени в
нея окончателно
са следните:
·
Трябва
да се
реализира
логическата
схема на
функцията за
възстановяване
на знака S,
чийто изход
да бъде подключен
към входа на
тригер РгСМ[n-1],
и нейната
логическа
стойност да
се записва в
този знаков
разряд при
всяка
изместване
на дясно;
·
Тригерът
на знака TS,
логическият
елемент
формиращ
знака на произведението,
както и
управляващите
сигнали УС24 и
УС25 стават
ненужни и
следва да се
премахнат;
·
Ненужни
стават и
управляващите
сигнали за
нулиране на
знаците на
съмножителите
УС3 и УС26;
·
Изобразената
инверсна
логическа
връзка от РгМн
към БуфРг,
управлявана
от УС5, която в
алгоритъма
за умножение
в прав код не
се използваше,
сега става
необходима,
тъй като чрез
нея се
реализира
операция
изваждане.
Изброените
конкретни
изменения
оценяваме
спрямо
общите
апаратни
разходи на
устройството
като много
малки по
обем, ето
защо си
позволяваме
да не
изобразяваме
новополучената
логическа
структура.
Микропрограмата
на
алгоритъма
ще се
реализира с
вече обявените
управляващи
сигнали.
В
случаите,
когато в
устройството
се умножават
числа с ляво
фиксирана
запетая,
изясненото
по-горе последно
изместване
след
корекцията
на псевдопроизведението,
не се
извършва. За
да се осигури
обаче
незначещата
нула в
най-младшия разряд
на
произведението
, е
необходимо
да се изтрие
оказалият се
там знак на
множителя. За
целта е
необходимо в
логическата
структура от
фигура 3.2.2.1.1 да
се въведе нов
допълнителен
управляващ
сигнал УС27,
чиято
функция да
бъде
микрооперация
нулиране, т.е. УС27 :
РгМт"[0]
:= 0.
И така,
в заключение
може да се
каже, че базовата
логическа
структура от
фигура 3.2.2.1.1 е в състояние
след
минимални
корекции да
реализират
алгоритъма
за умножение
в
допълнителен
код с
младшите
разряди
напред по
схемата с неподвижно
множимо.
Въпреки
че и
микропрограмата
на този алгоритъм
не се
различава
съществено
от тази, представена
на фигура 3.2.2.1.2,
тук на фигура
3.2.3.2 е приведена
блок-схемата
на
алгоритъма
за умножение
в
допълнителен
код в
структурата
с
комбинационен
суматор.
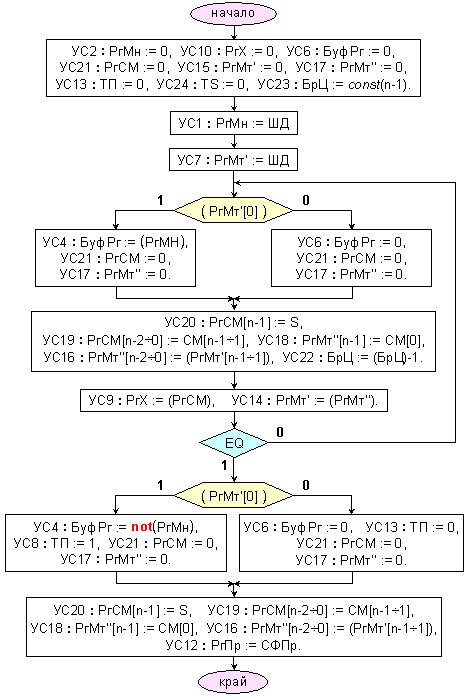
Фиг.
3.2.3.2.
Микропрограма
за умножение
на числа с
ДФЗ в ДК
в
устройство с
комбинационен
суматор
Реализацията
на цялостния
алгоритъм за
умножение на
числа с дясно
фиксирана
запетая,
представени
в
допълнителен
код, е възможна
в базовата
логическа
структура,
представена
на фигура 3.2.2.2.1.
Измененията,
които трябва
да бъдат
направени в
нея окончателно
са следните:
·
Акумулаторът
АКМ,
регистърът
на множимото РгМн
и
свързващите
ги логически
връзки
трябва да са
(n+1)-разрядни.
Това е
необходимо
за модифицирания
допълнителен
код;
·
Трябва
да се
реализира
логическата
схема за
чисто
аритметическо
изместване
на дясно. При
това
положение
управляващият
сигнал УС11
става
ненужен;
·
Тригерът
на знака TS,
логическият
елемент,
формиращ
знака на произведението,
както и
управляващите
сигнали УС19 и
УС20, стават
ненужни и
следва да се
премахнат;
·
Ненужни
стават и сигнали
за нулиране
на знаците на
съмножителите
УС3 и УС17;
·
Изобразената
инверсна
логическа
връзка от РгМн
към АКМ,
управлявана
от УС5, която в
алгоритъма
за умножение
в прав код не
се
използваше,
сега става
необходима,
тъй като чрез
нея се реализира
операция
изваждане.
Изброените конкретни изменения оценяваме спрямо общите апаратни разходи на устройството като много малки по обем, ето защо си позволяваме да не изобразяваме новополучената логическа структура. Микропрограмата на алгоритъма ще се реализира с вече обявените управляващи сигнали.
В
случаите,
когато в
устройството
се умножават
числа с ляво
фиксирана
запетая,
изясненото
по-горе
последно
изместване след
корекцията
на
псевдопроизведението,
не се
извършва. За
да се осигури
обаче незначещата
нула в най-младшия
разряд на
произведението,
е необходимо
след
извършване
на
корекцията
да се изтрие
оказалият се
там знак на
множителя. За
целта е
необходимо в
логическата
структура от
фигура 3.2.2.2.1 да
се въведе нов
допълнителен
управляващ
сигнал УС23,
чиято функция
да бъде
микрооперация
нулиране, т.е. УС23 :
РгМт"[0]
:= 0.
И така,
в заключение
може да се
каже, че базовата
логическа
структура от
фигура 3.2.2.2.1 е в състояние,
след
минимални
корекции, да
реализират
алгоритъма
за умножение
в допълнителен
код с младшите
разряди
напред по
схемата с
неподвижно
множимо.
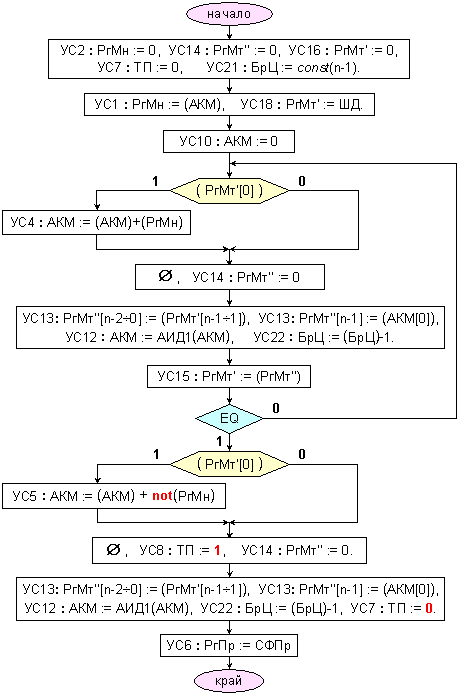
Фиг.
3.2.3.3.
Микропрограма
за умножение
на числа с
ДФЗ в ДК
в
устройство с
натрупващ
суматор
Реализирането
на
логическата
функция за възстановяване
на знака (3.2.3.4) в
структурата
на
устройство
за умножение в
допълнителен
код, основано
на натрупващ суматор,
е затруднено
от импулсния
характер на
преносите, а
така също и
от факта, че
истинските
стойности на
преносите не
съществуват
след
завършване
на
събирането.
Ето защо в
този случай
се
предпочита
модифицираният
допълнителен
код, в който
да са представени
множимото и
междинната
сума. В
резултат на
това
аритметическото
изместване
надясно се
извършва в
чист вид
спрямо
съдържанието
на n-тия бит
на
акумулатора.
По-горе,
на фигура 3.2.3.3, е
представена
микропрограмата
за
функциониране
на
устройството
за умножение
с натрупващ
суматор в
модифициран
допълнителен
код. В нея се
има предвид
структурата
и
управляващите
сигнали от
фигура 3.2.2.2.1,
като е взета
предвид
необходимостта
от n-ти
разряд в
акумулатора
и в регистъра
на множимото,
както и
аритметическото
изместване
относно
старшия n-ти
бит на
акумулатора.
Всичко
изложено
по-горе е
илюстрирано
с множество
числени
примери, с
които
читателят
може да се
запознае в книга [2].
Следващият
раздел е:
3.2.4 Умножение
по метода със
старшите
разряди напред ( Multiplication with the senior digits forward )