3.2.4 Умножение
по метода със
старшите
разряди напред
Multiplication with the senior digits forward
Операция
умножение по
този метод
може да бъде
организирана,
както вече
беше пояснено,
по два
начина: с
неподвижна
междинна
сума (вижте
фигура 3.2.2.4) и
с неподвижно
множимо
(фигура 3.2.2.5). Тъй
като по-икономичен
е вторият
вариант, тук
ще разгледаме
само
неговата
реализация,
при това само
в случая на
умножение по
модул, т.е. ще приемем,
че числата са
представени
в прав код.
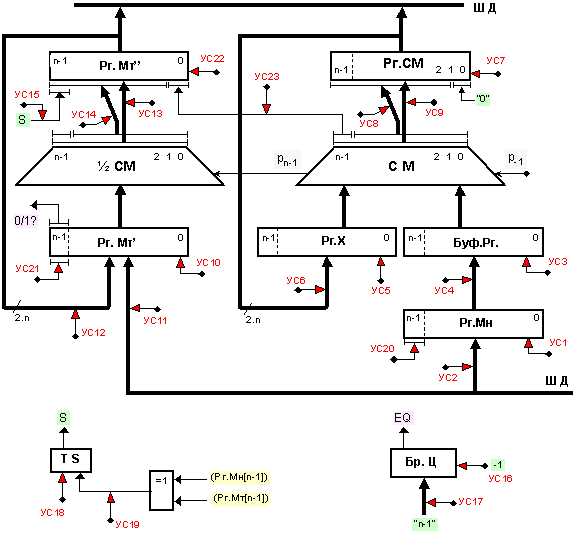
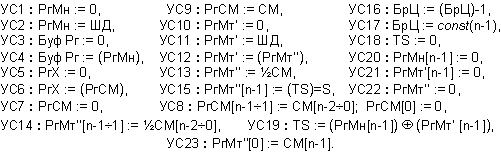
Фиг. 3.2.4.1.
Базова
логическа
структура на
устройство
за умножение
на числа
представени
в прав код по
метода със
старшите
разряди напред
по схемата с
неподвижно
множимо
Според алгоритъма за умножение с неподвижно множимо, последното се натрупва циклически след предварително изместване наляво на един разряд на множителя и междинната сума, които се поместват заедно в полето с двойна дължина. В логическата структура това са двата изходни регистъра, които в крайна сметка ще съдържат реазултата.
За реализация на алгоритъма е необходима логическа структура за събиране с натрупване, изместващ регистър за множителя, както и брояч на циклите. При синтеза на логическата структура на устройството за умножение по този алгоритъм ще се базираме на структурата за събиране с комбинационен суматор от фигура 3.2.1.1. Възможността за натрупване постигаме чрез обратната връзка от изходния регистър към входния регистър. Регистърът на множителя разполагаме отляво на множимото и използваме за съхранение на старшата част на междинната сума (произведението в крайна сметка). Останалите елементи на структурата – броячът за организиране на цикъла и елементите за формиране на знака на произведението, са аналогични на тези от вече разгледаните структури.
Всички
елементи на
синтезираната
логическа
структура са
съобразени с
приетите и обявените
от нас в
началото на
тази глава предпоставки
и водещи
критерии
относно вземаните
структурни и
схемни
решения.
Получената
логическа
структура е
представена по-горе
на фигура 3.2.4.1.
Този
алгоритъм
формално се
изразява със
следната
микропрограма,
представена
по-долу в
текстов вид с
помощта на
микрооператорите,
дефинирани в глава 2, §2.3.
0:: Начало // Текст на
микропрограма
за умножение
по
метода със
старшите
разряди напред
// ;
1::
УС1 :
РгМн := 0 ,
УС3 :
БуфРг := 0
, УС7 :
РгСм := 0 , УС22 : РгМт’’ := 0 ,
УС10 : РгМт’ := 0 , УС17 : БрЦ := n-1 , УС18 : TS := 0 ;
2::
УС2 :
РгМн := ШД=Мн ;
3::
УС11 :
РгМт’ := ШД=Мт ;
4::
УС19 : TS :=
ЗнакZ ;
5::
УС20 :
РгМн[n-1] := 0 ,
УС21 :
РгМт’[n-1] := 0
;
//
Изместване
наляво //
6::
УС14 :
РгМт’’[n-1¸1] := ½СМ[n-2¸0] , УС23 : РгМт’’[0] :=
СМ[n-1] ,
УС8 : РгСМ[n-1¸1] := СМ[n-2¸0] , РгСМ[0] := 0 , УС16 : БрЦ := (БрЦ)-1 ;
7::
УС12 :
РгМт’ := (РгМт’’) , УС6 : РгХ := (РгСМ) ;
// Проверка
на старшия
бит на
множителя //
8:: Ако (
РгМт'[n-1] )
то { УС4
:
БуфРг := (РгМн) , УС7 : РгСМ := 0 , УС22 :
РгМт’’ := 0
}
иначе { УС3 : БуфРг := 0 , УС7 : РгСМ := 0 , УС22 :
РгМт’’ := 0
} ;
//
Изместване
наляво //
9::
УС14 :
РгМт’’[n-1¸1] := ½СМ[n-2¸0] , УС23 :
РгМт’’[0] := СМ[n-1] ,
УС8 :
РгСМ[n-1¸1] := СМ[n-2¸0] ,
РгСМ[0] := 0
, УС16 : БрЦ := (БрЦ)-1 ;
//
Запомняне по
обратните
връзки //
10::
УС12 :
РгМт’ := (РгМт’’) , УС6 : РгХ := (РгСМ) , УС3 : БуфРг := 0 ;
//
Проверка на
условието за
край на цикъла
//
11:: Ако (not(EQ)) то {
Премини
към 8:: } ;
//
Умножение с
най-младшия
бит на
множителя //
12:: Ако (РгМт'[n-1]) то {
УС4 :
БуфРг := (РгМн) , УС7 :
РгСм := 0
, УС22 : РгМт" := 0 }
иначе { УС3
:
БуфРг := 0
, УС7 :
РгСм := 0 ,
УС22 : РгМт’’ := 0 } ;
//
Запис на
произведението
без
изместване наляво
и запис на
знака //
13::
УС9 :
РгСм := СМ
, УС13 :
РгМт’’[n-2¸0] := ½СМ[n-2¸0] , УС15 : РгМт’’[n-1]
:= (TS) ;
14:: Край ;
Алгоритъмът
за умножение
със старшите
разряди
напред може
да се
разработи и
за случаите,
когато
съмножителите
са
представени
в
допълнителен
код.
Реализацията
му обаче е
твърде
неикономична
поради това,
че за да се
получава
вярна сума,
множимото трябва
да се прибавя
във формат с
двойна дължина.
Ето защо
алгоритмите
за умножение
със старшите
разряди
напред по
принцип трудно
намират
приложение.
В книга
[2]
читателят
може да
намери
числени
примери, илюстриращи
функционирането
на алгоритъма
и на представената
логическа
структура.
Следващият
раздел е:
3.2.5
Алгоритми
за
ускоряване
на операция
умножение ( Algorithms for accelerating multiplication operation )