3.2.5.1 Алгоритъм на Бут (Booth)

Algorithm of Booth

Идеята за ускоряване, върху която е синтезиран този алгоритъм, се основава на възможността в множителя да се срещат компактни групи от еднакви цифри. Съществуват разнообразни реализации на алгоритъма както върху метода за умножение с младшите разряди напред, така и върху метода за умножение със старшите разряди напред. Тук обаче ние ще се ограничим само с варианта, който може да се реализира в базовите логически структури от фигура 3.2.2.1.1 или фигура 3.2.2.2.1.

И така, ако множителят Y=63 в двоична бройна система се представя с последователност от единици, например Y=111111, то за да се получи произведението Z=X.Y, според израза (3.2.2.1) трябва да бъдат извършени 6 събирания и 6 измествания - по едно за всяка единица от множителя.

Казаното може да се илюстрира още така: множителят Y представлява числото

а произведението е числото

Множителят Y=63 обаче може да бъде представен още по следния начин

и тогава произведението ще има вида

В последния израз за произведението се вижда, че то се получава като разлика от други две произведения, за чиито множители е характерно това, че съдържат в своите двоични еквиваленти само по една единствена единица. Последното наблюдение е твърде важно, тъй като то е в сила за всеки множител, който има описания първоначален двоичен вид независимо каква е дължината на групата от единици. С други думи, независимо колко са последователно следващите единици, количеството, което те означават може да се изрази чрез общата разлика

и двата елемента на която са двоични числа само с по една единица.

В заключение става очевидно как се ражда идеята за ускоряване на операция умножение - вместо да се извършват k на брой събирания и измествания, умножавайки с непосредствения вид на множителя, могат да се извършат само две събирания в допълнителен код и k на брой измествания. В изказаното току що съждение се има предвид, че поразрядните произведения с незначещите цифри на множителя са нули и тяхното натрупване не се извършва, тъй като е без значение за междинната сума.

Тъй като приехме да разглеждаме умножението с младшите разряди напред по схемата с неподвижно множимо, при всяка среща на значеща цифра (1) в множителя, може да се предполага, че тя е начало на група от единици, които се редят до нея в посока на старшите позиции на множителя. Тъй като при умножение с младшите разряди на множителя напред, поразрядните произведения се натрупват във възходящ ред на теглото което имат, то операциите които следват от израза (3.2.5.1.1), се извършват в точно определен ред: първо операция изваждане, т.е. натрупване на елемента (-Х.1) и след това операция събиране (+Х.100...0). Второто поразрядно произведение естествено се изпълнява не буквално, а след k на брой измествания, като (+Х.1), т.е. когато се достигне края на групата от значещи цифри. При последователното анализиране на цифрите на множителя в посока от младшите към старшите, краят на групата от единици се установява при среща на незначеща цифра, т.е. (0).

И така, за реализация на алгоритъма на Бут в метода за умножение с младшите разряди напред по схемата с неподвижно множимо трябва да се откриват началото и краят на всяка група от единици. В началото на всяка такава група се извършва операция изваждане на множимото, а в края на групата - операция събиране на множимото. Във всички останали тактове се изпълнява само изместване.

С изказаното току що завършва анализът на идеята и синтезът на новия алгоритъм. Следва да изясним неговата реализация. Тъй като определянето на поредната операция за натрупване към междинната сума вече не зависи единствено от текущия бит на множителя, то е необходимо да се синтезира нова логическа функция, която да поеме това задължение.

За да се разпознава началото и края на групите от последователни единици, е необходимо във всеки отделен такт да се анализира стойността на поредната цифра на множителя y_i в зависимост от предходната и вече обработена по-младша y_i-1. С променливата i=0,1,2,3, … (n-1) в случая е означен номерът на поредния бит, но той може да се отъждестви и с номера на поредния такт. Възможните при сравнението на двете цифри ситуации са четири и необходимите за тяхното правилно интерпретиране микрооперации се определят по следния начин:

Комбинацията 00 в дадения i-ти такт означава, че се намираме във вътрешността на група от незначещи цифри на множителя (...000...) и следва да изпълним само изместване, т.е. пропускаме операция;

Комбинацията 10 в дадения i-ти такт означава, че срещнатата значеща цифра може да се окаже начало на група от следващи я единици. В този случай трябва да изпълним изваждане на множимото от междинната сума, след което да изпълним изместване.

Комбинацията 11 в дадения i-ти такт означава, че се намираме вътре в група от значещи цифри на множителя (...111...) и следователно, докато не достигнем нейния ляв край, трябва да изпълняваме само изместване.

Комбинацията 01 в дадения i-ти такт означава, че при движението към старшите разряди на множителя сме достигнали левия край на група от единици и трябва да изпълним операция събиране, която заедно с вече отпреди изпълненото изваждане според израза (3.2.5.1.1), да формира правилното произведение с групата от единици. След събирането се изпълнява изместване.

Разпознаването на всяка от тези ситуации и назначаването на необходимите микрооперации се извършва с помощта на две логически функции: c_i - функция на изместването и s_i - функция на операцията. Смисълът на тези две функции се определя чрез кодирането им по следния начин:

(3.2.5.1.2)

След така уговореното съответствие между логическите стойности и смисъла, функциите имат стойности, посочени в таблицата на истинност (таблица 3.2.5.1.1).

Таблица 3.2.5.1.1 Функции на Бут

c_i	c_i	c_i	s_i
0	0	0	* , стойността на функцията е без значение (не се назначава операция)
0	1	1	0 , определя операция събиране (+)
1	0	1	1 , определя операция изваждане (-)
1	1	0	* , стойността на функцията е без значение (не се назначава операция)

От таблицата на истинност следва аналитичният вид на тези логически функции:

Базовите логически структури от фигура 3.2.2.1.1 и тази от фигура 3.2.2.2.1, могат лесно да бъдат пригодени към изискванията на алгоритъма на Бут. За целта регистърът на множителя РгМт трябва да се разшири отдясно с още един разряд с №(-1), в който да се съхранява след изместване обработената в предходния такт цифра на множителя y_i-1. Така неговата дължина става (n+1) бита. Началната стойност на този разряд трябва да бъде нула, т.е. РгМт[-1]:=0. Управляващото устройство реализира алгоритъма на Бут като подава управляващите сигнали така, че да се реализират на всеки такт изискванията на функциите c_i и s_i. Тази част на регистъра на множителя ще има следния вид:

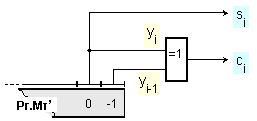
Фиг. 3.2.5.1.1. Логически функции на Бут

Тъй като в получения алгоритъм се изпълнява както операция събиране, така и операция изваждане, той е много удобен за умножение на числа със знак, представени в допълнителен код. Произведението се получава в допълнителен код и в този смисъл тригерът на знака TS и свързаните с него логическа схема и управляващи сигнали стават ненужни.

Алгоритъмът на Бут има един недостатък, който се изразява в това, че при определено съчетание на цифрите на множителя вместо да намалява броя на аритметичните операции, той ги увеличава, което може да доведе в някои структурни реализации до цялостно забавяне на умножението. Такава ситуация настъпва във всеки участък от множителя, където се редуват цифрите 0 и 1. Например, когато се умножава по класическия алгоритъм с множителя Y=10101=21, ще бъдат извършени три операции събиране, съответстващи на трите значещи цифри в двоичния еквивалент на множителя. Когато обаче се умножава по алгоритъма на Бут, всяка срещната единица ще се интерпретира като начало на група от единици и ще се назначава операция изваждане, а всяка срещната нула ще се интерпретира като край на групата от единици и ще се назначава операция събиране. В резултат на това ще се изпълнят два пъти повече събирания в допълнителен код. Казаното може да се илюстрира със следната схема:

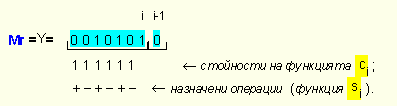
Според класическия алгоритъм се извършва натрупването:

Z = X.Y = X.21 = 0 + X.1 + X.4 + X.16 ,

а според алгоритъма на Бут при този множител натрупването е:

Z = 0 - X + X.2 - X.4 + X.8 - X.16 + X.32 = X.21.

Резултатът, както може да се види, е същият, въпреки че назначените операции са 2 пъти повече! Това обаче не винаги води до фактическа реализация на закъснение в изпълнение на умножението. За логическа структура, в която операция събиране се побира в рамките на един такт, този факт е без значение. Нещо повече, при тази интерпретация на цифрите на множителя, която се определя от функциите (3.2.5.1.3), не е възможно в нито един такт на циклическото натрупване да настъпи необходимост от аритметическо събиране. Това означава, че препълване при събиране е принципно невъзможно да настъпи, в резултат на което всички измествания могат да се изпълняват в чист аритметически вид. Казаното до момента се отнася само до случаите, когато числата са представени в прав код, т.е. умножението е по модул.

Когато обаче прилагаме този алгоритъм върху числа представени в допълнителен код, съществува едно изключение. Изключението се получава винаги, когато множимото е най-малкото за разрядната мрежа число, т.е.

Ако множителят е различен от нула, то започвайки умножението с младшите разряди напред, първата срещната единица ще назначи операция изваждане. Тъй като натрупаната междинна сума до този момент ще бъде нула, изваждането на това отрицателно множимо ще доведе до неизбежно препълване.

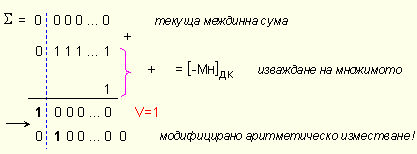
В горния пример най-малкото числов допълнителен код е записано по определение

[·]_дк = [·]_ок+1.

Препълването е неприятен факт, и тъй като той може да настъпи във всеки разряд, то се налага изместванията надясно да се реализират като модифицирани аритметически, т.е. с приложение на функцията за възстановяване на знака (3.2.3.4). Това изключение е илюстрирано в [1, пример №58], а така също и в [2, пункт 4, фигура 4.12].

В заключение ще отбележим, че реално намаляване на времетраенето на операция умножение може да бъде постигнато в случаите, когато продължителността на микрооперация събиране е по-голяма от тази на изместване, а така също и в случаите на асинхронно управление на логическата структура. Алгоритъмът на Бут не е подходящ за реализация в устройство с натрупващ суматор поради наличието на празен такт при събиране. В случаите, когато всеки такт на управляващото устройство е с постоянна продължителност (синхронен метод на управление), изпълнението на едно умножение по метода на Бут продължава точно толкова, колкото и по класическия алгоритъм.

Алгоритъмът на Бут може да бъде реализиран в базовата логическа структура за умножение по метода с младшите разряди напред (фигура 3.2.2.1.1). Измененията, които следва да се реализират върху тази структура вече бяха пояснени. По обем те са минимални, поради което тук не представяме съответната структура. По-долу следва микропрограмата за умножение по алгоритъма на Бут в базовата логическа структура от фигура 3.2.2.1.1, в която се има предвид, че са реализирани споменатите по-горе изменения.

0:: Начало // микропрограма за умножение по алгоритъма на Бут

на числа представени в допълнителен код // ;

1:: УС2 : РгМн := 0 , УС6 : БуфРг := 0 , УС10 : РгХ := 0 , УС21 : РгСМ := 0 ,

УС15 : РгМт’ := 0 , УС17 : РгМт’’ := 0 , УС13 : ТП := 0 , УС23 : БрЦ := n ;

2:: УС1 : РгМн := ШД=Мн ;

3:: УС7 : РгМт’ := ШД=Мт ;

4:: Ако ( c_i ) то // следва операция //

{ Ако ( s_i ) то // следва операция изваждане //

{ УС5 : БуфРг := not(РгМн) , УС8 : ТП := 1 = +1СМ ,

УС21 : РгСМ := 0 , УС17 : РгМт’’ := 0 } ;

иначе // следва операция събиране //

{ УС4 : БуфРг := (РгМн) , УС13 : ТП := 0 ,

УС21 : РгСМ := 0 , УС17 : РгМт’’ := 0 } ; }

// изместване //

5:: УС20 : РгСМ[n-1] := S , УС19 : РгСМ[n-2 0] := СМ[n-1 1] , УС18 : РгМт’’[n-1] := СМ[0] ,

УС16 : РгМт’’[n-2 ¸ -1] := (РгМт'[n-1 ¸ 0]) , УС22 : БрЦ := (БрЦ)-1 ;

6:: УС9 : РгХ := (РгСM) , УС14 : РгМт’ := (РгМт’’) ;

7:: Ако ( not(EQ) ) то { Премини към 4:: } ;

8:: Край ;

Както може да се види от микропрограмата, този алгоритъм може да се определи като хомогенен, тъй като той обработва еднакво както цифровата част на множителя, така и знаковия разряд. Числени примери, илюстриращи функционирането на представената логическа структура и на алгоритъма, читателят може да намери в книга [2].

Следващият раздел е:

3.2.5.2 Алгоритъм на Леман (Lehman) ( Algorithm of Lehman )