3.2.5.3.1
Умножение с
два разряда
едновременно
в
допълнителен
код
(с младшите
разряди
напред)
Multiplication
with two bits at the same time in two’s complement
(with the juniors ahead)
Както вече беше обърнато внимание в предидущия пункт, алгоритъмът за умножение с два разряда едновременно е удобно да се реализира върху числа представени в допълнителен код. Процесът на умножение протича за всяка двойка разряди на множителя в пълно съответствие с таблица 3.2.5.3.1, включително и в последния такт, стига множителят да е положително число. В случаите когато множителят е положително число, умножението завършва нормално, в съответствие с таблицата и произведението се получава в допълнителен код. Както беше изяснено в пункт 3.2.3, когато числата са в допълнителен код, получаването на произведението е с едно изключение - случаите на умножение с отрицателен множител. Тогава натрупаната сума определихме като псевдопроизведение. Аналогично на случая на последователно умножение и тук е необходимо да бъде реализирано съответно правило за корекция на псевдопроизведението.
В
последния
такт
двойката
цифри е
съставена от
знака на
множителя yn-1 и
неговата
най-старша
цифра yn-2. Тук се
предполага,
че броят на
разрядите на
множителя (n) е
четен.
Следователно
в последния такт
е необходимо
да се следи
дали последната
двойка
разряди
представляват
число, което
е равно или
по-голямо от 2, което
ще означава,
че
множителят е
отрицателно
число.
Операцията,
която трябва
да се назначи
в последния
такт при
отрицателен
множител,
зависи от
възможните
комбинации
от стойностите
на
разглежданите
параметри.
Проблемните
комбинации в
случая на
отрицателен
множител в
този
последен
такт, когато
на анализ са
подложени
неговите два
най-старши
бита, са
показани в
следната
таблица.
Таблица
3.2.5.3.1.1
Определяне
на
операцията
|
|
|
|
операция |
|
0 |
1 |
0 |
-2.X |
|
0 |
1 |
1 |
-X |
|
1 |
1 |
0 |
-X = -2.X+X |
|
1 |
1 |
1 |
+0 = -X+X |
Назначените
за
изпълнение в
последния такт
операции за
случаите от
таблица 3.2.5.3.1.1 са
определени
въз основа на
алгоритъма за
умножение в
допълнителен
код. Според
този
алгоритъм
умножението
завършва с
корекция на
псевдопроизведението,
определена чрез
израза (3.2.3.2).
Ще
докажем
резултантната
операция (-2.X) за
комбинация (010), която
е посочена
първа в
горната
таблица. Ще
отбележим в
началото, че
това е
случай, в
който
междинната
сума е
формирана
без грешки, тъй
като
функцията на
корекцията K(t-1)=0. Според
класическия
алгоритъм за
умножение в
допълнителен
код,
окончателното
произведение
при
посочените
две
най-старши
цифри на
множителя yn-1=1 и yn-2=0 ще бъде
формирано в
резултат на
следните действия:

Изразът, съответстващ на горе описаните действия, може да се запише и преобразува по следния начин:
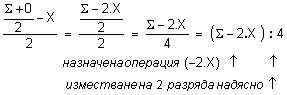
Така
получения
вид на израза
може да се
интерпретира
с действията
в алгоритъма
за умножение
с два разряда
едновременно.
Както е
посочено в
схемата (и в
първия ред на
горната
таблица)
назначаваната
в случая
операция е -2.Х,
след което
следва
последното
изместване
надясно на
два разряда.
Полученото
произведение
е в
допълнителен
код.
Аналогично
се определя
резултантната
операция за
втората
комбинация
от таблицата - (011),
указваща
умножение с
отрицателен
множител,
(значеща
цифра в старшия
разряд yn-1=1), което
трябва да се
изпълни без
корекция от
предидущия
такт K(t-1)=0. Според
класическия
алгоритъм за
умножение в
допълнителен
код,
окончателното
произведение
при
посочените
две
най-старши цифри
на множителя yn-1=1 и yn-2=1
ще бъде
формирано в
резултат на
следните
действия:

Изразът, съответстващ на горе описаните действия, може да се запише и преобразува по следния начин:
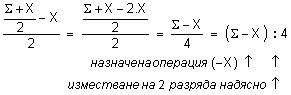
Така
полученият
вид на израза
може да се интерпретира
с действията
в алгоритъма
за умножение
с два разряда
едновременно.
Както е
посочено в схемата
(и във втория
ред на
таблица 3.2.5.3.1.1)
назначаваната
в случая
операция е -Х,
след което
следва
последното
изместване
надясно на два
разряда.
Полученото
произведение
е в
допълнителен
код.
Резултантните
операции в
последните
два случая на
таблицата - (110)
и (111)
се получават
въз основа на
операциите
от първите
две
комбинации,
но с
допълнително
отчитане
теглото на
коригиращата
функция K(t-1)=1, която
след изместването
в този такт
има тегло
равна на +X.
С казаното до момента считаме, че алгоритъмът за умножение по метода с младшите разряди напред с 2 разряда едновременно в допълнителен код е изложен. Последните забележки, които ще представим по-долу, се отнасят до апаратната реализация на алгоритъма въз основа на базовата логическа структура от фигура 3.2.2.1.1. Анализирайки операциите от таблица 3.2.5.3.1 и таблица 3.2.5.3.1.1, се вижда, че реализирането им изисква построяването на четири вида връзки от регистъра на множимото към суматора, а именно:
-
пряка права
връзка за
реализация
на операция
събиране: +X ;
-
пряка
инверсна
връзка за
реализация
на операция
изваждане: -X ;
- коса
наляво права
връзка за
реализация
на операция
събиране: +2.X ;
- коса
наляво
инверсна
връзка за
реализация
на операция
изваждане: -2.X .
Това
разточителство
на връзки
може да бъде
избегнато,
ако в
суматора
освен
веригата за
изместване
на 2 разряда
едновременно
се изгради и
верига за
изместване
на един
разряд.
Такава
верига може
да се окаже
необходима и
за други
операции,
така че тя
може дори да
се счита за
съществуваща.
Тогава
натрупването
на
поразрядните
произведения
+2.X и -2.X може
да се
реализира
по-лесно чрез
преките (права
и инверсна) връзки
между
суматора и
регистъра на
множимото
при
предварително
изместване
на междинната
сума на един
разряд
надясно в случаите,
когато са
назначени
тези
операции. Натрупването
на
поразрядните
произведения
в такива
случаи
завършва с
още едно допълнително
изместване
на
междинната
сума на един
разряд
надясно.
Тук ние не
представяме
логическата
структура на
устройство
за умножение
с два разряда
едновременно.
Тази
логическа
структура,
както и
съответната
за нея
микропрограма,
оставяме
като задача
за самостоятелна
работа на
читателя.
Представените
в предидущите
пунктове
решения
могат да бъдат
пример за
търсеното
тук решение.
Илюстрация
на
алгоритъма
чрез
подходящи
числени примери
читателят
може да
намери в книга [2].
В
заключение
може да се
обобщи, че
този метод на
умножение
съкращава
продължителността
на операция
умножение,
тъй като
обработва по
две цифри от
множителя на
такт. Може да
се приложи за
числа без
знак, за
числа със
знак в прав
код, както и
за числа със
знак в допълнителен
код.
Отделните
алгоритми имат
минимални
различия,
които се
отнасят до
действията в
последния
такт, когато
старшата
цифра на
множителя
може да се
интерпретира
или като
значеща
цифра или
като знак на
множителя.
Алгоритъмът
намира
широко
приложение в
аритметичните
устройства,
както и в
специализирани
интегрални
схеми.
Следващият
раздел е:
3.2.5.4
Умножение с
два разряда
едновременно
(със старшите
разряди
напред)
Multiplication with two bits at the same time (with the senior forward)