3.2.5.5 Алгоритъм на Мак’Сорли

Algorithm of Mac'Sorley

В последно време в схемните умножители широко разпространение намира алгоритъмът за умножение на два разряда едновременно, модифициран чрез алгоритъма на Бут, (автор на този алгоритъм е Мак’Сорли). Предимствата на алгоритъма на Бут вече бяха изяснени. След запознаване с алгоритмите за умножение с два разряда едновременно естествено възниква интересът за изследване на възможността за тяхното съчетаване. Оказва се, че това съчетаване е възможно, в резултат на което тук ще изложим теоретичната основа на този нов алгоритъм.

Разглеждаме полиномния вид на двоичен множител Y в n-битова разрядна мрежа с дясно фиксирана запетая:

Умножението на два разряда едновременно означава, че се търси полиномна сума със стъпка два (2) порядъка, т.е. търси се подходящо преобразуване на горния израз, в който елементите на полиномната сума да бъдат през два порядъка. След тази бележка естествено е да забележим как в горния израз всички четни и всички нечетни порядъци се редуват точно със стъпка 2. Излиза, че за да получим исканата полиномна сума търсим преобразование, чрез което всички елементи с нечетни (или четни) порядъци да се преобразуват в изрази с четни (нечетни) порядъци. Ще отбележим като подсказка за следващото изложение, че тук в тази книга, както и най-често на практика, дължината на разрядната мрежа n се приема за четно число. Това означава, че числото (n-1) е нечетно. Последният факт може да се възприеме като едно предварително ограничение.

Нека разгледаме произволна нечетна позиция с номер k, чийто елемент от (3.2.5.5.1) има вида

Ако към този елемент прибавим и после извадим същия елемент, върху получения израз можем да извършим следните преобразования:

От получения краен израз се вижда, че всеки елемент с нечетен порядък може да се представи като разлика от два нови елемента, чиито порядъци са четни. Не е необходимо да доказваме, че ако k е нечетно, то (k+1) и (k-1) са четни числа. Следователно, ако всички елементи с нечетни порядъци се представят по начина (3.2.5.5.2), то в първоначалния полином ще се срещат само четни порядъци, което ще даде възможност полиномната сума да бъде изразена със стъпка 2.

Прилагайки казаното за изходния полином ще получим следното:

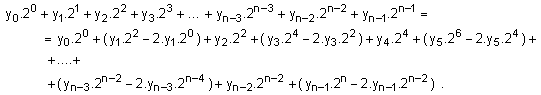
След отваряне на скобите групираме елементите с еднакви порядъци.

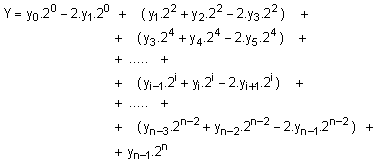
За да получим обща формула за новата елементна сума, се налага да въведем в полинома и позицията с номер (-1), чието съдържание (за да не се променя стойността на множителя) определяме принудително като нула, т.е. (y_-1=0). Така в горния израз за сумата, към двата елемента за позиция с порядък 0, без изменения можем да добавим и елемента (y_-1.2⁰), с което не променяме стойността на множителя. В резултат можем да подредим полиномната сума до вида:

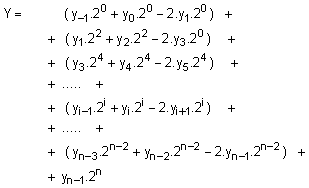
В резултат на този израз по индукция можем да запишем следния нов общ вид на полиномната сума:

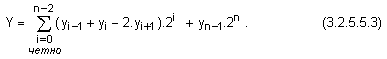
Ако приемем, че изразеното число е представено в допълнителен код, то най-старшата цифра е знаковата цифра. Ако си припомним, че модулът на този код е числото (2ⁿ) (вижте (1.6.2.7)), тогава става ясно, че последният елемент в горната сума (y_n-1.2ⁿ) е число, което е или равно на нула, или е равно на модула на разрядната мрежа. Според определението за допълнителен код, това число, чието тегло е равно на теглото на преноса от най-старшия разряд на разрядната мрежа, не следва да се отчита при определяне на стойността на множителя. Следователно съдържанието на разрядната мрежа може да се изрази окончателно със следната сума:

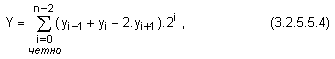
Сега вече операция умножение може да бъде изразена по следния начин:

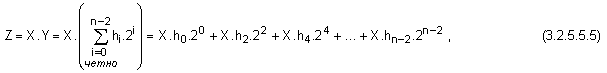
където с h_i е означена сумата

Последното, което остана да се изясни, е какви ще бъдат операциите, назначавани на всеки такт според този алгоритъм. Тези операции зависят от формулата на поразрядния множител h_i, в която участват 3 последователни цифри от двоичния множител Y. Не бива да забравяме, че при определяне на резултантните операции, следва да правим интерпретацията в смисъла на алгоритъма на Бут. Окончателно, за всеки от 8-те случая, резултантните операции са представени в следващата таблица.

Таблица 3.2.5.6.1 Определяне на операцията

yi+1	yi	yi-1	hi = yi-1 + yi - 2. yi+1	операция	коментар
0	0	0	0	+0	среда на група от нули
0	0	1	1	+X	край на група от единици
0	1	0	1	+X	група от една единица
0	1	1	2	+2X	край на група от единици
1	0	0	-2	-2X	начало на група от единици
1	0	1	-1	-X	група от една единица
1	1	0	-1	-X	начало на група от единици
1	1	1	0	+0	среда на група от единици

Алгоритъмът на Мак’Сорли, заедно с дървовидната структура на Уолъс, са едни от най-конкурентните алгоритми при схемната реализация на умножителите.

Още по-висока скорост на умножение може да се получи при паралелна реализация на този алгоритъм. В този случай се формират едновременно (паралелно) всички поразрядни произведения (от всички последователни тройки разряди в множителя), след което в матрицата от суматори се получават междинните суми и крайният резултат. В тази матрица от суматори пък може да се приложи дървовидна структура. Така могат да се съчетаят достойнствата на няколко подхода. По подобен начин са реализирани схемните умножители в съвременните аритметични процесори за работа с фиксирана и с плаваща запетая. За такива разработки за първи път се съобщава през 1982 година.

В някои свръх големи интегрални схеми се прилага вътрешна за схемата бройна система. Като такава е известно да се прилага троична бройна система с цифри {-1,0,1}. Такива системи се наричат системи с излишък по отношение на двоичната бройна система. Излишъкът води до нееднозначно представяне на числата, което се използува по подходящ начин, за да се елиминира възникването на преноси, които от своя страна са основната причина за снижаване на бързодействието на операция събиране.

Следващият раздел е:

3.2.5.6 Умножение с четири разряда едновременно (с младшите разряди напред)

( Multiplication with four bits at the same time (with the juniors ahead) )