3.2.5.6
Умножение с
четири
разряда
едновременно
(с младшите
разряди
напред)
Multiplication with four bits at the same time (with the
juniors ahead)
До
идеята за
умножение с
повече от
един разряд
от множителя
едновременно
се стига твърде
лесно. Интерпретирайки
групата от
цифри на
множителя като
цяло число, с
което трябва
да се формира
всяко
поразрядно
произведение,
се предполага,
че броят на
тактовете,
необходими
за получаване
на
произведението,
ще намалее няколкократно
(пропорционално
на дължината
на групата) в
сравнение с
тези при
последователно
умножение с
цифра по
цифра. В този
смисъл
предварително
е ясно, че
такова
умножение ще
повиши значително
бързодействието
на
операцията. Тъй
като това
повишение е
отнапред
гарантирано,
т.е. то е
абсолютно,
алгоритмите
за умножение
с два и
повече
разряда
едновременно
се отнасят
към групата
на апаратните
методи за
ускоряване
на операция
умножение.
Тук ще
бъде
разгледан
алгоритъм,
който се основава
на метода за
умножение с
младшите разряди
напред по
схемата с
неподвижно
множимо. За
формиране на
поразрядните
произведения
ще бъдат
анализирани едновременно
четири
цифри на
множителя - yi+3 , yi+2 , yi+1 и yi. Може да
се каже, че
това
умножение е
умножение в
16-чна бройна
система, като
се има предвид,
че групата от
4 последователни
бита може да
се разглежда
като тетрада
Н, т.е. като
двоичен код
на 16-чна цифра
(Н=0, 1, 2, 3, ... , E, F).
Подходът към
това
умножение е
аналогичен с
разгледаното
в
предходните
раздели умножение
с 2 разряда
едновременно.
Започваме
с анализ на
възможните
поразрядни
произведения,
които са 16 на
брой (от X.0 до X.F). Поразрядните
произведения
следва да се
събират с
натрупаната
до момента
междинна сума.
Новополучената
сума трябва
да се измести
надясно на 4
бита
едновременно,
което се
налага от избраната
схема за
организация
на умножението,
спомената
по-горе.
Тъй като поразрядните произведения в случая са много и са силно различаващи се по стойност, възниква въпросът как ще бъдат получавани, след като във входния регистър на устройството за умножение ще се съхранява само множимото Х. Неизбежно е да не си припомним подходите за получаване на поразрядните произведения при умножение с 2 разряда едновременно, където чрез логическо изместване наляво лесно се получаваше стойността (2.Х) или (-2.Х). Що се отнася до поразрядните произведения на множимото с нечетната цифри на множителя (3), тя се декомпозираше на сума от възможни цифри, при което се налагаше изпълнение на тези суми в различни тактове. Така например стойността 3.Х се заместваше с израза (-1.Х+4.Х).
Идеята за
подходящото
декомпозиране
на текущата
цифра на
множителя
(имаме
предвид 16-чната
цифра, т.е.
стойността
на цяла
тетрада) явно
се налага да
бъде
приложена и
за настоящия
алгоритъм.
Тук обаче, за
ускоряване на
изчислението
на
поразрядното
произведение,
е удобно да
бъдат
въведени допълнителни
регистри, в
които до края
на умножението,
заедно с
множимото Х,
да се съхраняват
и неговите
декомпозиционни
елементи,
които ще
следва да
бъдат
изчислявани
предварително
преди
началото на
същинското умножение.
Казаното
токущо
следва да
бъде пояснено
по-подробно.
Ще
разгледаме
първоначално
поразрядните
произведения
с цифрите от 0
до 7. Удобните
за
реализация
декомпозиции
са свдени в
следващата
таблица
Таблица
3.2.5.6.1
Поразрядни
произведения
с цифри от 0 до 7
|
Тетрада
yi+3,yi+2,yi+1,yi |
16-чна
цифра |
Поразрядно
произведение |
Не
генерира
корекция в
следващия
такт |
|
0000 |
0 |
X.0=0 |
0 |
|
0001 |
1 |
1X |
0 |
|
0010 |
2 |
2X |
0 |
|
0011 |
3 |
3X |
0 |
|
0100 |
4 |
4X
= X+3X |
0 |
|
0101 |
5 |
5X = 2X+3X |
0 |
|
0110 |
6 |
6X |
0 |
|
0111 |
7 |
7X = X+6X |
0 |
Както
може да се забележи
за лесно и
бързо
получаване
на поразрядните
произведения
в горните
случаи е
удобно да се
разполага в
отделен
регистър
единствено с
числото 3.Х.
Числото 2.Х ще
се получава
от множимото
Х чрез
изместване
на един бит
наляво. За
числата 4.Х, 5.Х,
6.Х и 7.Х ще е
необходим
отделен
суматор. Тази
част на
структурата,
отговорна за
получаване
на тази
разновидност
от
поразрядни
произведения,
може да има
вида, показан
на фигура 3.2.5.6.1.
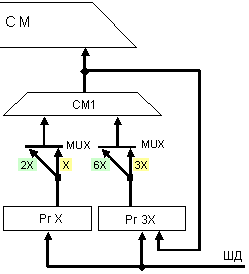
Фиг.
3.2.5.6.1.
Логическа
структура за
формиране на
първите 8
поразрядни
произведения
Първоначално
множимото Х
се зарежда и
в двата
входни
регистъра.
Суматор СМ1
събира изместеното
множимо (2.Х),
подадено по
левия вход от
левия
регистър, с
множимото Х,
подадено от
десния
регистър.
Сумата (3.Х) се
записва чрез
обратната
връзка в
десния регистър.
Така в
последствие,
чрез
подходящото
управление
на връзките,
суматор СМ1
може да
изчислява
всички
поразрядни
произведения
като суми
според
таблица 3.2.5.6.1, в
резултат на
което всички
възможни
междинни суми
се получават
точно.
След
текущото
натрупване
следва
изместване
на
междинната
сума на 4 бита
надясно. Това
се прави и с
множителя, в
резултат на
което се
изхвърля
вече
консумираната
младша цифра
(тетрада).
Ако
следващата
цифра от
множителя е
от първата
половина на
таблицата, тя
се обработва
както вече
беше
пояснено. Но
ако тя е от
втората
половина,
действията
трябва да
бъдат други.
Така
например, ако
текущата
цифра е 8 следва
да се формира
поразрядното
произведение
8.Х. Неговото
получаване
обаче
усложнява
апаратната
реализация,
ако се вземе
решение за
изместване
на 3 бита, тъй
като 8=23. В
същото време
е възможна
декомпозицията
8=16-8=1.24-8. Тези две
операции ще
бъдат
извършени в
следната
последователност
– в текущия
такт ще бъде
изпълнена
операция
изваждане (-8.Х).
При това в
междинната
сума ще възникне
недостиг от
16.Х. Като се има
предвид обаче
предстоящото
4-битово
изместване
надясно, този
недостиг
може да се
добави като
корекция към
междинната
сума с тегло
1.Х. Тук читателят
може да
открие пълна
аналогия с
типа на
корекцията,
която беше
формулирана
в алгоритъма
за умножение
с 2 разряда
едновременно.
В резултат на
това следва да
обобщим, че
за всички
останали
цифри 9, A, B, C, D, E и F ще
трябва да се
приложат
декомпозициите
(16-9), (16-A), (16-B), (16-C), (16-D), (16-E) и (16-F). При това
ще се
изпълняват
резултатните
операции,
преставени
по-нагледно в
следващата
таблица.
Таблица
3.2.5.6.2
Поразрядни
произведения
с цифри от 8 до F
|
Тетрада
yi+3,yi+2yi+1,yi |
16-чна
цифра |
Поразрядно
произведение |
Генарира
корекция +Х в
следващия
такт |
|
1000 |
8 |
-8X
= -2.Х-6.Х |
1 |
|
1001 |
9 |
-7Х =
-Х-6.Х |
1 |
|
1010 |
A |
-6Х =
-6.Х |
1 |
|
1011 |
B |
-5Х =
-2.Х-3.Х |
1 |
|
1100 |
C |
-4Х =
-Х-3.Х |
1 |
|
1101 |
D |
-3Х =
-3.Х |
1 |
|
1110 |
E |
-2Х =
-2.Х |
1 |
|
1111 |
F |
-1Х = -Х |
1 |
Както се вижда от таблицата, в различни случаи се налага изпълнение на операция изваждане както на множимото, така и на неговите декомпозиционни елементи. Така броят на възможните елементи, от които се получава поразрядното произведение, нараства двойно. В резултат на това се усложнява и апаратната реализация, което налага изменения в структурата от фигура 3.2.5.6.1. Измененията в структурата са представени на фигура 3.2.5.6.2.
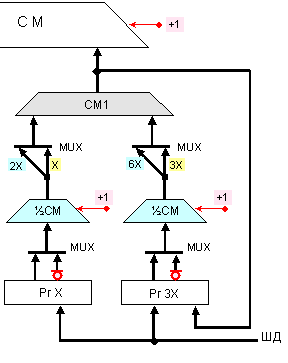
Фиг.
3.2.5.6.2
Логическа
структура за
формиране на
поразрядните
произведения
Операция изваждане се изпълнява с използване на допълнителен код на операндите, за което са използвани инверсните изходи на тригерите в регистрите РгХ и Рг3Х, при това в някои случаи едновременно. Този код налага включването на полусуматорите ½СМ.
Възможността
текущата тетрада
да генерира
корекция (+Х),
която следва
да се отчете
в следващия
такт, налага
всяко текущо
умножение да
се разгледа и
в условията
на
възможната
корекция.
Признак за това,
че текущият
такт трябва
да отчете не
само
текущата
цифра на
множителя, но
и вероятната
корекция (+Х) от
предидущия
такт, се
сигнализира
от логическа
функция,
която ще
означим K(t).
Таблицата,
която
обобщава
всички
възможни
случаи,
когато в
текущия такт
се налага да
се отчита
корекцията, е
представена
по-долу.
Таблица
3.2.5.6.3 Поразрядни
произведения
с цифри от 0 до F,
при
необходимост
от корекция
|
|
16-чна
цифра |
Поразрядно
произведение |
|
|
1 |
0 |
+X |
0 |
|
1 |
1 |
+2X |
0 |
|
1 |
2 |
+3X |
0 |
|
1 |
3 |
+Х +3X |
0 |
|
1 |
4 |
+2X +3X |
0 |
|
1 |
5 |
+6X |
0 |
|
1 |
6 |
+Х +6X |
0 |
|
1 |
7 |
+2X +6X |
0 |
|
1 |
8 |
-Х -6Х |
1 |
|
1 |
9 |
-6Х |
1 |
|
1 |
A |
-2Х -3Х |
1 |
|
1 |
B |
-Х -3Х |
1 |
|
1 |
C |
-3Х |
1 |
|
1 |
D |
-2Х |
1 |
|
1 |
E |
-Х |
1 |
|
1 |
F |
+0 |
1 |
В случаите, когато в текущия такт липсва корекция, т.е. K(t)=0, действията се определят според таблици 1 и 2. Тъй като корекция генерират само цифрите по-големи от 7, уравнението на логическата функция K(t) е следното:
![]()
С други
думи признак
за корекция е
старшият бит
на текущата
тетрада. От
това следва
изводът, че
след
изместване
надясно на
множителя,
този бит не
следва да се
загубва, което
налага
регистърът
на множителя
Y да
съдържа един
допълнителен
тригер отдясно.
Този тригер
може да бъде
причина за
една
допълнителна
операция
събиране (+Х),
ако в последния
такт в него
се окаже “1”.
И накрая
трябва да
отбележим, че
конструкторът
следва да
съобрази
дължините на
отделните
елементи и на
получаваните
суми в
структурата от
фигура 3.2.5.6.2,
които се
удължават
отдясно по причина
на
изместванията
с един или с
два бита, а
още и от
възможните
преноси при
събиране. А
суматор СМ1
трябва да
подава към
изходния
суматор СМ
събираемо в
пълен формат.
Тези
забележки
следва да
определят
крайния
формат на
всеки
логически
възел в
структурата,
както отляво,
така и
отдясно на
основния
формат на
операндите.
Пълната
логическа
структура на
устройство
за умножение
с 4 бита
едновременно,
както и
съответната
за нея
микропрограма,
оставяме
като задача
за
самостоятелна
работа на
читателя. Вариант
на
алгоритъма
за умножение
в допълнителен
код тук не
представяме.
Такъв читателят
може лесно да
синтезира,
като търси аналог
с алгоритъма
за умножение
на 2 разряда едновременно.
Представените
в предидущите
пунктове
решения
могат да
бъдат пример
за търсеното
тук решение.
Илюстрация
на алгоритъма
чрез
подходящи
числени примери
читателят
може да
намери в книга [2].
Следващият
раздел е:
3.2.5.7 Схемни
умножители ( Hard multiplier )