3.2.5.7 Схемни умножители

Hard multiplier

Съществуват още много други подходи за ускоряване на операция умножение. Така например, в случаите, когато за представяне на числата се използва 16-тична бройна система, се предлагат алгоритми за умножение на 4 двоични разряда едновременно (4 двоични разряда представят една 16-тична цифра). Това по същество е умножение в шестнадесетична бройна система и отнапред ясно, че то ще се изпълнява 4 пъти по-бързо в сравнение с последователното умножение бит по бит. Принципно обаче умножението с 4 разряда едновременно не се отличава от това с 2 разряда едновременно, което вече изложихме, ето защо тези алгоритми ние не представяме тук.

Удобен за реализация е и един друг алгоритъм, в който се натрупват паралелно, т.е. едновременно, две междинни суми. Това ускоряване на операция умножение се основава на формално “разсичане” на множителя на две части, при което дължината на подмножителите се скъсява двойно. Подмножителите представляват старшата и младшата половина на разсечения множител. Така умножението се извършва според израза:

От горната формула се вижда възможността за паралелно във времето изпълнение на две операции умножение с последващо подходящо събиране на получените полупроизведения. Не е трудно да се съобрази, че умножение по тази алгоритмична схема ще се изпълнява почти 2 пъти по-бързо в сравнение с последователното умножение бит по бит.

Изложените подробно до момента алгоритми за умножение, както и споменатите по-горe, се характеризират с това, че в логическите структури на устройствата, които ги реализират, е включен само един суматор. Това означава, че циклическото натрупване, произтичащо от записа (3.2.2.1), се организира върху този единствен суматор последователно във времето, дискретизирано от управляващото устройство.

Тъй като нашето изложение по принцип е подчинено на разглеждането на решенията в светлината на последователното повишаване на тяхното качество, тук по-долу ще се спрем на подходи, целящи по-нататъшно радикално решаване на проблема с бързодействието на операция умножение.

Кардиналното решение на задачата за повишаване на бързодействието на операция умножение се основава на идеята за построяване на логическа структура с много суматори, естествено комбинационни. При такава реализация на съответните алгоритми се очаква превръщане на цялостното решение в комбинационна схема, т.е. свеждане на операцията до еднотактна. Разработването на това решение се основава на изразяване на умножението по следния начин:

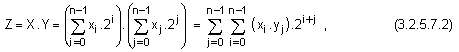
където се имат предвид n-разрядни числа без знак.

Според този начин на изразяване на произведението, последното може да бъде получено от поцифрените двоични произведения (x_i*y_i), подходящо разместени и събрани. Така например умножението на две 4-разрядни двоични числа може да се изрази по метода с младшите разряди напред чрез следната схема:

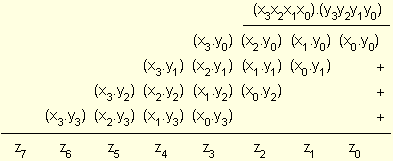
В представената схема произведението се натрупва от 4-те поразрядни произведения, които са записани като наредени (конкатенирани) последователности от поцифрените произведения с поредната цифра на множителя. Този запис не противоречи на правилата на позиционните бройни системи, каквато в случая е двоичната. Така при двоични числа непосредствената реализация на тази схема изисква дву-входови логически елементи “И” за получаване на поцифрените произведения. Читателят лесно може да се убеди, че поцифреното произведение в двоична бройна система се дефинира с таблица, която е еквивалентна на таблицата на истинност на елементарната логическа функция “конюнкция”. Можем да интерпретираме поразрядното произведение и по следния начин:

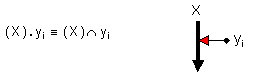
Фиг. 3.2.5.7.1. Структурна реализация на двоичното поразрядно произведение

Както е показано на фигура 3.2.5.7.1, при двоични числа i-тото поразрядно произведение има естествено структурно и логическо изражение.

Както вече споменахме, еднотактното натрупване на така формираните поразрядни произведения налага последователно подреждане с изместване един спрямо друг на (n-1) на брой двоични n-разрядни комбинационни суматори.

В резултат на изложените разсъждения, за примера по-горе се получава логическата структура на умножител, показана на фигура 3.2.5.7.2, наречена матрична.

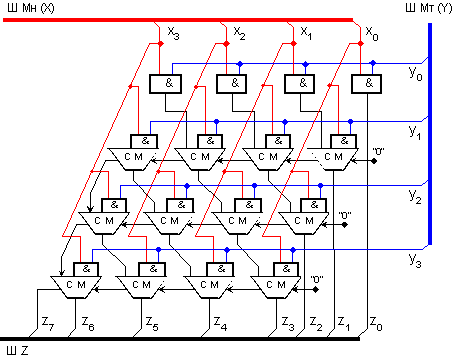
Фиг 3.2.5.7.2. Логическа структура на схемен умножител

с хоризонтално разпространяващи се преноси

Изпълнението на умножаващата матрица от фигура 3.2.5.7.2 реализира умножение на числа без знак (по модул). Максималното време за превключване на такава схема може да се оцени като сума от времето за разпространение на преноса в първия ред суматори, плюс времето за събиране по вертикала и плюс времето за разпространение на преноса в последния ред суматори:

където t_p и t_z представляват съответно времената за формиране на преноса и на сумата в едноразрядните суматори.

Основен проблем при синтеза на схемните умножители е минимизирането на времето за превключване на умножаващата матрица. Подходите за оптимизация в този смисъл са два:

- намаляване дължината на веригите от хоризонтално разпространяващи се преноси ;

- намаляване броя на вертикално натрупващите се суми.

Прилагането на първия подход води до получаване на два вида умножаващи матрици:

- матрица "с диагонални преноси" ;

- матрица "с прескачане на ред" .

Умножаващата матрица с диагонални преноси се получава когато преносите се подават не към хоризонтално разположените едноразрядни суматори, а изпреварващо в колонките, към суматорите в следващото ниво на матрицата. На фигура 3.2.5.7.3 казаното е илюстрирано чрез един централен фрагмент от принципната схема на матрицата.

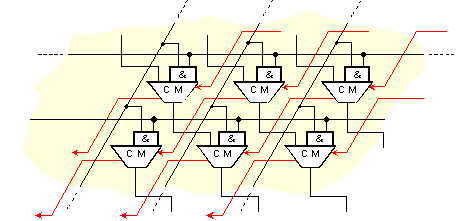
Фиг. 3.2.5.7.3. Централен фрагмент от схема с диагонални преноси

В матричната схема с диагонални преноси времето за умножение се оценява както следва:

Идеята за изпреварващото по вертикала подаване на преноса може да се приложи и по отношение на сумата. В резултат на това се получава така нареченото събиране с прескачане на ред. По-долу на фигура 3.2.5.7.4, е показана принципната схема на умножаваща матрица с размери 5х5 бита, в която освен идеята за диагонални преноси, е реализирана и идеята за изпреварващо подаване през ред и на сумата.

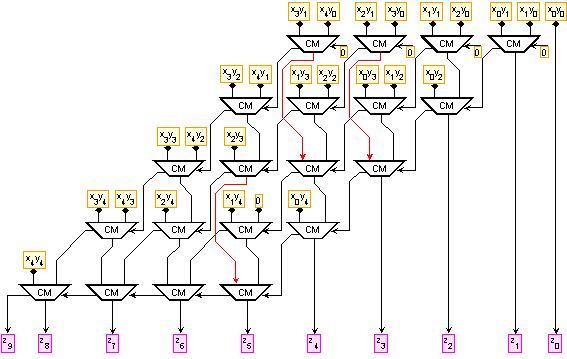
Фиг. 3.2.5.7.4. Принципна схема с прескачане на ред

Събирането с прескачане на ред позволява да се изравнят закъсненията във веригите на преноса със закъсненията в сумиращите вериги. Както се вижда от примера, дължината на суматорите на всички нива е намалена на (n-1) разряда. В резултат времето за превключване на матрицата в общия случай се оценява както следва:

Получената оценка показва, че с прилагане на по-горе изяснените подходи за оптимизация на принципната схема на умножаващата матрица, може да се постигне високо бързодействие. За съжаление подходът с прескачане на ред прави схемата на матрицата от суматори с твърде нерегулярни връзки, които зависят от конкретната разрядност на операндите. Както може да се види от представения на фигура 3.2.5.7.4 пример такова изпреварващо подаване на сумата е осъществено само за три от суматорите.

По-нататъшното ускоряване на умножаващата матрица може да се постигне чрез използуване на суматори с паралелен пренос, но те от своя страна внасят допълнителна нерегулярност. Суматор с паралелен пренос е най-целесъобразно да се използува в най-долния ред в схемата с диагонални преноси, т.е. на изхода, при окончателното получаване на произведението.

Вторият подход води до дървовидно свързване на двоичните суматори. При този подход се извършва иерархично редуциране на междинните суми до две числа, които се събират в един изходен суматор с паралелен пренос. Целта естествено е минимизиране на броя на суматорите във вертикално направление.

Същността на процеса на построяване на дървото се състои в следното: подредените поцифрени произведения (x_i*y_i) се разглеждат не хоризонтално (в качеството им на поразрядни произведения), а вертикално, като множества от цифри с едно и също тегло, теглото на съответната колонка (позиция в произведението). На събиране в едноразряден суматор се подлагат две или три цифри (суми и преноси) с едно и също тегло, т.е. цифри от една и съща колонка. След първия етап на групиране на цифрите за събиране в колонки, максималната дължина на колонките се редуцира до 2/3. На следващият етап се групират отново по две или три цифри (суми и преноси от съседни колонки) за събиране в едноразряден суматор. Така процесът на групиране продължава, докато във всяка колонка останат само две (една) цифри. Броят на нивата, необходими за редуциране на междинните суми до два операнда се оценява с израза:

Този израз оценява и времето за превключване на умножителя, тъй като по същество то представлява последователна (по вертикала) сума от времената за превключване на отделните нива на дървото. Времето за превключване на умножителя е пропорционално на N и е значително по-малко в схемите с матрично свързани суматори, особено за големи дължини на разрядната мрежа.

Процесът на групиране е неформален, което означава, че не може да се очаква получаването на регулярна структура за умножаващата матрица. С други думи, структурата на умножаващата матрица е нерегулярна и следва да се синтезира изцяло и отново за всяка нова дължина на разрядната мрежа. По-долу процесът на групиране е илюстриран за разрядна мрежа с дължина n=5[b]. При умножаване на две 5 разрядни числа, поцифрените произведения, които представляват двоични цифри, се подреждат по следния начин:

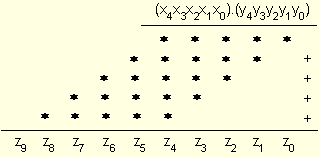
при което формират девет колонки, номерирани от 0 до 8. Най-старшата позиция с №9 се формира от стойността на преноса. Тъй като операция събиране по съществo следва да бъде изпълнена върху вертикално разположените цифри, схемата може да се подреди и по следния начин:

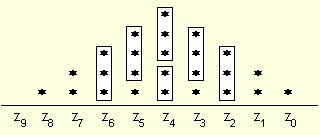
В горната схема е извършено посоченото вертикално групиране на двоични цифри (стойности на поцифрените произведения, означени със звезди), които могат да се подадат за събиране в един едноразряден суматор. Петте пълни едноразрядни суматора формират първото ниво в дървовидната структура на умножаващата матрица, която синтезираме в момента. Всеки суматор има два изхода – за получените сума S1 и пренос p1, които разпространява за натрупване в съответствие с позиционното тегло на колонките, както е показано в следващата схема:

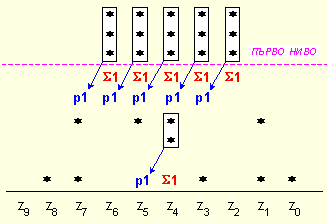
След подреждане на суматорите от първото ниво, както и на получаваните от тях суми и преноси към останалите несъбрани още цифри, се извършва следващото групиране. Спазва се същия принцип, при което се формира второто ниво от суматори - заградените групи от цифри показани на следващата схема:

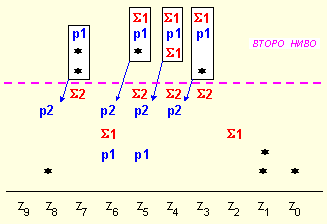
Сумите S2 и преносите p2 от второто ново суматори се подреждат съответно заедно с неучаствалите в събирането поцифрени произведения. В някои позиции продължават да се получават по няколко цифри за събиране – несъбрани още суми и преноси от първо ниво, от второ ниво, както и поцифрени произведения. Върху тези цифри се извършва следващото групиране за третото ниво:

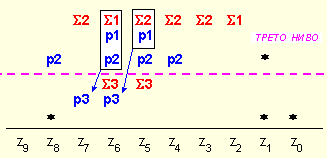
Може да бъде забелязано, че групирането в трето ниво е направено така, че в последния ред да има суматори поне за по две цифри. Така на изхода за събиране се подреждат следните два операнда:

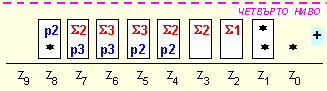
съставени от цифри на суми и преноси от първо, второ и трето ниво на дървото от двоични суматори както и от невключени до момента цифри на поцифрени произведения. Тези два операнда се събират в изходен суматор с паралелен пренос.

Окончателната логическа структура на дървовидния умножител с размери 5х5, който току що синтезирахме, е представена на фигура 3.2.5.7.5.

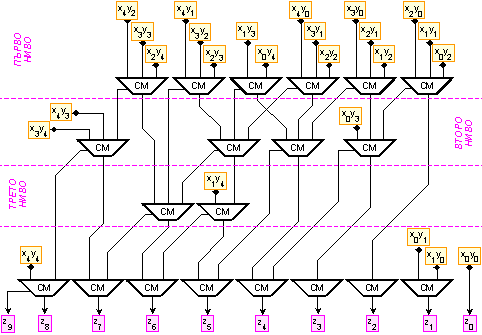
Фиг. 3.2.5.7.5. Принципна логическа схема на дървовиден умножител 5х5

Както може да се види от горната схема, едноразрядните двоични суматори са свързани във вертикално направление (отгоре надолу) в своеобразна дървовидна схема. Тази дървовидна схема е известна под наименованието “дърво на Уолъс (Wallace)”.

За реализация на схемните умножители се прилагат различни алгоритми. Най-често умножаващата матрица работи както върху числа без знак, така и върху числа със знак, представени в допълнителен код. С цел да се получи еднородност в схемата на умножаващата матрица, най-често се прилага алгоритъмът на Бут.

Следващият раздел е:

3.2.6 Операция деление ( Division )