3.2.7 Други методи за деление

Other methods for division

Съществуват множество реални примери, в които операция деление се изпълнява чрез операция умножение. Идеята се състои в замяната на непосредственото деление X/Y с израза X.(1/Y), в който делимото Х се превръща в множимо, а от делителят Y сравнително бързо може да се получи реципрочната стойност 1/Y. Следва да се обърне внимание на факта, че реципрочната стойност е число по-малко от единица, т.е. най-удобна за неговото представяне е формата с ляво фиксирана запетая.

За изчисляване на реципрочната стойност се прилагат различни итерационни сходящи числени методи. Тук ще бъде представен такъв, основаващ се на разложението на функцията

в сходящ степенен ред. Аргументът e на тази функция представлява безкрайно малко число. Основанията за този избор на функция се налагат при следните разсъждения: ако се приеме например, че числото A_k е известно k-то приближение на реципрочната стойност на делителя Y, то относителната погрешност e_k, с която приближението представя истинската стойност, може да бъде оценена така:

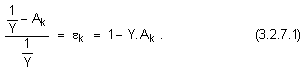
И така, ако е известно някакво приближение A_k, то е известна и относителната погрешност e_k, а тогава горният израз може да послужи за изразяване на търсената величина:

Тъй като e_k<1 по условие, то дробта (отношението)

може да се разложи в безкраен сходящ степенен ред:

В зависимост от това каква скорост на сходимост на алгоритъма желаем да постигнем, избираме броя на елементите от реда, с които ще заместим разложената величина. Обикновено се работи само с един или два елемента от реда, т.е.

Ако се замести отношението 1/(1-e_k) в уравнение (3.2.7.2) например с първата от тези формули, включваща само два елемента от степенния ред, то тогава равенството в това определение се нарушава и тъй като отношението е заместено с едно първо приближение, може да се приеме, че така се определя само следващото приближение към истинската стойност на реципрочността, т.е.

За да може да се използва полученото като рекурентна формула за изчисляване на всяко следващо приближение, е необходима формула за изчисляване на текущата погрешност e_k. Такава може да се получи от уравнение (3.2.7.2):

След заместване се получава окончателния вид на рекурентната формула за новото приближение към търсената реципрочна стойност:

Когато за относителната погрешност e_k е избрано приближението с три елемента от степенния ред, рекурентната формула за изчисляване на следващото приближение, е следната:

Прилагането на първата формула (3.2.7.4) е по-изгодно, тъй като с умножението Y.A_k се получава и разликата (2-Y.A_k), която може да се разглежда като допълнителен код на умалителя (-Y.A_k). С други думи реализацията на рекурентната формула (3.2.7.5) изисква две операции умножение.

За да започне итерационният процес за изчисление на реципрочната стойност е необходимо да се избере началното приближение A₀, при това така, че относителната погрешност e да удовлетворява условието за сходимост, т.е. e<1. Тъй като оценката за приемливата относителна погрешност e е известна предварително (тя се определя от възможностите на разрядната мрежа), то като за начало неравенството може да се запише така:

откъдето се прави изводът, че 0 < Y.A_k < 2 , което се отнася и за k=0, т.е.

При условие, че делителят Y е ляво нормализирано положително число в една n-битова разрядна мрежа, то е изпълнено неравенството (3.2.6.3). Тогава горното условие за избор на начално приближение се определя окончателно така:

И така, на ляво нормализиран делител Y=(0 1yy…yyy) в n-битова разрядна мрежа с дясно фиксирана запетая:

съответства начално приближение

което ще бъде представено в разрядна мрежа с ляво фиксирана запетая:

което според неравенство (3.2.7.8) може да бъде избрано измежду следните n-разрядни стойности:

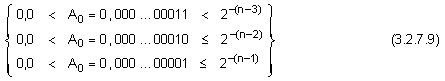
Заедно с изчисляването на приближенията A₁ , A₂ , A₃ , ... , A_k трябва да се изчисляват и съответните им относителни погрешности e₁ , e₂ , e₃ , ... , e_k, които гарантирано намаляват и клонят към нула. Навярно на читателя вече е ясно, че условието за край на цикличното итерационно изчисление на реципрочната стойност се формулира чрез относителната погрешност с помощта на следното неравенство:

Като се има предвид, че при умножение броят на цифрите на произведението е два пъти по-голям, това означава, че броят на верните цифри във всяко следващо приближение, изчислявано по формулата (3.2.7.4), ще се удвоява. Ако се избере начална стойност A₀, в която има две верни значещи цифри, например 000...0011, това означава, че за представяне на реципрочната стойност в поле с 32 верни цифри, ще са необходими четири итерации (k=4) или 8 умножения (по 2 на итерация, виж (3.2.7.4)). Като се прибави и последното умножение X.A_k, времето за деление по този начин може да се оцени на 9 умножения. В процесори, в които операция деление не е изпълнима операция, изложеният по-горе метод за деление позволява значително по-бърза реализация, отколкото програмно моделиране на непосредственото деление под формата на специализирана подпрограма.

Подробен синтез на алгоритъм за деление, на логическа структура на устройство за деление, на микропрограма, както и множество числени примери, читателят може да намери в книга [3].

Следващият раздел е:

3.2.8 Деление на числа в допълнителен код ( Division two’s complement numbers )