3.2.9.1
Метод на
малките
остатъци
Small Residue Method
Идеята
на метода се
състои в
намиране на
признак, с
помощта на
който да може
да бъде предсказана
следващата
цифра на
частното и да
бъдат
спестени
предстоящите
микрооперации
изместване и
събиране (изваждане).
Това желание
изисква
подробен анализ
на всеки
текущ
частичен
остатък Rm.
Необходимо е
да бъдат
разгледани
два случая в
условията на
деление по
модул:
а)
Случай на
положителен
частичен остатък - Rm , Rm>0 .
Когато
остатъкът
изпълнява
това условие,
поредната
цифра на
частното е
единица: zm=1. Според
алгоритъма
за деление
без възстановяване
на остатъка,
следващите
микрооперации
са
изместване
наляво
(когато
схемата за
деление е
организирана
с неподвижен
делител) и
изваждане.
Тези
две микрооперации
обаче се
разглеждат
при едно
допълнително
условие -
полученият
частичен
остатък да е твърде
"малък", в
сравнение с
нормализирания
делител. Ще припомним,
че
нормализираният
делител има вида
W=01www…w. Това
допълнително
условие
означава, че
остатъкът Rm е твърде
силно
ненормализиран
по отношение
на делителя.
Тази
ситуация
практически може
да бъде
разпозната
по наличието
на група от незначещи
цифри,
непосредствено
вдясно от
знаковия
разряд, а когато
остатъкът е
положително
число, тези
цифри са
нули. Нека
приемем в
общия случай,
че дължината
на тази група
е r на брой бита.
Тогава видът
на остатъка
ще бъде следния:
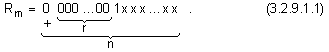
Такъв
остатък се
нарича малък.
В
този случай,
според
определението
(3.2.6.14), за изчисляване
на следващия
частичен
остатък Rm+1,
трябва да се
изпълнят
микрооперациите
изместване
наляво и
изваждане:
![]()
За
този остатък
може да се
твърди и без
да се
извършват
означените
за неговото
получаване
операции, че
е
отрицателен: Rm+1<0 !
В
това сме
напълно
сигурни, като
имаме
предвид, че
едно
изместване
наляво
съвсем не е
достатъчно
да
нормализира малкия
остатък (3.2.9.1.1).
Очевидно е,
че след вече
записаната в
частното
цифра zm=1, ще
трябва да се
добави една
нула: zm+1=0.
Тъй
като Rm+1<0, то следващият
частичен остатък
Rm+2 трябва
да се получи
по правилото:
![]()
Ако
обаче
заместим Rm+1 с
неговия
израз, ще
получим
![]()
От
този краен
вид на
частичния
остатък се вижда,
че и двойното
изместване
на остатъка Rm не е в
състояние да
го нормализира
и че без да се
извършват
означените
действия,
отново може
да се твърди,
че и този
остатък ще
бъде
отрицателен,
т.е. Rm+2<0, а с това
и следващата
цифра в
частното е предопределена
да бъде нула: zm+2=0.
Без
да
продължаваме
с подробното
последователно
разписване
може да се
каже, че
всички следващи
частични
остатъци
![]()
ще бъдат
предварително
известни като
отрицателни,
а на тях като
поредни цифри
в частното ще
съответствуват
само нули, т.е.
![]()
Едва
остатъкът Rm+r, имащ вида:
![]()
ще бъде
за нас с отнапред
неизвестен
знак и
следователно
действията,
от които той
се получава,
ще трябва да
бъдат фактически
изпълнени.
Фактическото
изчисление
на остатъка Rm+r е
необходимо
както за
определяне
на съответствуващата
му цифра в
частното,
така и за определяне
на
следващата
аритметична
операция.
В
заключение
ще обобщим,
че при
получаване на
малък
положителен
остатък Rm от вида (3.2.9.1.1),
в частното се
определят
едновременно
r на брой
цифри (100...00)
- една
водеща
единица и
група от (r-1) нули.
Следващият
остатък,
който трябва
да се
изчисли, се
получава
след
изместване
на r разряда
наляво на
частичния
остатък и изваждане
на делителя,
т.е. по
формулата:
![]()
Ако
това
изчисление
трябва да се
извърши
бързо,
изместването
трябва да
стане на r
разряда
едновременно.
Очевидно когато полученият частичен остатък не е малък, делението трябва да се извършва последователно, както вече беше изяснено.
б) Случай
на
отрицателен
частичен остатък - Rm
, Rm<0 .
Отрицателният
остатък също
може да бъде
разгледан
като малък,
ако редът на
неговия полином
след
поредната
операция се е
оказал
значително
по-малък от
този на
нормализирания
делител W. Признак
за това
отново е
групата от
незначещи
цифри вдясно
от знаковия
разряд. Тъй
като
отрицателният
остатък
неизбежно ще
бъде
представен в допълнителен
код, то тези
незначещи
цифри ще
бъдат единици.
Видът на
такъв
частичен
остатък е
следния:
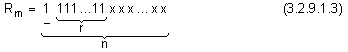
Понеже
остатъкът е
отрицателен,
според правилото
(3.2.6.14), поредната
цифра в
частното е
нула zm=0. Пак по
силата на
същото
правило,
следващата
операция е
събиране:
![]()
Гледайки
определението
(3.2.9.1.3),
аналогично
на предния
случай, можем
без да
извършваме
действията
да твърдим,
че този
частичен
остатък е
гарантирано
положителен.
Както (m+1)-вия
остатък,
както и за
всички
следващи
![]()
може
да се твърди,
че ще бъдат
положителни, без
да е
необходимо
фактическото
им изчисление,
а
съответствуващите
им цифри в
частното ще
бъдат единици.
Едва след
нормализирането
на остатъка,
увереността
в следващата
след знака на
остатъка
цифра
изчезва и той
трябва да
бъде изчислен
фактически,
което става
по формулата:
![]()
В
заключение
ще обобщим,
че при
получаване на
малък
отрицателен
частичен
остатък Rm от вида (3.2.9.1.4),
в частното се
определят
едновременно
r на брой
цифри (011...11) - една
водеща нула и
група от (r-1)
единици. За
определяне
на
следващата (m+r)-та
цифра, е
необходимо
да се изчисли
остатъкът Rm+r по
горната
формула, тъй
като
неговият
знак е
непредсказуем.
Това
изчисление
може да се
извърши в
един такт,
ако се
извърши r-разрядно
изместване
на остатъка Rm.
Тъй
като
дължината на
групата от
незначещи
цифри r е
променлива
величина и
зависи от
конкретните
операнди, то
еднотактното
изместване
на r разряда
е съществен и
актуален
проблем. Той
се решава с
помощта на
така
наречените
програмируеми
изместващи
матрици, на
чиято структура
ще се спрем
по-нататък.
Ако отрицателният остатък не е малък, делението се извършва по силата на вече изложените алгоритми като на всеки такт се определя по една цифра от частното.
И така, можем вече да изкажем кратко алгоритъма за деление, произтичащ от този метод. По същество той съдържа същите три етапа, както и класическия – проверка на условията за дефинираност и за изпълнимост, лява нормализация на операндите и същинско деление. В етапа на същинското деление алгоритъмът е циклически от вида с предварително известен брой повторения – броя на неизвестните цифри на частното. На всеки такт се получава нов частичен остатък, който със своя знак определя текущата цифра в частното. След това, ако в остатъка бъде открита група от r на брой незначещи цифри, в частното се записват още (r-1) цифри, определени от вида на групата. Следва лява нормализация на частичния остатък и изчисляване на следващия остатък.
Ако не се разпознае група от незначещи цифри, се извършва изместване на остатъка на ляво само на един бит и се изчислява следващият частичен остатък.
Така се продължава докато се определят всички неизвестни цифри на частното.
Апаратната
реализация
на този метод
за деление по
същество
може да бъде
реализирана
в базовата
логическа
структура от
фигура 3.2.6.3, но
измененията
в нея ще
бъдат
съществени.
На първо
място трябва
да се изгради
схема за разпознаване
на групата от
незначещи
цифри и определяне
на нейната
дължина r. С
помощта на
параметъра r следва да се
програмират
връзките за
изместване в
регистъра на
частното и в
суматора.
Нещо повече,
трябва да се
промени и
възелът за
контрол на
броя на цифрите
БрЦ, в
който ще
трябва да се
реализира
операцията (БрЦ)-r.
Известен
компромис и
облекчаване
на апаратната
реализация
на метода
може да се
постигне
чрез
фиксиране на
определена
дължина r=const, която да
се наблюдава.
Eстествено,
че в този случай
възможностите
на метода се
снижават
значително, тъй
като всички
групи от
незначещи
цифри с дължина
по-малка или
по-голяма от r ще бъдат
обработвани
последователно.
В заключение трябва да се обърне внимание на вече изяснения характер на метода относно повишаването на бързодействието на операция деление. Това повишаване не е гарантирано, то не е абсолютно и зависи от конкретността на операндите. Следователно то е повишение, което се изявява в статистически смисъл, т.е. колкото повече операции деление се изпълнят по този алгоритъм, толкова по-голяма е вероятността за изява на неговото достойнство и на спестеното време.
Числени
примери,
илюстриращи
тези ускорени
алгоритми,
читателят ще
намери в книга
[2].
Следващият
раздел е:
3.2.9.2
Метод на
големите
остатъци ( Large residue method )