3.2.9.2 Метод на големите остатъци

Large residue method

Алтернативата на малкия остатък естествено е големият остатък, ето защо този случай се анализира отделно. Получаването на "голям" частичен остатък в процеса на деление представлява случай, който формално може да се изрази със следното приблизително равенство (равенство отдолу):

Големият частичен остатък е приблизително равен на нормализирания делител. За съжаление отношението приблизително равно не е достатъчно детерминирано и не може да се провери непосредствено. Налага се да се търсят други идеи.

Идеята, на която се основава методът на големите остатъци, се състои в следното очевидно заключение - ако дясната част на определението (3.2.9.2.1) се прехвърли отляво ще се получи еквивалентното съотношение

то от само себе си навежда на мисли за вече разгледаната основополагаща идея в метода на малките остатъци. Или с други думи, горният израз показва, че големият остатък може да бъде разпознат чрез малката разлика.

Малката разлика (3.2.9.2.2) се нарича приведен остатък . Тя се получава чрез изваждане или събиране на текущия частичен остатък с нормализирания делител. В зависимост от знака на приведеният остатък следва да се разгледат два случая:

а) Случай на положителен частичен остатък - R_m , R_m>0.

В този случай поредната цифра на частното е единица, z_m=1. В същото време приведеният остатък следва да се получава така:

който е малък и отрицателен. Това, че приведеният остатък е такъв може да се разпознае, ако той има вида (3.2.9.1.3)

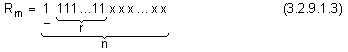
Естествено най-удобно е в този случай да се приложи методът на малките остатъци, т.е. след вече записаната в частното цифра z_m, да се запишат още (r-1) единици

които и без това ще бъдат записани ако се изпълнят последователните микрооперации на класическия алгоритъм, когато големият остатък ще предизвика в следващия такт много малка положителна разлика. Това може да бъде съобразено и без да се извършват фактически тези действия. На това предсказано определяне на цифрите в частното имаме право по силата на предварително известните знаци на следващите (r-1) частични остатъци.

Предварителната увереност за значението на знаците се изчерпва едва при остатъка R_m+r, който следва да бъде изчислен фактически по следния начин:

Според тази формула операцията събиране се предхожда от r-разрядно изместване наляво на приведения остатък, което за да има необходимия ефект, трябва да се изпълни за един такт.

Определените в рамките на този такт цифри в частното са или една (1) или r на брой единици като цяла група (1 11...1), които следва да бъдат отброени от БрЦ .

Ако след получаване на приведения остатък той не отговаря на вида (3.2.9.1.3), делението продължава последователно със следващия по ред остатък :

След получаване на новия остатък R_m+r (или R_m+1), делението отново продължава по описания вече начин - получаване на приведения остатък и запис на новите цифри в частното до определяне на всичките му неизвестни цифри.

б) Случай на отрицателен частичен остатък - R_m , R_m<0.

Когато остатъкът е отрицателен, поредната цифра в частното e нула z_m=0, а приблизителното равенство (3.2.9.2.1) може да се провери чрез свеждане към еквивалентното му по следния начин:

От този израз се получава гарантирано положително число

което е малко число и може да се разпознае, ако има вида (3.2.9.1.1)

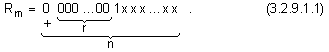
Обработването на така полученият приведен остатък по метода на малките остатъци означава, че в частното, след вече записаната цифра z_m=0, могат да се запишат еднотактно още (r-1) на брой цифри нула

.

Това може да се направи без фактическото изчисляване на съответните остатъци

тъй като тяхното отношение спрямо нулата е предварително известно. Следващият остатък, който наистина трябва да бъде изчислен, е остатък R_m+r, тъй като неговият знак предварително не може да бъде предсказан. Изчислениeтo му се осъществява по следната формула:

от която личи, че изваждането на нормализирания делител W, се предхожда от r-разрядно изместване наляво на приведения остатък

Ако след получаване на приведения остатък според горния израз, не се установи, че той съответствува на вида (3.2.9.1.1), т.е. не се установи че той е малък, то този текущ такт остава само с една определена цифра - z_m=0. След което делението продължава с последователна стъпка към следващия остатък:

Определените в текущия такт цифри в частното са или една (0), или група от r на брой (0 00...0) нули. И в двата случая в края на такта те трябва да се отброят в БрЦ .

Ако приведеният остатък не е малък, делението се извършва по силата на вече изложените алгоритми като на всеки такт се определя по една цифра от частното.

И така, можем вече да изкажем кратко алгоритъма за деление, произтичащ от този метод. По същество той съдържа същите три етапа, както и класическия – проверка на условията за дефинираност и за изпълнимост, лява нормализация на операндите и същинско деление. В етапа на същинското деление алгоритъмът е циклически от вида с предварително известен брой повторения – броя на неизвестните цифри на частното. На всеки такт се получава нов частичен остатък, който със своя знак определя текущата цифра в частното. След това се изчислява приведеният остатък, Ако в него бъде открита група от r на брой незначещи цифри, в частното се записват още (r-1) цифри, определени от вида на групата. Следва лява нормализация на приведения остатък и изчисляване на следващия частичен остатък.

Ако в приведения остатък не се разпознае група от незначещи цифри, се извършва изместване на остатъка на ляво само на един бит и се изчислява следващият частичен остатък.

Така се продължава докато се определят всички неизвестни цифри на частното.

В заключение трябва да се отбележи, че всичко което беше казано за апаратната реализация на метода на малките остатъци, се отнася до голяма степен и за метода на големите остатъци. Много често двата метода се комбинират, тъй като възможностите за това са очевидни.

В заключение трябва да се обърне внимание на вече изяснения характер на метода относно повишаването на бързодействието на операция деление. Това повишаване не е гарантирано, то не е абсолютно и зависи от конкретността на операндите. Следователно то е повишение, което се изявява в статистически смисъл, т.е. колкото повече операции деление се изпълнят по този алгоритъм, толкова по-голяма е вероятността за изява на неговото достойнство и на спестеното време.

Числени примери, илюстриращи тези ускорени алгоритми, читателят ще намери в книга [2].

Следващият раздел е:

3.2.9.3 Схемен делител ( Hard divisor )