3.2.9.4 Схемен
делител. Остатък
Hardware divider. Calculation of the Remainder
Вече посочихме, че операция деление Z=X/Y, като най-сложна, за разлика от всички други, генерира два самостоятелни резултата, изисквани в изчислителните алгоритми. Тези два резултата са частното Z и остатъкът R. Чрез тези два резултата може да бъде дадено следното определение на операция деление: частното и остатъкът са такива числа, щото Z.Y+R=X.
Ще припомним още, че
![]()
при
което Y се нарича модул
за
сравнение
на числото X с
други числа,
които имат
същия
остатък R, както
и още, че частното
Z, в тази
постановка,
се определя като
коефициент
на кратност
на модула (за
последните
понятия
читателят
може да
прочете
подробното
изложение в раздел 3.3.5.3
на тази книга).
Точно в тази
интерпретация,
числото X
може да се
изрази чрез
коефициента
за кратност Z,
модула за
сравнение Y и
остатъка, или
още
изображението
R, така
X=Z.Y+R.
В раздел 3.2.6 на книга [1], частичният остатък, който определя последната цифра в частното, може да послужи за извеждане на следното равенство
![]()
Според даденото в началото определение, това равенство може да бъде записано така
![]()
Равенството
(3.2.9.4.1) е
забележително
с това, че изразява
как може да
се получи вторият
резултат от
операция
деление, а
именно
остатъкът Rx
от делението.
Изводът е, че
остатъкът Rx
се съдържа в
последния
частичен
остатък Rk-l+1,
който следва
да се измести
на (k-l) бита
надясно, за
да се
представи
правилно
като цяло число.
Това число е
със знак и ще
бъде
получено автоматично
в
допълнителен
код.
Необходимо
е още едно
пояснение.
Ако последното
изваждане,
при което се
получава
последният
частичен
остатък Rk-l+1, е
било успешно,
то той
съдържа
търсения остатък
Rx. Ако обаче
изваждането
не е било
успешно, то
от последния
частичен
остатък Rk-l+1
следва да се
възстанови
предидущия
частичен остатък Rk-l, в който
трябва да се
съдържа
търсения
остатък Rx.
Възстановянето
на
предидущия
частичен остатък
се постига
чрез
събиране или
изваждане на
делителя Wy, операция,
която се
избира
според
правилото,
дефинирано в
таблица 1 в
предходния
раздел, както
следва
![]()
В
крайна
сметка може
да бъде
изказан
следния
алгоритъм:
Ако
полученото
частно е нечетно
число, то
остатъкът се
съдържа в
последната
разлика.
Ако
полученото
частно е четно
число, то
остатъкът се
съдържа в
предидущата
разлика. В
този случай
се налага
възстановяване
на
предидущата
разлика.
Окончателният
остатък се
получава
след аритметическо
изместване
надясно на (k-l) бита на
съответния
частичен
остатък.
Казаното до тук ни позволява да синтезираме онази част от логическа структура, която допълва представената в предидущия раздел до следния й окончателен вид
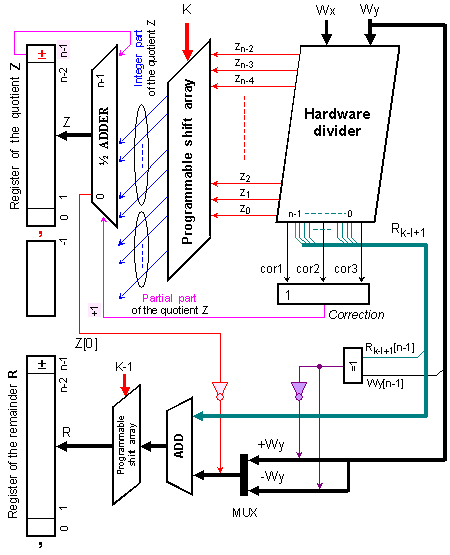
Фиг.
3.2.9.4.1. Логическа
структура на
схемния
делител,
допълнена
с елементи,
необходими
за
изчисляване
и на остатъка
С това считаме изложението на нашия проект за завършено. Разбира се има още няколко подробности, които си спестяваме. Имаме предвид например случаите, в които се налага нормализация на полученото частно след деление на числа с ляво фиксирана запетая или пък случая с препълване при деление на цели числа. Отразяването на тези тънкости в синтезираната схема изисква само добро познаване на алгоритъма.
Цялостното изпълнение на устройството за деление във вид на една единствена комбинационна схема е напълно възможно. Това превръща операция деление в едно-тактна, което я прави аналогична с операция умножение, както и с някои операции по изчисляване на елементарни функции. Това твърдение няма да представим подробно тук, но ще го опишем кратко. Необходими са само 4 регистъра – 2 два входни за входните операнди X,Y и два изходни за двата резултата Z,R. Между тези две двойки регистри се нареждат последователно следните комбинационни схеми. Най-напред върху входните регистри се поставят схеми за определяне броя на старшите незначещи цифри на операндите. Това са комбинационни схеми, които са синтезирани по наш проект, публикуван в
Със синтеза на споменатата схема читателят може да се запознае и в раздел 3.5.1 на тази книга:
http://www.tyanev.com/home.php?lang=bg&mid=18&mod=1&b=12&s=454
Формираните
от тези две
схеми числа
постъпват на
суматор,
който
изчислява
споменатото
по хода на
изложението
по-горе число
N. Резултат
на този
суматор
могат да
бъдат още
числата К и (К-1),
необходими
за
инициализация
на
следващите в
схемата
функционални
нейни части.
Операндите
постъпват
още на входа
на схемния
делител, от
изходите на
който излизат
две
комбинации.
Първата,
преминавайки
през
изместващата
матрица и
полу-суматора
½ADDER,
се записва в RGZ
като първи
резултат –
частно Z.
Втората,
представляваща
последната
разлика Rn-1, преминава
последователно
през
суматорът ADD и
изместващата
надясно
матрица и се
записва в
изходния
регистър RGR
като втори
резултат –
остатък R.
В
случай, че
схемата се
използва за
деление на
числа с
плаваща
запетая,
остатъкът
губи своя
смисъл, а
числото К
приема
стойност 0,
която прави
изместващата
матрица
прозрачна.
Представените в допълнението два числени примера илюстрират функционирането на алгоритъма и на синтезираната логическа структура.
По-долу привеждаме два числени примера, илюстриращи функционирането на синтезираната логическа структура при получаване и на двата резултата – частно и остатък.
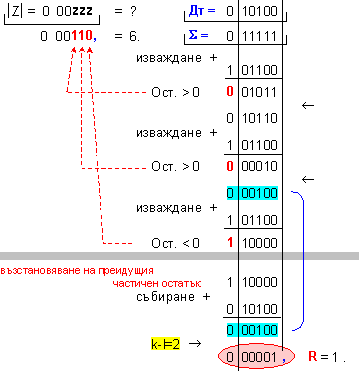
ПРИМЕР 1. Да се
изпълни
операция
деление Z=X/Y на
числата X=31 и
Y=5, които
са
представени
в разрядна мрежа
с дължина n=6[b]
. Следва да
получим този
отговор: частно
Z=6 и остатък R=1,
т.е. 31=6.5+1 .
Дм
= |X| =
0 11111 ; Дт = |Y| = 0 00101
.


N = 2 - 0 + 1 = 3
( 3
неизвестни
цифри на
частното )
k-l = 2-0 = 2 -
изместване
на 2[b] за
формиране на
остатъка.
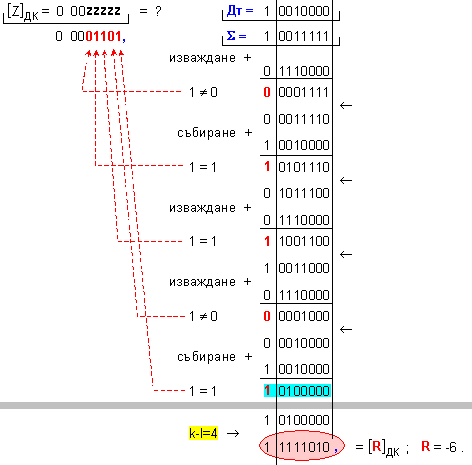
ПРИМЕР 2. Да се
изпълни
операция
деление Z=X/Y на
числата X=-97 и
Y=-7, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=+13 и
остатък R=-6, т.е. (-97)=13.(-7)-6 .
![]()
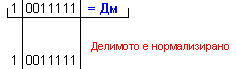

N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe на
4[b] за
формиране на
остатъка.
Следващият
раздел е:
3.2.10
Унитарни
операции ( Unitary operations )