3.3.4 Грешки при изчисления с плаваща запетая

Floating point errors

Фатални грешки на двоичната аритметика при изчисления

във форма с плаваща запетая

Основната форма, в която се представят реалните числа, това е формата с плаваща запетая. Тя е протоколирана със стандарта IEEE 754. Главното достойнство на ФПЗ е големият диапазон на представяните числа, както и простотата на изчисленията в двоична бройна система. Последната обаче е и причина изчисленията в тази форма до получаване на съвършено непредвидими резултати. Това е причината да се спрем тук подробно на тази тема, за да убедим читателя в това твърдение.

Източниците на грешки във ФПЗ са много и ние ги изследваме в много от разделите на тази книга, свързани с различните видове обработка на реалните числа. Ще припомним, че във формата Single Precision (SP) полето на мантисата е 24 битово и то позволява да се представят точно резултати, в които верни могат да бъдат до 7 десетични цифри. Форматът Double Precision (DP), в който мантисата е 53 битова, гарантира до 15 верни десетични цифри.

Десетичните числа, след преобразуване от двоична бройна система, съдържат верни цифри но и “опашки” от неверни цифри. Тези "опашки" са основен източник за грешки в резултатите от изчисления във ФПЗ. Това ще покажем тук с множество числени примери. За всички примери броят на верните десетични цифри в резултатите, е 7.

Операция събиране

Ще започнем с операция събиране. Ще събираме две реални числа X и Y, всяко от които има по 7 верни цифри:

X+Y = 0,6000006 + 0,0333987_4 = 0,6333993_4 ≈ 0,6333993

Сега ще изпълним същото изчисление с 24-битовите двоичните еквиваленти на числата, записани в мултипликативен вид:

X = 0,6000006 ≈ 1,00110011001100110100100.2^(-1) ; ·

Y = 0,0333987_4 ≈ 1,00010001100110100011110.2^(-5) .

Ако тези две числа преобразуваме обратно в десетична бройна система, ще получим следните стойности:

X = 0,6000006_198883056640625 ≈ 0,6000006_2 ;

Y = 0,03339873_9993572235107421875 ≈ 0,0333987_4 .

Както може да се види, след закръгляне до 7 позиции след запетаята, “опашките” в числата са отделени с долен подчертаващ символ ( _ ). Тези "опашки" са се получили след обратното преобразуване на двоичния код на мантисите. 24-битовата двоичната сума на двете числа е следната:

1,00110011001100110100100.2^(-1) + 1,00010001100110100011110.2^(-5) ≈

1,01000100010011001110110.2^(-1) ≈ 0,6333994 .

Същият резултат се получава при събиране на двете числа заедно с техните “опашки”:

0,6000006_2 + 0,0333987_4 = 0,6333993_6 ≈ 0,6333994 .

Както се вижда, след закръгляне до 7 значещи цифри, тук е получен резултат, различен от този, който беше получен при събиране на десетичните числа с калкулатора. Правилата за закръгляне на двоичните числа, заложени в стандарта IEEE 754, не решават проблемите на точното изчисление в примера. Причината за грешка тук се крие в съчетанието на цифри, стоящи след последните верни цифри в десетичните събираеми, а които априори нищо не е известно.

Ще разгледаме още един пример с операция събиране. Ще съберем с калкулатора на Windows следващите две числа, всяко от които има по 7 верни десетични цифри:

6543,455 + 12,34548 = 6555,80048 ≈ 6555,800 .

Сега ще представим тези събираеми в двоична бройна система във ФПЗ и 24-битова нормализирана мантиса:

6543,455 = 1,10011000111101110100100.2¹² = 6543,455_078 ,

12,34548 = 1,10001011000011100010110.2³ ≈ 12,345_48 .

Събираме тези двоични числа и закръгляме сумата до 24 бита. Така получаваме:

1,10011001101111001101000.2¹² ≈ 6555,80078125 ≈ 6555,801 .

Отново се получава реаултат, различен от този, който изчислихме с калкулатора (неверна младша цифра в резултата).

Операция умножение

Като следващ пример ще разгледаме изчисляването на произведение.

0,0654345_5.139 = 9,095402_45 ≈ 9,095402 .

Във ФПЗ числата са:

0,06543455 = 1,00001100000001010001101.2^(-4) ;

139 = 1,00010110000000000000000.2¹⁰ .

Резултатът от умножението е:

1,00001100000001010001101.2^(-4) . 1,00010110000000000000000.2¹⁰ =

= 1001,00011000011011000101 ≈ 9,095403 .

Вижда се, че в младшия разряд има невярна цифра, която е невъзможно да бъде поправена чрез закръгляне на двоичния еквивалент на резултата. Такива грешки наричаме фатални.

Операция деление

Аналогично с пример разглеждаме операция деление.

131 / 0,066 ≈ 1984,848 .

Във ФПЗ числата имат вида:

131 = 1,00000110000000000000000.2⁷ ;

0,066 = 1,00001110010101100000010.2^(-4) .

Частното от делението на тези две числа е:

1,11110000001101100100111.2¹⁰ = 1984,848_5107421875 ≈ 1984,849 .

Отново виждаме невярна младша цифра

Операция изваждане

Изваждане е операция, която напълно дискредитира идеята за използване на двоичната аритметика за изчисляване на десетични числа във ФПЗ. Нека умаляемото е числото 105,3256. Нека умалителят е 105,32. Тогава разликата е следната:

105,3256 – 105,32 = 0,0056 .

Представяме операндите в двоична бройна система във ФПЗ:

105,3256 = 1,10100101010011010110101.2⁶ ≈ 105,3255_997041015625 ;

105,32 = 1,10100101010001111010111.2⁶ ≈ 105,32 .

Резултатът от двоичното изваждане е:

1,01101111000000000000000.2^(-8) ≈ 0,005599976 .

В този резултат само старшите 3 цифри са верни.

От получаване на фатални грешки (резултат с неверни цифри) не ни спасяват и по-дългите формати, които стандартът IEEE 754 е определил, и които производителите на хардуер съблюдават. "Злото”, както вече много пъти посочихме, се корени в особеностите на двоичната бройна система, както и на аритметичните алгоритми за изпълнение на отделните операции. Колкото по-сложни са изразите, в които участват операндите, и колкото повече те се преработват, толкова повече грешки се акумулират в крайния резултат, ето защо не се учудваме на множеството опити да се излезе от тази ситуация на пълна симбиоза между двоичната бройна система и дигиталния хардуер.

Вече може да се обобщи, че аритметиката с плаваща запетая е неточна. В алгоритмите за изпълнение на операциите има неотстраними причини за загуба на точност, т.е. на значещи цифри. Както се постарахме да изясним, източниците на принципните грешки следва да се познават от програмиста много добре, тъй като тяхното "забравяне" в съчетание с непознаване на характера (степента на вярност и надеждност) на изходните данни води дори и в тривиалните алгоритмични схеми до крайно неверни резултати, до неустойчивост на програмните реализации на числените методи и не рядко до крайно опасната ситуация на зацикляне на програмата. Тогава какво остава за по-сложните изчисления!

Един от пътищата за намаляване на грешките е използване на дългите формати за представяне на данните (неизбежни за съвременните устройства), но от това е възможно да се губи скорост в обработката и да се изразходва много памет.

В устройствата за работа с плаваща запетая, по време на изчисленията се използува вътрешен формат за представяне на числата, различен от този, който наричахме Memory Format, който по същество представлява възможно най-дългият за разрядната мрежа формат, за което ще бъде писано по-късно тук. При това, ако програмистът е декларирал например променливите А,B,C и D като променливи от тип SP (single precision) и е запрограмирал израза (A*B)/C, чиято стойност да бъде присвоена на D, резултатът от умножението A*B може да се окаже твърде голям и непредставим във формата SP. В същото време, ако това произведение се представи като междинен резултат (ненужен на програмиста) във вътрешния разширен формат, то след операцията деление с числото С е възможно частното отново да стане представимо във формата SP. Ето защо разширеният вътрешен формат, който има значително по-голям диапазон на представимите числа (вижте фигура 1.1.6.2.4 и таблица 1.1.6.2.1), в повечето случаи намалява вероятността от прекъсване на потребителската програма по причина на препълване или антипрепълване на междинните резултати и е желан от програмиста. В това отношение съществено влияние оказва скритият бит. Всичко казано току що е свързано не само с възможностите на полето на мантисата, а дори в по-силна степен с възможностите на полето на порядъка, което от 8 битово във формат SP става 15 битово в разширения формат EP на разрядната мрежа.

Намаляване на грешките още може да се постигне чрез правилна схема на закръгляне, избирана в съответствие с изчислителната схема и характера на данните.

Така например, традиционното разбиране на процеса закръгляне се изразява с функцията round, която още се нарича закръгляне към най-близкото представимо число. За да се реализира процесът на закръгляне, изразен чрез тази функция, се изисква представяне и действие с константата

която по същество представлява половината от стойността на основата на бройната система, в която е представено числото (const=1,4,5,8 и пр., съответно за двоична, осмична, десетична и шеснадесетична). Теглото на тази константа, поставена в съответната позиция (най-старшата за непредставимата част, фактически е половината от теглото на най-младшия разряд на възможната за представяне мантиса, което илюстрира следващата рисунка.

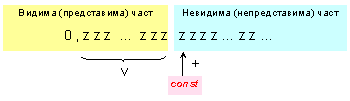
Фиг. 3.3.4.1. Позиция на константата за закръгляне на числото до разряд № v (според 3.3.1.14)

Представянето на тази величина изисква в изчислителното устройство, вдясно от полето на мантисата (в непредставимата част на числото), да има поне още един допълнителен разряд. Това означава, че всички алгоритми за работа с плаваща запетая трябва да изчисляват мантисата на резултата поне с още един допълнителен разряд.

На практика в разрядната мрежа на широко разпространените аритметични процесори за работа с плаваща запетая (двоична бройна система) са добавени три младши допълнителни разряда, както е показано на фигура 3.3.4.2, които спомагат за по-доброто закръгляне на мантисата в рамките на половин младша единица [има се предвид бит №(m-1)].

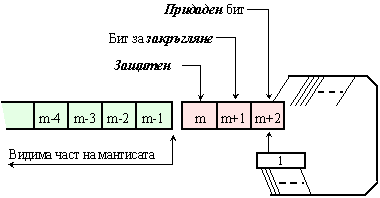
Фиг. 3.3.4.2. Схема на допълнителните разряди в разрядната мрежа

Защитният бит се налага от алгоритмите за умножение и деление, където както показахме, денормалността на мантисата както отляво, така и отдясно, не може да бъде повече от един бит (виж (3.3.2.3) и (3.3.3.2)). В тези случаи допълнителният защитен разряд спомага да не губим най-младшата цифра при следващото изместване на 1 бит.

След защитния бит следва битът за закръгляне.

Придаденият бит получава стойност в дадения формат на значещата част (както е показано на схемата от фигура 3.3.4.2) чрез логическата функция ИЛИ от всички изчислени цифри вдясно от позицията с номер (m+1) и в този смисъл показва дали в онази част от числото, която не се представя въобще, има значещи цифри. В този смисъл стойността в бит (m+2) показва да ли частта от числото вдясно от този бит е нула или не.

Всеки реален резултат може да се разглежда по следния начин:

където Z е точният математически резултат, а ∆(Z) абсолютната грешка, допусната в процеса на закръгляване.

Описаната чрез функцията round процедура на закръгляване, която обикновено е установена по подразбиране, по същество представлява прибавяне на единица към стойността в бита за закръгляне след изпълнение на съответния алгоритъм, т.е. прибавяне на описаната по-горе const. Грешката при изчисления в този режим е знакопроменлива. Този режим осигурява възможно най-точната и статистически неизместена оценка на резултата. В този режим съществува един специален случай, когато полученият резултат се намира точно по средата между две съседни представими числа, което е особеност единствено на двоичната бройна система. Обикновено в тази ситуация се извършва закръгляне към по-голямото, в следствие на подаването на +1 в бита за закръгляне, което довежда до ненужно изместване на стойността на резултата. За да бъде то изключено, в процесора с плаваща запетая, при (b-a=c-b) се осъществява закръгляне към четното от числата а и с, т.е. към онова число, в младшия бит на което има нула. Следователно "средните" резултати се закръглят и нагоре и надолу. Такъв начин на закръгляне се нарича "неизместено закръгляване към най-близкото четно".

Освен тази схема на закръгляване се прилагат и други схеми. Това са схемите:

P закръгляне в посока към нулата (отрязване на излишните цифри). Тази схема на закръгляне се изразява от функцията trunc(X,v), която има вида:

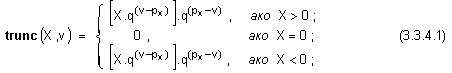
Тази функция се отличава от round само по това, че в нея липсва константата const. При такава схема на закръгляне, модулът на числата се представя винаги с недостиг по отношение на математическата им стойност. Тази схема на закръгляване се прилага при целочислените изчисления, провеждани в устройството за работа с плаваща запетая.

P Закръгляне към най-близкото представимо по-малко число.

P Закръгляне към най-близкото представимо по-голямо число.

Последните два начина на закръгляване имат значение при използуването на така наречената интервална аритметика.

В съвременните процесори за работа с плаваща запетая режимите на закръгляване се управляват от съдържанието на специално двубитово поле RC (Rounding Control). Битовете за управление на схемата за закръгляне в процесорите на Intel например са 2 и се намират в регистъра за управление CW на FPU и назначават споменатите по-горе четири схеми в следното съответствие:

· RC=00 – закръгляне към най-близкото четно;

· RC=01 – закръгляне надолу (към -∞);

· RC=10 – закръгляне нагоре (към +∞);

· RC=11 – закръгляне към нулата.

Степента, в която математическите закони са в сила при изпълнение на операции с плаваща запетая, се оценява не с абсолютните грешки, а с относителните. Разбира се, ако за потребителят абсолютната грешка има определен смисъл, тя също следва да се изчисли. Определението на относителната грешка (3.3.1.6) обаче не може да се приложи непосредствено, тъй като абсолютната математическа стойност на резултатите практически е неизвестна. Ето защо най-често относителната погрешност се изразява чрез отношението на абсолютната грешка към представената в разрядната мрежа стойност:

Абсолютната грешка от своя стана се оценява чрез функцията round (т.е. чрез схемата за закръгляне, която се прилага в конкретния случай) така:

От горния израз се получава окончателният вид на оценката за относителната погрешност:

Използувайки тези означения, могат да бъдат изведени следните изрази за относителните грешки, допуснати в резултата при изпълнение на четирите аритметични операции:

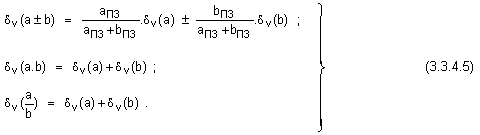
При небрежно отношение на програмиста към поведението на данните в хода на изчислителния процес могат реално да настъпят следните грешки:

1. Абсолютната стойност на грешката на разликата на две близки по абсолютна стойност числа, може да надвиши абсолютната стойност на резултата. Възможно е полученият резултат да се отличава от истинския на няколко порядъка!

2. Ако при деление делителят е много по-малък от делимото, принципните грешки от представянето на числата могат да доведат до това, че частното силно ще се отличава от истинския резултат!

3. При сравнение на две приблизително еднакви числа резултатът зависи в много по-голяма степен от грешките в числата при тяхното представяне, отколкото от самите числа! В този случай отношенията (.LT., .LE., .GT., .GE., .EQ., .NEQ.) губят смисъл и ако те се използват за разклонения в програмите могат да доведат до погрешен ход и резултати на изчислителния процес!

Опитният програмист никога не изпитва желание да проверява изпълнено ли е равенството

съзнавайки колко малка е вероятността за такова събитие, особено в случаите когато a_пз и b_пз са резултати, получени след различни изчисления. Вече имахме повод да споменем в пункт 3.3.1 за опасността, която застрашава всеки итерационен алгоритъм от надеждата, че процесът може да се контролира с проверка на отношение от вида:

Много по-разумно в подобни случаи е да се контролира отношението

но тъй като програмистът не знае отнапред порядъка на наблюдаваната величина A, още по-правилно е да се очаква изпълнението на неравенство от следния вид:

където величината e (машинното епсилон) е пропорционална на порядъка p_A на контролираната величина.

Съотношението (3.3.4.7) по същество изразява приблизителния характер на изчисленията с плаваща запетая, където отношението "равно" изгубва своя абсолютен характер и на негово място влиза "приблизително равно", т.е. равенство с определена (приемлива) степен на неопределеност. В този смисъл при работа с плаваща запетая операция "сравнение" (както вече отбелязахме) губи онова значение, което тя има в аритметиката с фиксирана запетая. По тази причина проверката на отношенията =,<,> и др. могат да доведат до силни заблуждения относно хода на изчислителния процес!

Съществува още един подход към проблема за оценка на погрешността на даден резултат, който се нарича интервална аритметика. Според нея една машинна стойност А се дефинира с две числа А_дг и А_гг на долната и горната граници на интервала [А_дг , А_гг]. За да се определи интервалът, в който гарантирано се намира истинската стойност на едно математическо изчисление, програмистът е длъжен да запрограмира това изчисление два пъти. В първия участък на програмата, както изходните величини, така и всички междинни резултати, трябва да участвуват в изчисленията с онези свои граници, според които ще се получи долната граница на крайния резултат, а във втория участък на програмата изчислението се извършва с противоположните граници така, че да се получи горната граница на крайния резултат. По време на тези изчисления се налага да се различават абстракциите +0, -0, +∞ и -∞. В тези изчисления програмистът трябва да се съобразява с изпълнението на тъждествата, които бяха представени по-горе. Много автори обаче са твърде песимистично настроени спрямо надеждността на окончателната оценка, особено ако полученият за нея интервал е значително разширен. Мотивите им се съдържат в твърде сложните взаимни зависимости между междинните резултати, особено в случаите, когато се работи с итерационни числени методи. За съжаление тези проблеми излизат извън нашите интереси и тук ние няма да ги изследваме.

Абстракцията безкрайност се генерира по време на изчисленията в два случая: при препълване и при деление на нула. В цифровите процесори за работа с плаваща запетая, които читателят най-често среща, могат да бъдат въведени два режима за работа с абстракциите безкрайност и нула, които програмистът може да използува - свързан режим и проективен режим. Режимите се установяват в зависимост от специален бит IC (Infinity Control). Двата режима произлизат от двете интерпретации на числовата ос, показани на фигура 3.3.4.2:

Фиг. 3.3.4.2. Кръгова и интервална интерпретация на числовата ос

1. В проективен режим се различава една нула и една безкрайност, т.е. нулата и безкрайността са беззнакови стойности. Безкрайността се определя като число, което е по-голямо от всички други представими числа по модул. В този режим при опит да се изпълни операция сравнение на безкрайност с представимо число се получава особен случай, наречен "невалидна операция". При сравнение на две безкрайности се получава равенство. При събиране и изваждане на две безкрайности отново се получава случаят "невалидна операция", а при събиране и изваждане на представимо число и безкрайност, резултатът е безкрайност.

2. В свързан режим процесорът различава числата +0 и -0, както и числата +∞ и -∞. Стойността +∞ се определя като число, което е по-голямо от всички представими числа, а стойността -∞ като число, което е по-малко от всички представими числа. Така, примерно за операция събиране, в таблица 3.10 са дефинирани следните резултати:

Таблица 3.3.4.1 Определяне на знака

Резултат	Коментар
(+0) + (+0) = +0
(-0) + (-0) = -0
(+0) + (-0) = ±0	знакът се определя от схемата на закръгляване: плюс при закръгляване към най-близкото представимо; минус при закръгляване надолу
(-0) + (+0) = ±0
(+X) + (-X) = ±0	знакът се определя от схемата на закръгляване: плюс при закръгляване към най-близкото представимо; минус при закръгляване надолу
(-X) + (+X) = ±0
(+0) + (±X) = X	знакът на резултата не се променя
(±X) + (±0) = X	знакът на резултата не се променя
(+∞) + (+∞) = +∞
(-∞) + (-∞) = -∞
(+∞) + (-∞)	недействителна операция
(-∞) + (+∞)	недействителна операция
(±∞) + (±X) = ∞	знакът на резултата приема стойността на знака на операнда безкрайност
(±X) + (±∞) = ∞

Както се вижда в този режим разрешена операция е събирането на две безкрайности с еднакъв знак:

(+∞) + (+∞) = +∞

и изваждането на две безкрайности с различен знак:

(-∞) - (+∞) = -∞

При сравнение на двете нули, същите се признават за равни, но при деление генерират знакоопределена безкрайност:

X / (+0) = +∞ ; (-X) / (+0) = -∞;

X / (-0) = -∞ ; (-X) / (-0) = +∞.

Очевидно се определят резултатите при работа с безкрайност:

X / (+∞) = +0 ; (-X) / (+∞) = -0 ; и т. н.,

X.(+ ∞) = +∞ ; (-X).(+ ∞) = -0 ; и т. н.,

(+∞) / X = +∞ ; (-∞) / X = -0 ; и т. н.,

(+∞).(+∞) = +∞ ; (-∞).(+∞) = -∞; и т. н.,

където X е X>0 и не е безкрайност.

Операция "сравнение" в този режим е различна от тази в предходния и за всяко число X е изпълнено неравенството

-∞ < X < +∞ .

По аналогичен начин във всеки реален процесор за всяка операция са известни тези специални резултати, с които читателят може да се запознае от съответната литература.

Освен коментираните по-горе стойности могат да се получат така наречените нечислови стойности NAN. Тези стойности се познават по това, че всички битове в полето на характеристиката са 1, а мантисата е различна от нула. Ако операнд в една аритметична операция е нечислова стойност, тогава за резултат се формира нечислова стойност и заедно с това се установява признак на “невалидна операция”. Програмистът може да използва този признак косвено по следния начин:

· След предварително зареждане на данновите поле с начална стойност NAN, да се използва признакът за грешка при опит да се използва поле, което не е било заредено с числова стойност;

· След предварително зареждане на елементите на един масив с NAN, чиято мантиса съдържа поредния номер на елемента от масива, всеки опит за обръщение към нечислова стойност от масива не само ще ни подскаже, че масивът не е зареден с числа, но можем да установим кой точно негов елемент не е число.

Както вече беше споменато в глава 1, при изпълнение на операции с плаваща запетая с цел по-съвършено управление на изчислителния процес и по-гъвкаво използване на изключителните стойности, получаващи се като резултат, се налага откриването и сигнализирането им чрез апаратни средства. Тези изключителни събития се наричат просто изключения. За всяко изключително събитие са предвидени два бита - флаг на признака и маска. Ако флагът не е маскиран се генерира прекъсване. Програмата за обслужване на прекъсването отчита всички особености на разрядната мрежа, на вградените алгоритми за изпълнение на аритметичните операции и се основава на задълбочен числен анализ. Не се препоръчва на непрофесионалисти в тези области да подменят или модифицират тези програми.

Ако флагът за изключително събитие е маскиран, изключителните резултати се обработват на микропрограмно ниво, с цел извършване на подходящите корекции. При това не се променя стойността на флага маркирал изключителното събитие.

Ето по-конкретно изключителните събития и техните означения (според INTEL):

1. Неточен резултат. Резултатът не може да се представи точно в крайния формат. Установява се флагът РЕ=1 (precision error). Ако флагът е маскиран, се извършва миропрограмно закръгляне според текущо назначената схема за закръгляне и програмата продължава своето изпълнение. Ако флагът не е маскиран, се генерира прекъсване.

2. Антипрепълване. Установява се флагът UЕ=1 (underflow error). Събитието настъпва когато резултатът е много малък и не може да се нормализира. Ако флагът на това събитие е маскиран, работата на програмата продължава с този резултат (с недостиг). Ако флагът не е маскиран, резултатът се записва във вътрешен регистър и се генерира прекъсване.

3. Препълване. Установява се флагът OЕ=1 (overflow error). Резултатът, който се получава, е твърде голям по абсолютна стойност за възможностите на разрядната мрежа (или за крайния формат). Ако флагът е маскиран, за резултат се приема знакова безкрайност. Ако флагът не е маскиран, резултатът се записва във вътрешен регистър и се генерира прекъсване.

4. Деление на нула. Установява се флагът ZЕ=1 (zero error). Събитието настъпва, когато делимото е представимо число, а делителят е нула. Ако флагът на събитието е маскиран, за резултат се приема знакова безкрайност. Ако флагът не е маскиран, се генерира прекъсване преди изпълнение на операцията.

5. Денормализиран операнд. Установява се флагът DЕ=1 (denormalized error). Този флаг се установява, когато постъпва операнд, чиято мантиса не е нормализирана. Ако маската на флага е установена, операцията се разрешава и се изпълнява с този операнд. Ако маската не е установена, операцията не се изпълнява и се генерира прекъсване.

6. Недействителна операция. Установява се флагът IЕ=1 (instruction error). Това събитие може да настъпи по две причини:

· Зареденият операнд е NAN (не е число). Ако събитието е маскирано, за резултат се записва операндът NAN. Ако и двата операнда са NAN, за резултат се приема по-голямото от двете NAN.

· При математическа недефинираност, като например 0/0, ∞/∞ и др. при обръщение към пълен стек (става дума за стека в устройството) или е празен. Ако флагът на събитието е маскиран, в полето за резултат се записва специална нечислова стойност, по която може да се разпознае събитието. Получаването на математическа неопределеност е критична грешка и изпълнението на програмата трябва да се прекрати.

И в двата случая ако флагът не е маскиран се генерира прекъсване без изпълнение на операцията.

В устройството за работа с плаваща запетая има 16-битов регистър за управление на точността и закръглящата схема. Съдържанието на този регистър може да се зарежда с машинна команда (FLDCW за Intel). Структурата на този управляващ регистър е показана на следващата фигура.

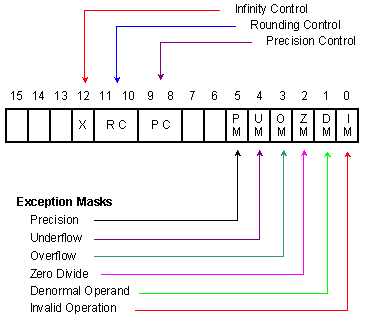
Фиг. 3.3.4.3. Структура на регистъра за управление на точността и закръглящата схема

Необходимо е да отбележим, че коректният читател следва допълнително да детайлизира и конкретизира изложеното по-горе за онзи модел на процесора, с който работи.

Следващият раздел е:

3.3.5 Примерни логически структури на устройства за работа с плаваща запетая

( Exemplary logical structures of floating-point devices )