3.3.5.2 Логическа структура на устройство за работа с ПЗ и комбинационен суматор

FPU with combination adder

Следващата примерна логическа структура за работа с плаваща запетая е представена на фигура 3.3.5.2.1. Тя се характеризира с това:

1. Че е основана на един суматор от комбинационен тип;

2. Че разрядната мрежа е структурирана в съответствие със стандарта IEEE-754 подробно изложен в глава 1 (вижте пункт 1.1.6.2 и фигура 1.1.6.2.4);

3. Че аритметичните операции са реализирани чрез алгоритмите за обработка на операндите по модул;

4. Че при нейния синтез са приложени водещите за нас предпоставки, изложени в началото на глава 3.

Представената логическа структура е удобна за детайлно изучаване на изложените вече алгоритми. Функционирането й е илюстрирано чрез множество примери в книга [2]. Изложените там примери изясняват аритметиката с изместен порядък както и аритметиката с техниката на скрит бит.

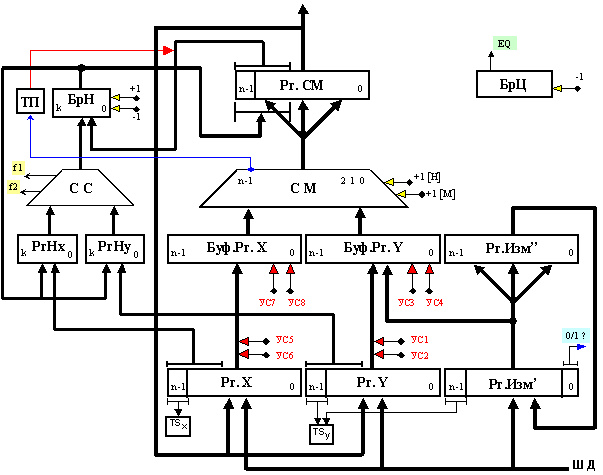
Фиг. 3.3.5.2.1. Примерна логическа структура за работа с плаваща запетая

по стандарта IEEE-754

В показаната примерна структура, суматорът СМ е с дължината на разрядната мрежа - n [b]. Той е свързан по вход и по изход с основните логически възли, необходими за организиране на операция събиране и изваждане - РгХ, РгY, РгСМ, както и с буферните регистри БуфРгХ и БуфРгY. С добавяне на изместващия регистър РгИзм и косите връзки за ляво и дясно изместване, логическата структура става пригодна за изпълнение и на операциите умножение и деление. Допълнителната група от логически възли в лявата част на рисунката, включваща брояч на характеристиките БрН, схема за сравнение (цифров компаратор) СС, регистри за порядъците РгНх и РгНу, е необходима за сравнение на порядъците и за процеса на нормализация.

Трябва да се припомни, че в използуваната в случая структура на разрядната мрежа, най-левият разряд съдържа знака на числото (±), следва характеристиката Н, а неговата мантиса М се намира вдясно от нея, т.е. структурата й е (±Н,М).

1. Изпълнение на операция събиране (изваждане).

Операндите X, Y се приемат във входните регистри РгХ и РгY, т.е. операцията е реализирана като двуместна. Заедно с това, знаците на операндите се запомнят в тригерите TSx и TSy. Ако операцията е изваждане в TSy се зарежда инверсната стойност на знака на втория операнд Y. В същото време изместените порядъци, т.е. характеристиките, се изпращат съответно в РгНх и РгНу, след което знаковите разряди във входните регистри РгX[n-1] и РгY[n-1], както и полетата на характеристиките РгX[Н] и РгY[Н], се нулират. В резултат на това във входните регистри РгX и РгY остават само модулите на мантисите. За да се извърши проверка на мантисите, същите се препращат последователно в буферните регистри и оттам на суматора, към чийто изход са включени схемите за формиране на признаците. Ако някоя от мантисите се окаже равна на нула, то за резултат в РгСМ се приема ненулевият операнд и операцията завършва. Ако в тази ситуация при операция изваждане нулевият операнд се окаже умаляемото, то за резултат се приема умалителят, но с обратен знак.

Ако обаче и двете мантиси са различни от нула, се изпълнява процедурата по изравняване на порядъците. По резултатите от сравнението на характеристиките в схемата за сравнение СС, се взема решение за съответните микрооперации. Тук е необходимо да се поясни, че сравнението на изместените порядъци се осъществява като логическа операция "проверка на отношение", тъй като това отношение е еквивалентно на отношението на самите порядъци. За целта обаче в случая, на изместените порядъци се гледа като на числа без знак и тяхното отношение се установява с помощта на цифров компаратор.

Възможните отношения се разпознават с помощта на следните две логически функции:

чийто логически израз има вида:

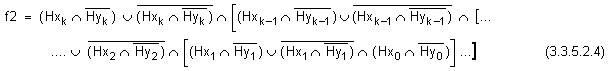
където

са цифрите от характеристиките на операндите.

Тук следва да поясним, че k-битовото поле на характеристиките тук е допълнено отляво със знаковия бит на входните регистри, ето защо регистрите на характеристиките имат дължина (k+1) бита.

При сравнение на порядъците са възможни пет случая:

1. (p_x-p_y) > (m-1) , (операнд Y губи значимост) или

2. (p_y-p_x) > (m-1) , (операнд X губи значимост) или

3. (p_x-p_y) = 0 , (етапът за изравняване на порядъците отпада) или

4. (p_x-p_y) < (m-1) , (по-големият порядък е на числото X ) или

5. (p_y-p_x) < (m-1) , (по-големият порядък е на числото Y ) .

Изравняването на порядъците чрез манипулация на характеристиките в логическата структура практически протича по следния начин. След зареждане на характеристиките в допълнителните регистри РгНх и РгНу те попадат в схемата за сравнение СС, която чрез функциите f1 и f2 веднага определя коя е по-голямата от тях. Ако например резултатът от сравнението е f1=0 и f2=0, то по-голямата характеристика е Н_у. В този случай по-малката характеристика Н_х се зарежда в брояча на характеристиките БрН, където може да бъде модифицирана. Заедно с това мантисата Мх се изпраща в БуфРгХ и оттам през суматора, по косата връзка и РгСМ се измества надясно.

И така, при всяко изместване на мантисата Мх, в БрН се прибавя единица, след което неговото съдържание се връща по обратната връзка в РгНх, от където то постъпва в схемата СС за ново сравнение с Н_у. Последователността от микрооперации сравнение, изместване на мантисата и нарастване на по-малката характеристика Н_х се повтаря до настъпване на равенството Н_x=Н_у, разпознавано от схемата СС (f1=1, f2=0). Това е края на етапа изравняване на порядъците.

За да се разпознаят първите два случая на отношението на порядъците и да не се правят излишни цикли за изместване надясно когато изместващата се мантиса вече напуска разрядната мрежа, в началото на алгоритъма, в брояча на циклите БрЦ се установява константата (m-1). При всяко изместване на мантисата, от брояча на циклите БрЦ се изважда единица и ако той се нулира преди да е настъпило изравняване на порядъците, за резултат се взема вторият операнд Z=Y, който в случая има по-големия порядък и операцията завършва.

Ако при първоначалното сравнение се окаже, че f1=0 и f2=1, тогава по-голямата характеристика е Н_х. В този случай се постъпва аналогично – в брояча на характеристиките БрН се зарежда по-малката характеристика Н_у. На последователно изместване надясно се подлага мантисата Му, като съдържанието на БрН се увеличава с единица, докато настъпи равенство между съдържанието на РгНх и на РгНу. Ако при това, в едновременно манипулирания брояч БрЦ настъпи нулиране, това означава, че е на лице първият случай на отношение между порядъците. Тогава за резултат се приема първият операнд Z=Х и операцията завършва.

В крайна сметка, в брояча на характеристиките БрН винаги се оказва по-голямата характеристика, а във входните регистри РгX и РгY - подготвените за събиране мантиси. Самото събиране (изваждане) на мантисите се извършва в суматора, в участъка на цифровата част на мантисата.

Алгоритъмът за събиране има особеностите, наложени от правия му код - знаците на операндите все още се съхраняват в тригерите TSx и TSy, а във входните регистри се съдържат само модулите на мантисите. Ето защо е необходимо да се установи каква аритметична операция трябва да бъде изпълнена и ако е възможно, да се спестят микрооперациите за работа с допълнителен код. За целта се сравняват знаците на операндите, при това не бива да се забравя, че знакът на втория операнд е бил инвертиран в тригера TSy, в случай на операция изваждане. Така от гледна точка на основната алгебрична операция, операндите са в известна степен подготвени за аритметическо събиране. Възможните случаи са два:

· Ако знаците са еднакви, в суматора се извършва събиране на модулите. В знаковия разряд на резултата РгСМ[n-1] се приема един от знаците на операндите, например от TSy. Така мантисата на резултата се получава окончателно в прав код;

· Ако знаците са различни, следва да се извърши операция събиране, но с предварително преобразуване на отрицателната мантиса в допълнителен код. На изхода на суматора резултатът ще се получи в допълнителен код.

Необходимите в този случай микрооперации са следните: В буферния регистър на отрицателната мантиса се зарежда инверсното съдържание на съответстващия му входен регистър. Например, ако (TSx)=1, то БуфРгХ=not(РгX). Ако в същото време в нулевия разряд на суматора се подаде преносът +1[M], а (БуфРгY)=0, то на неговия изход ще се получи

Така подготвената в допълнителен код мантиса се изпраща по обратната връзка във входния регистър, след което се изпълнява операция събиране с допълнителния код на другата мантиса. Сумата от мантисите се получава на изхода на суматора в допълнителен код. Тъй като мантисата трябва да бъде представена в прав код, чрез РгСМ и обратната връзка тя се записва в РгY, унищожавайки по този начин втория операнд. Ако знакът на тази мантиса е положителен, тя остава в този си вид. Ако обаче знакът й е отрицателен, той се записва временно в TSy, след което по описания по-горе начин тя се превръща в прав код, т.е. получава се нейният модул.

Във финалния етап, ако мантисата на сумата, т.е. на резултата, не е нормализирана, чрез косите връзки на суматора се извършва необходимото й изместване, а компенсирането на порядъка се извършва в брояча на характеристиките БрН. Тази процедура се съпровожда с генериране на всички признаци, характеризиращи резултата, който се сглобява в изходния регистър РгСМ от мантиса, от характеристиката и от знак на числото. Трите елемента се приемат съответно от изхода на суматора СМ, от брояча БрН и от TSy .

2. Изпълнение на операция умножение.

Алгоритъмът за умножение на числа с плаваща запетая беше подробно разгледан в пункт 3.3.2. Неговата реализация в примерната логическа структура от фигура 3.3.5.2.1 в случая се характеризира с това, че съмножителите са представени с изместени порядъци, което създава известни затруднения при формирането на характеристиката на произведението. В представената структура множимото трябва да бъде прието в РгХ, а множителят - в изместващия регистър РгИзм. Входният регистър РгY се използува за натрупване на междинните суми.

Първоначално, след приемане на операндите в устройството, техните знаци се запомнят в тригерите TSx и TSy и знаковите разряди във входните регистри се нулират: РгY[n-1]:=0 и РгИзм[n-1]:=0. Така във входните регистри остават характеристиките и модулите на мантисите на операндите. Тези два елемента на числата се обработват поотделно – характеристиките, като представители на порядъците, трябва да се съберат, а мантисите – да се умножат. В структурата на разглежданото устройство, за разлика от устройството с натрупващи суматори, има само един комбинационен суматор, ето защо обработката се извършва последователно.

Започва се с обработката на характеристиките – в буферните регистри БуфРгХ и БуфРгY в участъка [(n-1)…(n-k-2)] се зареждат двете характеристики, съответно от РгХ[Н] и от РгИзм[Н]. При това на изхода на суматора, в същия участък, се получава тяхната сума: (S=Н_х+Н_у), която се записва в същия участък на РгСМ. Според определението за характеристиката (1.1.6.2.17) се получава сумата:

която (според същото определение) като характеристика на произведението е принципно невярна, тъй като съдържа отместването D един път в повече. За да се получи необходимата характеристика, получената сума трябва да се коригира. Отстраняването на излишъка се постига апаратно, в процеса на пренасяне на получената сума от изхода на суматора до записването й в брояча на характеристиките БрН. Синтезът на логическата схема, с помощта на която се постига необходимата корекция, е изложен по-долу.

Ще отбележим първо, че всички възможни ситуации при събиране на порядъците, разгледани в пункт 3.3.2, сега трябва да се интерпретират в светлината на определението за изместен порядък и заедно с необходимостта от корекция на горната сума. За целта k-разрядното поле на характеристиката, се разглежда на изхода на суматора съвместно със знаковия разряд на числото, т.е. това е споменатият вече (k+1)-битов участък, заемащ разрядите от [n-1] до [n-k-2]. В този участък на разрядната мрежа се получава (k+1)-битова сума от две k-битови числа без знак. От гледна точка на алгоритъма за умножение на числа с плаваща запетая, в полето на порядъка са възможни 4 случая:

1. Сумата S съответства на положителен порядък (p_z>0), получен без препълване

2. Сумата S съответства на отрицателен порядък (p_z<0), получен без препълване

3. Сумата S съответства на сума от порядъци с положително препълване

4. Сумата S съответства на сума от порядъци с отрицателно препълване

При анализа на възможните на изхода на суматора суми ще имаме предвид, че на представим положителен порядък съответства характеристика, която като k-битово число, се намира в интервала

и като число има следния общ вид:

1 hhh … hh ,

а на отрицателен порядък съответства характеристика, която като k-битово число, се намира в интервала

и като число има следния общ вид:

0 hhh … hh .

Случай първи: (положителен порядък без препълване)

Характерното за получената в този случай сума е увереността, че пренос в разряд №(k-1) на полето на характеристиката не е възможен, тъй като стойностите на порядъците по модул са малки. В резултат на това сме уверени за предварителните стойности в двата най-старши разряда на k-битовата сума, където се очаква комбинацията 10. Това твърдение се доказва с помощта на неравенство (3.3.5.2.6) така: сумата от две характеристики, класифицирани в този случай, е възможна в интервала

който може да се изрази така:

където p_k-1 изразява теглото на преноса от (k-1)-вия разряд на сумата. Последното неравенство доказва наличието на този пренос при всички суми от разглеждания случай, ето защо резултатът от събирането може да се изрази по следния общ начин:

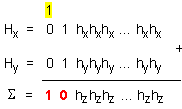
От рисунката ясно се вижда, че цифровата част на резултата съдържа (k-1)-битовата сума от порядъците

а в старшите два разряда - сумата (D+D)=2D.

Останалите три случая ще представим по-кратко, като се надяваме, че тяхното доказателство няма да затрудни амбициозния читател.

Случай втори: (отрицателен порядък без препълване)

При анализа на този случай имаме увереността, че ще възникне пренос в разряд №(k-1) на полето на характеристиката. В резултат на това сме уверени за предварителните стойности в двата най-старши разряда, където се очаква комбинацията 01. Така резултатът от събирането може да се изрази по следния общ начин:

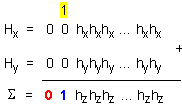
Случай трети: (положително препълване в полето на порядъка)

В този случай стойностите на порядъците са големи по модул и възникването на преноси от разряд №(k-2) и от разряд №(k-1) е неизбежно, което е изразено в следващата рисунка:

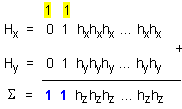
Приемайки че порядъците са положителни и в същото време големи по модул това означава, че имаме предвид настъпване на положително препълване в полето на порядъка, което следва еднозначно да свързваме със старшата комбинация на сумата, която е показан на рисунката.

Случай четвърти: (отрицателно препълване в полето на порядъка)

В този последен случай стойностите на порядъците също са големи по модул (но са отрицателни числа), което означава, че съответстващите им характеристики ще бъдат малки по модул числа. Последното означава, че възникването на пренос в разряд №(k-1) е невъзможно. Така сме уверени, че комбинацията в старшите два разряда на сумата ще бъде 00, което е изразено в следващата рисунка:

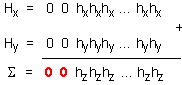
Приемайки че порядъците са отрицателни и в същото време големи по модул това означава, че имаме предвид настъпване на отрицателно препълване в полето на порядъка, което следва еднозначно да свързваме със старшата комбинация на сумата, която е показан на рисунката.

В крайна сметка изложените току що резултати, получени непосредствено след събиране на характеристиките, могат да се обобщят и тълкуват според следващата таблица 3.3.5.2.1.

Таблица 3.3.5.2.1.1 Признаци на порядъка

V - препълване в полето на порядъка	СМ [n-1, n-2]	Сумата S съответства на	Признаци на операцията преди нормализация
1 (отрицателно)	0 0		антипрепълване
0	0 1
0	1 0
1 (положително)	1 1		възможно е препълване при плаваща запетая

И така, получената сума S е принципно невярна и следва да се поправи като от нея се извади числото D. Освен това трябва да се отчете и стойността на самата сума, която е число без знак, което може да е получено с препълване и следователно е невярно. Това усложнява значително задачата за формиране на характеристиката. Не бива да забравяме, че в последния етап на алгоритъма (нормализация на резултата) е възможно да се наложи нейното допълнително модифициране, което може да се извърши само в брояча на характеристиките. Ето защо всички поправки, които ще се извършват върху получената сума следва да станат по пътя й от изхода на суматора СМ до входа на БрН.

Ще се спрем най-напред на случаите с препълване. Препълването в тези условия не може да се открие с помощта на функциите (1.2.3), (1.6.2.18) или (1.6.2.19), ето защо това се прави по данните в таблица 3.3.5.2.1. Така за препълването, което се фиксира в отделен тригер ТП, се получава следната логическа функция:

Следва да се спрем на поправката на сумата. Изваждането на излишното отместване - числото

може да се изрази така:

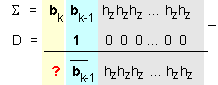
От горната рисунка се вижда:

1. Че младшите (k-1) разряда на сумата остават непроменени преминавайки в разликата, следователно те могат да се запишат в БрН директно.

2. Резултатът в разряд №(k-1) може да се получи чрез логическа инверсия на най-старшия бит на сумата.

3. И на края под въпрос остава съдържанието на знаковия бит, който е №k в номерацията на полето на характеристиката или №(n-1) в номерацията на суматора.

Истинната стойност на знаковия бит на сумата, като предварителна стойност на характеристиката на произведението, зависи от две неща:

· От това дали е открито препълване, т.е. какво е фиксирал тригерът ТП;

· И от получената в този бит стойност b_k.

Като се отчете необходимата стойност за да е в сила съответствието, което е представено в третата колонка на таблица 3.3.5.2.1, то истинната стойност, която трябва да се запише в k-тия разряд на БрН, се определя от следната логическа функция:

В резултат на всичко казано до момента, получената на изхода на суматора СМ сума от двете характеристики, се записва в брояча на характеристиките БрН по шина, която извършва описаната метаморфоза, превръщайки я в предварителна стойност на характеристиката на произведението. Шината има следната принципна логическа схема:

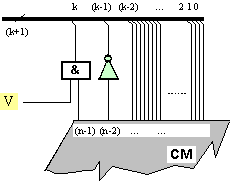
Фиг. 3.3.5.2.2. Принципна схема на шината за връзка между СМ и БрН

След записване на получената от суматора сума в брояча на характеристиките с помощта на шината, представена на фигура 3.3.5.2.2, тълкуването на предварителната стойност на характеристиката на произведението е представено в следващата таблица 3.3.5.2.2

Таблица 3.3.5.2.2 Признаци на порядъка

Фиксирано в ТП препълване	СМ[n-1,n-2]	БрН[k,k-1]	Характеристиката съответства на	Признаци на операцията преди нормализация
1	0 0	0 0		антипрепълване
0	0 1	0 0
0	1 0	0 1
1	1 1	1 0		възможно е препълване при плаваща запетая

Запис в БрН не се извършва единствено в случая на отрицателно препълване. Последното може да се разпознае по двете нули в старшите разряди на сумата. Настъпилата в този случай ситуация на антипрепълване не може да бъде отстранена в последния етап на алгоритъма при нормализация на мантисата на произведението. Нещо повече – тя може само да бъде засилена. Ето защо броячът на характеристиките се нулира, с което се осигурява стойност, съответстваща на p_min.

След записване на предварителната стойност на характеристиката на произведението в брояча на характеристиките входните регистри се изчистват така, че в тях остават само модулите на мантисите. Умножението им се извършва по модул по метода с младшите разряди напред по схемата с неподвижно множимо. Броят на циклическото повторение в алгоритъма се контролира от брояча на циклите БрЦ. Произведението като число с двойна дължина се разполага по дължината на РгY и редом стоящия РгИзм, който се освобождава от изместващия се надясно множител.

След получаване на произведението, същото при необходимост се нормализира, като се измества наляво през суматора с помощта на косата връзка към РгСМ. Компенсирането на порядъка при всяко изместване на мантисата се извършва в брояча на характеристиките БрН, който работи като реверсивен. Тъй като е възможна денормализация на мантисата на произведението само отдясно, то съдържанието на брояча на характеристиките БрН е възможно да бъде модифицирано единствено с изваждане на единици. Ако в частност е настъпил случаят с положително препълване (4-ти ред в таблица 3.3.5.2.2) и ако то е само на един порядък, то след евентуалната нормализация на мантисата това препълване се отнема и произведението става представимо число. В този смисъл в края на алгоритъма наличието на единица в k-тия бит на брояча на характеристиките БрН може да се приеме като признак за окончателно препълване при плаваща запетая:

Алгоритъмът на операция умножение завършва със сглобяване (запис) в РгСМ на елементите на резултата: мантиса, идваща от БуфРгY през суматора; характеристика от БрН и знак на произведението в РгСМ[n-1], според логическата функция неравнозначност от знаците на операндите, съхранени в тригерите на знаците.

3. Изпълнение на операция деление.

Алгоритъма за изпълнение на операция деление прилича в известна степен на този на операция умножение. В разглежданата структура, делимото Х се приема в РгX, а делителят Y в РгY. Изместващият регистър РгИзм се използува за формиране на частното Z=X/Y. След приемане на операндите, техните знаци се запомнят в тригерите TSx и TSy, а знаковите разряди на входните регистри се нулират. Така във входните регистри остават характеристиките и модулите на мантисите на операндите. Тези два елемента на числата се обработват поотделно – от характеристиките, като представители на порядъците, трябва да се получи разликата (p_x-p_y) и съответстващата й характеристика H_z, а мантисите трябва да се разделят. Тъй като логическата структура на устройството разполага само с един суматор, то обработката се извършва последователно.

Започва се с обработката на характеристиките – в участъка [n-1n-k-2] на буферния регистър БуфРгX се зарежда умаляемото – характеристиката на делимото H_x от РгX[Н]. Тъй като трябва да се изпълни операция изваждане (H_x-H_y), то в буферния регистър БуфРгY се зарежда инверсното съдържание на старшите (k+1) разряда на РгY, което ще представлява обратния код на умалителя – характеристика H_y. При подаване в суматора на допълващата единица +1[Н], на изхода му, в същия участък, се получава разликата: (S=H_x-H_y), която се записва в същия участък на РгСМ. Според определението за характеристиката (1.1.6.2.17) се получава числото:

която (според същото определение) е принципно невярна като характеристика на частното, тъй като й липсва отместването D. За да се получи необходимата характеристика, получената на изхода на суматора сума трябва да се коригира. Аналогично на операция умножение и тук поправката се постига апаратно, в процеса на пренасяне на получената сума от изхода на суматора до записването й в брояча на характеристиките БрН. Ще отбележим първо, че всички възможни ситуации при изваждане на порядъците, разгледани в пункт 3.3.3, сега трябва да се интерпретират в светлината на определението за изместен порядък и заедно с необходимостта от корекция на резултата (3.3.5.2.11). За целта k-разрядното поле на характеристиката, се разглежда на изхода на суматора съвместно със знаковия разряд, т.е. това е споменатият вече (k+1)-битов участък, заемащ разрядите от [n-1] до [n-k-2]. В този участък на разрядната мрежа се получава (k+1)-битова разлика от две k-битови числа без знак. От гледна точка на алгоритъма за деление на числа с плаваща запетая, в полето на порядъка са възможни същите 4 случая, описани за операция умножение:

1. Разликата S съответства на положителен порядък (p_z>0), получен без препълване

2. Разликата S съответства на отрицателен порядък (p_z<0), получен без препълване

3. Разликата S съответства на разлика от порядъци с положително препълване

4. Разликата S съответства на разлика от порядъци с отрицателно препълване

Въз основа на интервалните оценки за характеристиките (3.3.5.2.6) и (3.3.5.2.7) и тук при операция деление, както при операция умножение, ще анализираме четирите възможни случая.

Случай първи: (положителен порядък без препълване)

Изхождайки от вида на разликата (3.3.5.2.11), представляваща положителния порядък без препълване, то на изхода на суматора излиза резултат в следния общ вид:

който се характеризира с двете си старши нули.

Случай втори: (отрицателен порядък без препълване)

При условие, че приемаме разликата от характеристиките на изхода на суматора за отрицателно число, то следва че получаваме неговия допълнителен код. Модулът на този код за (k+1)-битовия участък има стойността

при което числото на изхода на суматора има следния общ вид:

Случай трети: (положително препълване в полето на порядъка)

Положително препълване в полето на порядъка може да се получи в случай, когато порядъкът на делимото е положителен, а този на делителят – отрицателен. Тогава при операция изваждане се стига до аритметическо събиране на модулите на порядъците, при изпълнение на което е възможно положително препълване за (k-1)-битовото поле на порядъка. Такова препълване се разпознава по преноса, възникнал от (k-2)-ия разряд. При това тълкуване резултатът на изхода на суматора има следния общ вид:

Случай четвърти: (отрицателно препълване в полето на порядъка)

Случай с отрицателно препълване настъпва, когато порядъкът на делимото е отрицателно число, а порядъка на делителя – положително. Тогава при операция изваждане се стига до аритметическо събиране на модулите на порядъците, чиято сума може да се получи с препълване. Като число тази сума е отрицателна, така че говорим за отрицателно препълване. Разликата обаче е възможна за (k+1)-битовия участък, където е представена в допълнителен код, а той има следния общ вид:

В крайна сметка изложените току що резултати, получени непосредствено след изваждане на характеристиките, могат да се обобщят и тълкуват според следващата таблица 3.3.5.2.3.

Таблица 3.3.5.2.3 Признаци на порядъка

V - препълване в полето на порядъка	СМ[n-1,n-2]	Разликата S съответства на	Признаци на операцията преди нормализация
0	0 0
1 (положително)	0 1		препълване при плаваща запетая
1 (отрицателно)	1 0		антипрепълване, което е възможно да отпадне
0	1 1

И така, получената разлика S е принципно невярна и следва да се поправи като към нея се прибави числото D. Освен това трябва да се отчете и стойността на самата сума, която е число без знак, което може да е получено с препълване и следователно е невярно. Това усложнява значително задачата за формиране на характеристиката. Не бива да забравяме, че в последния етап на алгоритъма (нормализация на резултата) е възможно да се наложи нейното допълнително модифициране, което може да се извърши само в брояча на характеристиките. Ето защо всички поправки, които ще се извършват върху получената сума следва да станат по пътя й от изхода на суматора СМ до входа на БрН.

Ще се спрем най-напред на случаите с препълване. Препълването в тези условия не може да се открие с помощта на функциите (1.2.3), (1.6.2.18) или (1.6.2.19), ето защо това се прави по данните в таблица 3.3.5.2.3. Така за препълването, което се фиксира в тригера ТП, се получава следната логическа функция:

Следва да се спрем на поправката на сумата. Добавянето на липсващото отместване - числото

може да се изрази така:

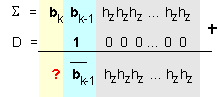
От горната рисунка се вижда:

1. Че младшите (k-1) разряда на разликата остават непроменени преминавайки в сумата, следователно те могат да се запишат в БрН директно.

2. Резултатът в разряд №(k-1) може да се получи чрез логическа инверсия на най-старшия бит на сумата.

Истинната стойност на знаковия бит на разликата, като предварителна стойност на характеристиката на частното, зависи от две неща:

· От това дали е открито препълване, т.е. какво е фиксирал тригерът ТП;

· И от получената в този бит стойност b_k.

Като се отчете необходимата стойност за да е в сила съответствието, което е представено в третата колонка на таблица 3.3.5.2.3, то истинната стойност, която трябва да се запише в k-тия разряд на БрН, се определя от следната логическа функция:

Веднага обръщаме внимание на факта, че тази функция напълно съвпада с аналогичната функция при операция умножение (3.3.5.2.9).

В резултат на всичко казано до момента, получената на изхода на суматора СМ разлика от двете характеристики, се записва в брояча на характеристиките БрН по шина, която извършва описаната метаморфоза, превръщайки я в предварителна стойност на характеристиката на частното. Шината има същата принципна логическа схема като синтезираната за операция умножение и показана на фигура 3.3.5.2.2. След записване на получената от суматора разлика в брояча на характеристиките с помощта на шината, представена на тази фигура, тълкуването на предварителната стойност на характеристиката на произведението е представено в следващата таблица 3.3.5.2.4

Таблица 3.3.5.2.4 Признаци на порядъка

Фиксирано в ТП препълване	СМ[n-1,n-2]	БрН[k,k-1]	Характеристиката съответства на	Признаци на операцията преди нормализация
0	0 0	0 1
1	0 1	1 0		препълване при плаваща запетая
1	1 0	1 1		антипрепълване, което е възможно да отпадне
0	1 1	0 0

Запис в БрН не се извършва единствено в случая на положително препълване. Последното може да се разпознае по комбинацията 01 в старшите разряди на суматора. Настъпилата в този случай ситуация на препълване не може да бъде отстранена в последния етап на алгоритъма при нормализация на мантисата на частното. Нещо повече – тя може само да бъде засилена, тъй като при евентуалната нормализация на мантисата към характеристиката трябва да се прибави още една единица.

След записване на предварителната стойност на характеристиката на частното в брояча на характеристиките входните регистри се изчистват така, че в тях остават само модулите на мантисите. Делението им се извършва по модул по метода без възстановяване на частичните остатъци, по схемата с неподвижен делител. Броят на циклическото повторение в алгоритъма се контролира от брояча на циклите БрЦ. Мантисата на частното се формира в РгИзм. Преди това обаче се проверява дали операцията е дефинирана. Ако делителят има нулева мантиса, операцията завършва с формиране на признака за "препълване при плаваща запетая".

След получаване на мантисата на частното, същата при необходимост се нормализира, като се измества надясно на един разряд през суматора с помощта на косата връзка към РгСМ. Компенсирането на порядъка при всяко изместване на мантисата се извършва в брояча на характеристиките БрН, който работи като реверсивен. Тъй като е възможна денормализация на мантисата на частното само отляво, то съдържанието на брояча на характеристиките БрН е възможно да бъде модифицирано единствено с прибавяне на единица. Ако в частност е настъпил случаят с отрицателно препълване (3-ти ред в таблица 3.3.5.2.4) и ако то е само на един порядък, то след евентуалната нормализация на мантисата това препълване се отнема и частното става представимо число. Ако това не се случи за резултат може да се приеме числото нула.

Преди да се сглоби крайният резултат, се проверява дали не са настъпили или не са изчезнали препълванията в полето на порядъка, като се формират окончателно признаците на резултата.

Алгоритъмът на операция деление завършва със сглобяване (запис) в РгСМ на елементите на резултата: мантиса, идваща от РгИзм през суматора; характеристика от БрН и знак на частното в РгСМ[n-1], според логическата функция неравнозначност от знаците на операндите, съхранени в тригерите на знаците.

Следващият раздел е:

3.3.5.3 Модулно-логаритмична аритметика ( Modular-Logarithmic Processor )