3.3.5.3 Модулно-логаритмична аритметика
Modular-Logarithmic Processor
Уважаеми
Читателю, в научната и в учебната литература емоциите на авторите като правило
са забранени или ако не са забранени, то те се приемат за излишни. Ние обаче,
тук в началото на този раздел, няма да се въздържаме. Този раздел е нов и
въпреки, че някой може да ни упрекне, не искаме да спестим вълнението, което ни
обхваща, наблюдавайки развитието на любимата ни научна област. Аз съм вече в
края на своя творчески живот и за сетен път се убеждавам, че след моето
поколение идват нови и нови поколения, които използват, преосмислят и творят
върху на пръв поглед “изчерпани” теми. Сега е 2017 година! Имайки предвид
изложеното до тук, някой може да остане с впечатлението, че вече няма какво да
се добави и че съвършенството е постигнато! Но ето че се появява някой и
разбива това впечатление. Това ни води до извода, че съвършенството е
непостижимо, но стремежът към него е вечен!
В началото на 2017-та година се появи следната статия
http://www.tyanev.com/resources/docs/5989-14302-1-PB.pdf
Представената в нея реализация ни задължава да запознаем читателя със същността й, което ще се опитаме да направим тук възможно по-подробно, за да го подпомогнем. В самото начало не можем да избегнем представянето на числата, което се основава на достатъчно сложно математическо обосноваване. Това няма да успеем да направим със степента на детайлност, която бихме желали, но все пак следва да поясним на какво се основава реализирания иновативен хардуер. Запознавайки се с подтемите, които ще следват по-долу, читателят вероятно ще разбере защо тези методи за представяне и обработване на числата бяха умишлено пропуснати в началната глава на тази книга. Тук обаче обстоятелствата ни задължават да говорим за това, още повече, че заедно с цитираната по-горе разработка има и други подобни. Това е поредното доказателство, че читателят ще трябва да поддържа, доколкото това му е възможно, своята компетентност с постоянни усилия.
1.
Теоретико-числова основа за създаване на бройни системи с остатъчни
класове
Четни и нечетни цели числа. Деление на 2.
Всеки знае, че числата могат да се
определят като четни или като нечетни. Четните са тези, които се делят на
числото 2 без остатък, т.е. остатъкът е нула. Нечетни са тези числа, които не
могат да се разделят на две равни части – едната винаги съдържа една единица в
повече. Или ако бъдат отделени две еднакви части, винаги отделно остава още една
единица, т.е. остатъкът е единица. Така едно четно число може да се изрази с
двете си еднакви половини чрез произведението (2.р). По този начин нечетното
число може да се изрази така (2.р+1).
Не е сложно да се провери, че сумата от две четни, както и от две нечетни числа, е четно число, а сумата от четно и нечетно е нечетно число:
Таблица за събиране и умножение по модул 2
|
+ |
Ч |
НЧ |
|
x |
Ч |
НЧ |
|
Ч |
Ч |
НЧ |
|
Ч |
Ч |
Ч |
|
НЧ |
НЧ |
Ч |
|
НЧ |
Ч |
НЧ |
Например, че произведението на две нечетни числа, е нечетно число:
(2.p+1)x(2.d+1) = 4.p.d+2.p+2.d+1 = 2.(2pd+p+d)+1 .
Деление на 3. Остатъци.
В
този случай възможните остатъци са три – 0, 1, 2. Делящите се точно числа могат
да се представят чрез произведението (3.k), но неделящите се са два вида и се
представят съответно чрез изразите (3.k+1)
или (3.k+2). В
съответствие на тези изрази могат да се формират аналогични на горните таблици
за операциите събиране и умножение, имащи вида:
Таблица за събиране и умножение по модул 3
|
+ |
0 |
1 |
2 |
|
х |
0 |
1 |
2 |
|
0 |
0 |
1 |
2 |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
2 |
0 |
|
1 |
0 |
1 |
2 |
|
2 |
2 |
0 |
1 |
|
2 |
0 |
2 |
1 |
Формулирана и доказана е теорема, според която: делението на
две цели числа с остатък е винаги възможно, при това по един единствен начин.
В стила на горните изводи могат да бъдат разгледани и други
модули.
Сравнение по модул.
Основните
понятия, които ще споменем тук, вече бяха въведени и определени в началото на раздел 1.6.2 от глава 1 на тази книга. Въпреки това,
тук ще повторим основните положения на теорията, за да бъдем верни на горното
заглавие и за да го представим по-пълно.
Избираме натурално число М (положителна
константа). Разглеждаме това число като делител на различни цели числа Xk ; k=0,1,2,3,4, … ,
при което се интересуваме от получаваните остатъци Rk . Анализът
на получаваните цели остатъци води до няколко интересни извода:
1. Възможните
остатъци са положителни числа, които принадлежат на затворения интервал
[
0, (M-1)
].
С други думи, безкрайното множество от числа Х поражда
крайното множество на възможните остатъци. Тези остатъци са числата
0, 1, 2, 3, 4, ... (М-2),
(М-1) ;
2. На
всяка стойност Rk съответства едно единствено
безкрайно множество (клас) от числа Х, които са в смисъла на числото М;
3. Тези
М на брой безкрайни множества са непресичащи се.
В крайна сметка се въвежда
следното определение:
Две числа Х1 и Х2 са сравними по модул М тогава и само тогава, когато при делението им с числото М, се получават еднакви остатъци, което се записва така
![]()
или още
така:
![]()
Пример:
Нека Х1=69 и Х2=363. Нека модулът, по който ще ги сравняваме, е М=7.
Тогава Rx1=R(69/7)=6, Rx2=R(363/7)=6. Тъй като остатъците са еднакви Rx1=Rx2 , заключаваме, че
![]()
Може да се изкаже еквивалентно определение:
Две числа Х1 и Х2 са сравними по модул М, ако разликата (Х1-Х2) се дели на М.
С други думи, ако тези две числа се делят
на М с еднакъв остатък R, това
може да се изрази така:
X1 = M.s1 + R,
X2 = M.s2 + R,
при което
разликата им се изразява така:
X1 - X2 = M.s1 – M.s2 = M.(s1-s2) .
Вижда
се, че полученото число се дели без остатък на М, което подкрепя горното
определение.
Сравнението на две числа, декларирано чрез
(3.3.5.3.1), има следните основни свойства:
1.
Отношението е рефлексивно, т.е.
![]()
2.
Отношението е симетрично, т.е.
![]()
3.
Отношението е транзитивно, т.е.
![]()
4.
Ако числа Х1 и Х2 са сравними по модул М, и ако q е произволно цяло число,
![]()
5.
Ако
![]()
![]()
6.
Ако
![]()
7.
Ако q е произволно натурално число и
ако
![]()
8.
Ако q и М са произволни натурални числа, и ако
![]()
9.
Ако
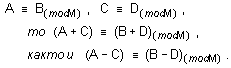
10.
Ако
![]()
11.
Ако
![]()
12.
Ако
![]()
е произволен многочлен с
цели коефициенти, то
![]()
13.
Всяко събираемо от лявата или от дясната част на
сравнението може да бъде прехвърлено в противоположната част с противоположен
знак.
14.
![]()
Горните
свойства не изчерпват математическите функционалности в теоретико-числовата
основа на разглежданата област. Читателят следва да разбира, че пропуските,
които ние тук ще направим, са умишлени. Това се налага, за да не се
отдалечаваме съществено от крайната си цел Ще споменем обаче още някои
функционалности и твърдения, които са неразделна част от същността на
изложението.
Съществува
теорема за деление с остатък и алгоритъм за изчисление (алгоритъм на Евклид).
Твърди се, че да се раздели число А на число В (В≠0) с остатък, означава,
да се намери двойка цели числа s и R, които изпълняват условията
A = B.s + R
, 0 ≤ R <
B ,
(3.3.5.3.3)
където с R е означено цяло число, наричано остатък, а с s е
означено цяло число, наричано частно.
В светлината на горе изложеното, делителят B може да
се определи като модул за сравнение (аналог
на М). Числото s в раздел 1.6.2 на тази книга беше наречено коефициент на
кратност на модула M. В
смисъла на тази интерпретация можем да запишем твърдението така
М ≡ B , A = М.s + R , 0
≤ R <
M .
(3.3.5.3.4)
Съществува теорема, определяща броя на
деленията, както и теорема, определяща броя на цифрите в резултатите.
Изследвайки кратко представените
определения и зависимости, както беше посочено в глава 1, не е сложно да
възникне идеята за използване на съответствието между числото и неговия остатък
(в смисъла на конкретния модул) като своеобразен начин за кодиране, в
съответствие с определението за кодиране, дадено в началото на раздел 1.1. Така остатъкът Rx може да се определи като
изображение на числото, т.е. може да се запише
![]()
Тук за изразяване на изображението е използвано условното означение, което беше определено в тази книга и многократно е употребявано във всички наши книги. Във връзка с числото Х и неговото изображение [Х] са известни две задачи:
· Права задача – при дадено Х, да се намери неговото изображение [Х];
· Обратна задача – при дадено изображение [Х], да се намери числото X.
Както
беше пояснено в § 1.1 на
тази книга, кодът трябва да обезпечава единствено решение както за правата
задача, така и за обратната задача. В смисъла на въведеното тук сравнение по
модул обаче, обратната задача няма единствено решение, а безкрайно много
такива, което е изразено чрез коефициента на кратност s, в (3.3.5.3.5). По тази причина изображението [X] не бихме могли да наричаме код на
числото X.
Като прелюдия към следващите
функционалности, които следва да представим, ще разгледаме следната обратна
задача.
Задача:
Известна е системата от изображения:
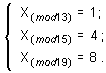
Необходимо
е да се определи числото Х.
Общи
забележки към задачата:
Ще
припомним, че множеството от числа, които по модул 13 генерират изображението
1, е безкрайно. Същото се отнася за останалите два модула. В този общ случай,
да се намери като елемент в тези множества, едно и също число Х,
удовлетворяващо горната система в общия смисъл, е малко вероятно.
От елементарни съображения за делимост
обаче, в съответствие с дефиницията за сравнимост по даден модул, едно
необходимо, а оказва се и достатъчно условие, за да имат подобен вид системи
решение, е най-големият общ делител (НгОД) на всяка двойка модули да дели точно
разликата от числата в десните страни на сравненията по тези модули (вижте по-горе 9-то свойство). При
тези условия решението ще бъде единствено
множество (единствен клас) от числа сравними по този модул, което е най-малкото
общо кратно (НмОК) от модулите на системата.
Числото 13 се дели на 1 и на 13. Числото 15 се дели на 1,
на 3, на 5 и на 15. Следователно, според горното твърдение, НгОД на тези две
числа е 1. Това отговаря на определението за взаимна простота или с други думи
13 и 15 са взаимно прости числа, тъй като техният НгОД е числото 1. Това
свойство се отнася и за останалите възможни двойки в примера (13 и 19) и за (15
и 19).
Доказано е, че при такава ситуация подобни системи винаги
ще имат единствено решение (независимо
от числата в десните страни на сравненията). Това решение определя клас от числа с еднакви остатъци
при деление с числото 13*15*19=3705, т.е. това е клас (множество от числа),
който се формира от (съответства на) модул 3705.
Решение: Решението на нашата конкретната
система, намираме последователно така.
Представяме неизвестното число чрез остатъка и модула от първото уравнение на системата:
![]()
където с t е
означено съответното на модула 13 неизвестно частно.
Заместваме числото Х във второто уравнение на системата с
получения израз
![]()
което,
въз основа на по-горе изложените свойства, може да се запише както следва
![]()
За да решим уравнението с неизвестно
числото t, можем да
забележим, че НгОД на константите в него, 3 и 15, е числото 3, т.е. 3=(3,15), а
това ще означава, че числото 3 трябва да дели произведението
13.t .
Забелязваме още, че числата
3 и 13 са взаимно прости, което пък означава, че
![]()
Като заменим така получения за параметъра t
израз в уравнение за третото сравнение, ще получим
![]()
а след деление на 3, горното уравнение добива вида
![]()
по силата на 8-мо свойство, записано по-горе.
Според второто определение за сравнимост,
дадено по-горе, всяко число Y, което
по модул 5 е сравнимо с числото 1,
може да се изрази така: Y=5.s+1. Едно число в този клас е числото 5.1+1=6, с което заменяме
числото 1 в дясната част на последното сравнение, т.е.
![]()
Сега (според 9-то свойство) можем да
заменим числото 13 в лявата страна на разглежданото сравнение с неговия остатък
3, който се получава при делението му с модула 5. Така сравнението добива нов
вид
![]()
Разделяме двете страни на това сравнение с
числото 3 и получаваме
![]()
което ни
позволява да изразим класа на числото s чрез
някое цяло число k така: s=5.k+2.
Сега за неизвестното t
можем да запишем
t =
3.s = 3(5.k+2) = 15.k+6 ,
и тогава системата от първите две уравнение
ще има решението
X =
13.t + 1 = 13(15.k+6) + 1 = 195.k + 79.
Тъй като търсеното решение X трябва да удовлетворява и
последното трето сравнение в дадената система, след заместване на горе
получения израз за X в него,
получаваме
![]()
След деление с числото 19, за лявата част
получаваме остатъците 5 и 3, а сравнението приема вида
![]()
резултат,
който се основава на 9-то свойство.
В крайна сметка след прехвърляне на
остатъка 3 в дясната част, се достига до крайния вид
![]()
След деление на 5 получаваме решението
![]()
Последното означава, че k
принадлежи на класа k=19.h+1, за някое цяло число h.
Заместваме това решение за k в
решението за X
X =
195(19.h+1) + 79 = 3705.h + 274 .
Следователно решението на
изходната система е класът от числа
(3705.h+274).
Модулът на това решение е
числото 3705, което, забележете, е произведението 13.15.19 = 3705 !
Ако се ограничим и отхвърлим възможността
за кратност на модула в решението (т.е. приемем, че h=0), тогава
решението на изходната система е Х=274.
Използваме
представения току що пример, за да обърнем внимание на възможността едно число X да се представя чрез своите
изображения в смисъла на няколко различни модула, които в горния пример
определят дадената система от три уравнения.
Изображението на едно число, в
смисъла на няколко модула за сравнение, се представя като кортеж от
изображенията на числото по всеки отделен модул
![]()
Това ни дава право да представим търсеното в горния пример число, според определението (3.3.5.3.6), така
![]()
И още една функционалност - модулът M на изображението, определено чрез (3.3.5.3.6), е произведението
![]()
Възниква естественият въпрос: каква е
ползата от този начин на представяне на числото?
Все още не сме готови да отговорим пълно на този въпрос, тъй като изложението не е завършено, но дотолкова, доколкото вече дадохме определение, тук ще изтъкнем, че колкото по-дълъг е кортежът (3.3.5.3.6), толкова по-голям е диапазонът на представимите по този начин числа, което е в пълно съответствие с определението (3.3.5.3.5).
2.
Китайска теорема за остатъците и нейната ролята при представянето на
числата в бройни системи с остатъчни класове
В основата
на многомодулното представяне на числата (3.3.5.3.6) стои така наречената “Китайска
теорема за остатъците”. За първи път тази теорема е спомената в един
трактат на китайския математик Сун Цзи, някъде през 3-ти век преди Н.Е. Тя
позволява да се определи едно цяло число, ако са известни неговите остатъци по
няколко прости модула. Нейното твърдение е следното:
Теорема: Ако са известни k на брой
числа p1, p2, p3, … , pk, всяко от които е по-голямо от 1,
и във всяка
образувана двойка от които,
числата са взаимно прости, то съществува единствено неотрицателно решение по
модул P=p1.p2.p3. … pk на следната система от сравнения:
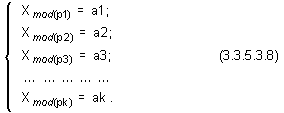
С други думи, кортежът
( a1, a2,
a3, … , ak ) = [X] (3.3.5.3.9)
представлява
изображение на всяко цяло число X,
намиращо се в интервала [ 0 , (P-1) ], при което
X
≡ aj (modpj) , j = 1,2,3,…,k ,
или още
![]()
Следва
да поясним, че единственото число X,
което се намира в указания интервал [ 0
, (P-1) ], е числото с коефициент на кратност s=0 (вижте (3.3.5.3.3)). В горния израз всъщност
отношението
![]()
представлява
цяло число – частно от делението на X с
модула pj, което
частно нарекохме още коефициент на кратност s, т.е. число, което показва колко пъти модулът се съдържа в
числото X. При
неточно деление, записаната по-горе в израза разлика, позволява да се определи
остатъка от делението, числото aj.
Теоретично числата, които могат да имат
същото изображение [X], са
безкрайно много. За техническата реализация на този вид представяне на числата
обаче единствеността е безусловно изискване.
Окончателно вече трябва да изтъкнем, че представянето (изобразяването) на целите числа чрез кортеж (наредена последователност) от вида (3.3.5.3.9), по силата на определени и предварително приети предпоставки, се нарича СОК (бройна система в остатъчни класове). Кортежът (3.3.5.3.9) се нарича код на числото, неговите елементи aj се наричат цифри, а числото k се нарича дължина на кода.
Всяко
представяне на числа от представимия диапазон, е само съставен елемент на
съответната машинна аритметика и не може да се разглежда отделно от нея.
Аритметическите свойства на една или друга бройна система се определя преди
всичко от характера на междуразрядните връзки, които се появяват по време на
изпълнение на операции между кодовите думи. Ако читателят е запознат с предходното
съдържание на тази книга, както и с началните раздели на книга [2],
следва да се е убедил в това, че в рамките на обикновените позиционни бройни
системи, значително ускоряване на аритметическите операции не е възможно да
бъде постигнато. Това се обяснява с това, че стойността на всеки отделен
разряд, освен на най-младшия, представляващ резултат на някаква двуместна
аритметическа операция, зависи не само от стойността на цифрите в текущия
разряд, но и от всички по-младши от нея разряди. Това означава, че позиционните
бройни системи имат строго последователна структура. Съвременните изчислителни
системи обаче определено предпочитат онези изчислителни структури, които
притежават способност към паралелна обработка на данните. Такива способности
притежават непозиционните кодови системи,
позволяващи реализация на идеята за разпаралелване на операциите на нивото на
аритметическите операции. Идеята за описаното изобразяване на числата е описана
за първи път в серия публикации на чешките учени М. Валах (M. Valach) и
А. Свобода (A. Svoboda) в периода 1955-1957 година.
Описаната
по-горе система за представяне на числата (СОК) се определя като непозиционна.
И като такава всички рационални операции между две числа, представени в нея,
могат да се изпълняват паралелно между отделните цифри във всички разряди.
Поради отсъствие на междуразрядни връзки при изпълнение на операциите това
естествено води до повишаване на бързодействието им. Този силен ефект обаче е
придружен от някои присъщи на тази система недостатъци, като например:
·
Ограниченост на действията само върху множеството на
положителните цели числа;
·
Затруднено сравнение на числата по стойност;
·
Затруднено откриване на препълването (излизане на
резултата от представимия диапазон).
Ето защо за ефективно преодоляване на тези недостатъци
са провеждани сериозни научни изследвания, дълбочината на които
ние тук е невъзможно да постигнем. Разчитаме на добрата воля на читателя и на
неговата любознателност.
Този раздел е в процес на разработка
и още не е завършен
Следващият
раздел е:
§ 3.4 Операции върху
двоично-десетични числа ( Operations
with binary-decimal numbers )