3.4.3
Операция
умножение на
2/10-чни числа
Multiplication
Умножение
на числа в 2/10-на
бройна
система може
да се изпълни
както по
метода с
младшите разряди
напред, така
и по метода
със старшите
разряди
напред. В
случай, че
съмножителите
са
представени
в прав код,
умножението
се извършва
по модул, а
знакът на
произведението
се определя чрез
логическата
функция
неравнозначност.
В този случай
тук интерес
представлява
процесът на
получаване
на
поразрядното
произведение
![]()
За
разлика от двоичната
бройна
система,
поразрядното
произведение
в случая може
да има десет
стойности, от
(X.0) до (Х.9).
Свързаната с
това
произведение
операция
умножение, не
може да бъде
редуцирана
до по-елементарни
операции,
което
означава, че
тя следва да
бъде изпълнявана
фактически.
В
повечето
алгоритми и
логически
структури
всяко
поразрядно
произведение
се изчислява
според
определението
за операция умножение,
т.е. чрез
многократно
натрупване на
множимото Х,
например
Х.3=0+Х+Х+Х. За
целта
поредната
цифра на
множителя yi се
зарежда в
изваждащ
брояч, в
качеството й
на негова
начална
стойност,
след което
започва
циклическо
натрупване
на множимото Х към
междинната
сума без
измествания.
Натрупването
продължава
докато се
нулира
изваждащият
брояч. Едва
след това се
извършва
изместване
на един
десетичен
разряд на множителя
и на
междинната
сума (или на
множимото).
Тук може да
се направи
извода, че
фактическото
натрупване
на текущото
поразрядно
произведение
може да
отнеме доста
време (до 9
операции
събиране).
Изказаният
алгоритъм е
неефективен
за апаратна
реализация. В
чист вид той
най-често се
програмира.
Ускоряване
на
умножението
може да се
постигне
чрез
ускоряване
на
натрупването
на поразрядното
произведение.
Последното
може да бъде
постигнато
например,
чрез предварително
получаване и
едновременно
съхранение
заедно с
множимото и
на неговите
кратни: (2.Х) и (4.Х).
Те могат да
бъдат
получени още
със зареждането
на
операндите в
логическата
структура на
устройството
за умножение.
Използването
на тези
стойности
става в
процеса на
умножение по
следния
начин: ако
десетичната
тетрада на
поредната
цифра от
множителя се
разгледа
като двоично
число (за
цифрите на
числото се
има предвид
кода “8421”):
![]()
последното може да се представи така:
![]()
т.е. ако например yi=9=1001,
тогава 9 =
2.(100) + 1.
Тази
интерпретация
на цифрата yi, във
връзка с
умножението (X.yi), ще има
следния
ефект:
![]()
където В
представлява
числото,
което е
еквивалент на
старшите три
бита на
тетрадата,
т.е.
![]() .
.
Тъй
като
произведението
2.Х е на
разположение
винаги,
същото се
натрупва B пъти и
в случай, че
тетрадата е
нечетна (т.е. b0=1), се
прибавя още
един път
множимото Х. По
този начин
максималният
брой
натрупвания,
съответствуващи
на цифрата 9 се
намалява на 5.
Аналогичен
е подходът,
когато се
разполага
допълнително
и с
учетвореното
множимо. Тогава
9=4+4+1 и
събиранията
са максимум три.
Натрупването
на
поразрядното
произведение
по този начин
все е още твърде
бавно, затова
често се
прилага табличното
умножение.
Табличното
умножение
изисква работа
с отделните
десетични
цифри xi на
множимото X:
![]()
където (xj.yi) се
нарича поцифрено
произведение. Тогава
поразрядното
произведение
(X.yi) може
да се
представи
като сума от
поцифрените
произведения
в следната
схема:
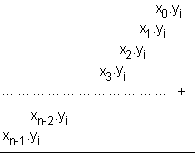
Следователно
поразрядното
произведение
е сума от
поцифрените
произведения,
които могат
да се вземат
наготово от
таблицата за
умножение,
запомнена в
постоянно
запомнящо
устройство.
Тъй като
поцифрените
произведения
са двуцифрени
числа
(например 8.7=56), то
запомнящото
устройство
се разделя на
два блока - за
младшите и за
старшите
цифри на
поцифрените
произведения,
както е
показано в
таблица 3.4.3.1.
Разполагайки
с готовите
поцифрени
произведения,
може да се
формулира
следния
алгоритъм за
изчисляване
на
поразрядното
произведение.
Използувайки
цифрите на
текущото
поцифрено
произведение
(xj.yi) в
качеството
на адреси, от
блока на
младшите и
блока на
старшите
цифри на
таблицата могат
да бъдат
извлечени и
формирани
две отделни
последователности
-
последователност
от младшите
цифри на поцифрените
произведения:
![]()
и
последователност
от старшите
цифри на поцифрените
произведения
![]()
Таблица
3.4.1.1
Десетичните
поцифрени произведения
|
(SH) Старши
цифри |
|
(SL) Младши
цифри |
||||||||||||||||||||
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
2 |
0 |
2 |
4 |
6 |
8 |
0 |
2 |
4 |
6 |
8 |
|
3 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
2 |
2 |
2 |
|
3 |
0 |
3 |
6 |
9 |
2 |
5 |
8 |
1 |
4 |
7 |
|
4 |
0 |
0 |
0 |
1 |
1 |
2 |
2 |
2 |
3 |
3 |
|
4 |
0 |
4 |
8 |
2 |
6 |
0 |
4 |
8 |
2 |
6 |
|
5 |
0 |
0 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
|
5 |
0 |
5 |
0 |
5 |
0 |
5 |
0 |
5 |
0 |
5 |
|
6 |
0 |
0 |
1 |
1 |
2 |
3 |
3 |
4 |
4 |
5 |
|
6 |
0 |
6 |
2 |
8 |
4 |
0 |
6 |
2 |
8 |
4 |
|
7 |
0 |
0 |
1 |
2 |
2 |
3 |
4 |
4 |
5 |
6 |
|
7 |
0 |
7 |
4 |
1 |
8 |
5 |
2 |
9 |
6 |
3 |
|
8 |
0 |
0 |
1 |
2 |
3 |
4 |
4 |
5 |
6 |
7 |
|
8 |
0 |
8 |
6 |
4 |
2 |
0 |
8 |
6 |
4 |
2 |
|
9 |
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
9 |
0 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
8.7 =
56
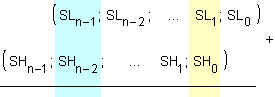
Сумата
на тези две
последователности,
изместени
една спрямо
друга на един
десетичен
разряд,
представлява
поразрядното
произведение
(X.yi) :
Натрупването
на
поразрядното
произведение
в междинната
сума обаче
може да стане
в един
суматор. Това
изисква
последователностите
SL и SH да се
събират
непосредствено
и последователно
с междинната
сума. За
целта
текущата цифра
yi на
множителя се
комбинира последователно
с
всяка цифра
на множимото,
като при това
се подготвя
във входния
регистър
последователността
от младши
цифри на
поцифрените
произведения
SL.
Формираната
последователност
се прибавя
към
междинната
сума и
входният
регистър се
освобождава.
В него, след повторно
последователно
комбиниране
на текущата цифра
yi на
множителя с
всяка цифра
на множимото,
се формира
последователността
от старши
цифри SH,
след което тя
също се
прибавя към
междувременно
изместилата
се на един
разряд междинна
сума, както е
показано на
горната
рисунка. С
тези
микрооперации
завършва
текущият
такт на
умножението.
След
изместване
на множителя,
действията,
описани
по-горе, се
повтарят.
За
да може да се
реализира
този
алгоритъм регистърът,
който ще
съдържа
множимото,
трябва да
осъществява
циклическо
изместване.
Входният
регистър,
който ще
подава към суматора
последователностите
SH и SL, трябва
също да бъде
изместващ.
Синтезът на
логическа
структура за
операция
умножение
оставяме на
читателя.
По
същество иизложихме
кратко три
алгоритъма
за умножение.
Вероятно
читателят е
забелязал, че
тук ние не
представяме
логическа
структура на
устройства,
реализиращи
описаните
алгоритми. По
тази причина
не са
представени
и
микропрограмите
на тези
алгоритми. С
това целим да
провокираме
читателя,
щото той сам
да довърши
необходимото.
Нашето
разбиране по
този въпрос
се изразява в
следното -
започвайки
изложението
на операционните
устройства в
началото на
трета глава достатъчно
подробно, да
достигнем
тук до това
кратко
изложение и
разчитайки
на
подготовката,
която читателят
вече е
постигнал, да
сме уверени,
че той ще
бъде в състояние
да ни разбере
и при
необходимост
да направи
необходимото
за синтез и
реализация на
необходимата
му логическа
структура. Разбира
се, излагайки
възможните
алгоритми,
ние сме
предложили и
коментирали
до голяма
степен
необходимите
логически
възли за една
такава
бъдеща
структура.
Следващият
раздел е:
3.4.4
Операция
деление ( Division
)