Този раздел е нов. Създаден е през 2021 година.

3.4.5 Смесена десетично-двоична форма на числата
с плаваща запетая - (СДДФ) , (С10/2Ф)

Decimal-Binary floating point form of numbers (DBFPF)

Двоични изчисления за десетична аритметика

Удобната и най-използвана система за изчисления е десетичната. В редица ситуации обаче възниква въпросът за точността на получаваните резултати. И тъй като в съвременни условия изчисленията са предимно машинни, а машините, които ги изпълняват, използват двоична бройна система, то възниква въпросът за точността на десетичните резултати, получавани чрез средствата на двоичната аритметика. По-долу ще поясним ползата от обработка на реални десетични числа, представени във форма с плаваща запетая, постигащи точността на ръчното изчисление. Тази обработка се основава на алгоритми, в които се използва двоична аритметика, регламентирана от стандарта IEEE-754.

И така, освен десетичната, съществуват различни q-ични бройни системи, за които ние подробно писахме в глава 1 на тази книга, така също в много други нейни раздели. За представяне на числата са изобретени две системи – естествена и мултипликативна, които ние също подробно сме пояснили. Ще припомним само, че за мащабирането на числата, което се налага като по-удобно за някои много малки или много големи числа, се прилага преди всичко мултипликативната форма, която още се нарича форма с плаваща запетая (ФПЗ). В случаите, когато порядъкът на числото е нула, то най-удобно се представя в естествен вид, който наричаме форма с фиксирана запетая (ФФЗ).

Ние се задължаваме да представяме числата с максимална точност, особено когато става дума за числата плаваща запетая. Това се изразява в понятието нормализирана мантиса. За съжаление точността за представяне на числата в технически формат зависи изключително от дължината на полето, в което се записва значещата част на числото. Техническият формат обаче във всички случаи има ограничена дължината, което е основният източник за загуба на част от значещата част на числото, с други думи на точността за представянето му.

По своята физическа природа числата се представят с приближение. Това се дължи на несъвършенството на създадените от човека измервателни инструменти. По тази причина говорим за изчисления и резултати, които следва да удовлетворяват зададената от потребителя точност. За точността на резултата или още за грешките, с които той се получава, читателят следва да се обърне още към изложеното в раздел 3.3.4 на тази книга.

Тъй като десетичната и двоичната бройни системи са несъизмерими, то при преобразуване на реалните десетични числа в двоични обикновено се получава приблизителен еквивалент, който възпроизведен обратно не съвпада с изходното число. Това е свързано с правилото за закръгляне – еквивалентната стойност може да е по-малка или по-голяма спрямо изходното число. Единственият начин да се намалят тези грешки е удължаване на разрядната мрежа.

Числата, получени с приближение могат да съдържат верни, съмнителни и неверни цифри. Неверните цифри влияят на точността на изчисленията и не рядко водят към съвършено неправилни резултати. Неверните цифри се стараем да избегнем чрез някоя от четирите схеми за закръгляне. Простото отхвърляне на излишните двоични цифри в двоичното число с цел закръгляне на десетичния еквивалент до желания брой десетични цифри, най-вероятно ще породи неверни цифри в последния.

Всяко реално число, представляващо правилна дроб, може да бъде представено във ФПЗ, в която мантисата е цяло число.

Ако числото е представено във ФПЗ с целочислена мантиса, то мантисата и порядъкът на това число могат да се преобразуват в двоична бройна система точно.

Смесена десетично-двоична форма на числата

Въвеждаме нова форма за представяне на числата (СДДФ), както е обявено в заглавието. В този формат мантисата на десетичното число с плаваща запетая е представена с точност от m на брой десетични цифри. При това се приема, че мантисата е цяло ляво подравнено число със знак. Порядъкът е също цяло число със знак. Числа, записани по тези правила ще се наричат нормализирани и съответстват на формулата

където s означава знак. И в двата случая знакът е кодиран с двоични цифри както обикновено:

Следва да помним, че основата на числата в този формат е числото q=10.

Мантисата се записва в поле с дължина m разряда, а порядъкът p в поле с дължина k разряда. Такова изображение на десетичното число се нарича нормализирано. Например, при m=7 и k=4, последователността

0 1234560 1 0004

ще се чете като десетично число в мултипликативен вид съответно

+1234560.10^-4 ,

чиито естествен вид е числото +123,4560.

Минималната стойност на нормализираната десетична мантиса в горната примерна структура е цялото число 1000000, а максималната е цялото число 9999999.

Предложената форма се нарича смесена, защото мантисата и порядъкът не могат да се представят машинно непосредствено, а се представят чрез своите двоични еквиваленти.

В смесената десетично-двоична форма (СДДФ) десетичните числа се представят според следната структура

,

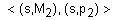в която мантисата М и порядъкът р имат свои собствени знаци s.

В тази структура мантисата М е представена в поле с дължина i бита, като ляво подравнено цяло двоично число със знак, а порядъкът в поле с дължина j бита, като цяло двоично число със знак. Така (i+j)=n е общата двоична дължина на разрядната мрежа.

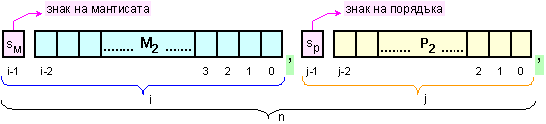
Фиг. 3.4.5.1. Структура на разрядна мрежа с плаваща запетая в СДДФ

Ако в една 32 битова разрядна мрежа (n=32=i+j, i=25, j=7), 24 бита се отделят за модула на мантисата, един разряд за знака на числото, още един за знака на порядъка, и тогава останалите 6 бита могат да съдържат модула на порядъка. Максималната стойност от шест двоични единици в полето на порядъка съответстват на десетичната стойност 63. Така модулът на представяните в тази примерна СДДФ десетични числа ще се намира в интервала

т.е.

В същото време припомняме, че формулата за двоичния вид на числото в стандарта IEEE-754 във форма с плаваща запетая има вида

Така за двоичния еквивалент на максималната мантиса 9999999 е необходимо поле с дължина i=24[b]:

99999999₍₁₀₎ = 100110001001011001111111₍₂₎ .

Изчисления в смесена десетично-двоична форма на числата

Аритметичните операции между десетичните числа с плаваща запетая се изпълняват обикновено, в които всички аргументи са цели числа.

Резултатът от всяка аритметична операция следва да бъде нормализирана според указаното по-горе правило и закръглена до най-близката цяла стойност. Тъй като порядъкът съответства на десетичната основа на бройната система, нормализацията на резултата изисква той да бъде умножен или разделен на 10 (1010). Броят на десетичните цифри в нормализираната двоична мантиса трябва да бъдат не повече от m.

Ще илюстрираме аритметичните операции между числа, представени в тази форма със следния пример: да се изчисли резултатът от израза с точност до m=7 цифри:

Ръчното изчисление, както и това с калкулатора на Windows, довежда до стойността 8,000000 .

И така, нека запишем операндите с нормализирана мантиса:

Във въведената за представяне структура, тези десетични операнди ще бъдат се записват така:

A = [ 0, 9675423, 1, 1 ] = [ 0, 100100111010001010011111, 1, 000001 ] ;

B = [ 0, 9675421, 1, 1 ] = [ 0, 100100111010001010011101, 1, 000001 ] ;

C = [ 0, 1000000, 0, 0 ] = [ 0, 000011110100001001000000, 0, 000000 ] ;

D = [ 0, 1999920, 1, 1 ] = [ 0, 000111101000010000110000, 1, 000001 ] .

Намираме разликата от мантисите MS=MA-MB. Тъй като порядъците на числата са еднакви (-1), изпълняваме изваждането

MS = 9675423 – 9675421 = 2 ;

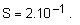
В новата форма резултатът за S следва да бъде записан така

S = [ 0, 2000000, 1, 7 ] = [ 0, 000111101000010010000000, 1, 000111 ] .

Ще изчислим произведението P=S.C. Според математическите правила трябва да умножим мантисите и да съберем порядъците на двата операнда.

Полученото произведение следва да нормализираме:

P = [ 0, 2000000, 1, 1 ] = [ 0, 000111101000010010000000, 1, 000001 ] .

Последното действие е изваждане R=P-D.

За сравнение, изчисляваме стойността на същия израз с помощта на Excel. Получаваме следния резултат:

Фиг. 3.4.5.2. Резултат от изчисление на примерния израз в Excel

Както може да се види, резултатът не е точен и не съвпада с изчисления ръчно. Подобна неточност в резултата се получава от всяко приложение, създадено с известните програмни средства, в които се използва двоично представяне на операндите в израза според стандарта IEEE 754. Причините за това бяха подробно изложени в преходния раздел 3.3.4 на тази книга. За грешките от двоичните изчисления се говори и много други раздели, когато е имало повод, с което сме искали непрекъснато да държим потребителя (програмиста) свързан с особеностите на хардуерния изчислител.

С представената СДДФ искаме да дадем на читателя и друга гледна точка към проблемите на точните изчисления, за да може той да вземе най-правилния избор.

По-долу ще представим машинното изчисление на разглеждания пример в двоичната аритметика на стандарта IEEE 754. Най-напред ще представим операция изваждане.

Операция изваждане

Както и в ръчното изчисление, започваме с изваждане на нормализираните десетични мантиси

MS = MA-MB = 9675423 – 9675421 = 2 .

Действителното изображение на десетичните мантиси представлява техният двоичен еквивалент

MA(2) = 100100111010001010011111 ;

MB₍₂₎ = 100100111010001010011101 ,

който както се вижда заема напълно 24-битовото поле на двоичната мантиса според фигура 3.4.5.1.

Добре е известно, че операция изваждане се извършва с помощта на допълнителен код, така че числата първоначално представяме в прав код:

Изваждането изглежда както е показано тук

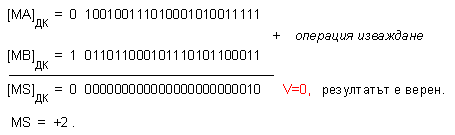
Следва да нормализираме получената мантиса и да определим новата стойност на порядъка на разликата според СДДФ. За целта трябва да получим 2/10-чния вид на мантисата. Последната е 7 разрядна. Тъй като двоичната стойност е само от два бита, то алгоритъмът за преобразуване има елементарно изпълнение и ние няма да го привеждаме. Получава се следния резултат

MA(10) = 0000 0000 0000 0000 0000 0000 0010 ;

Ще припомним, че споменатият алгоритъм е изложен раздел 3.6 на тази книга

http://www.tyanev.com/home.php?lang=bg&mid=18&mod=1&b=12&s=326 ,

а числени примери, които го илюстрират, могат да бъдат разгледани в книга [2], раздел 8.4.1.

http://www.tyanev.com/home.php?lang=bg&mid=18&mod=1&b=7&s=97

Нормализацията на десетичната мантисата представлява изместване наляво на 6 разряда

MA(10) = 0010 0000 0000 0000 0000 0000 0000 = 2000000 ;

В резултат на изместването се коригира и порядъкът, който става (-7). Така окончателно десетичната разлика има вида

В СДДФ това число ще се запише така

S = [ 0, 2000000, 1, 7 ] = [ 0, 000111101000010010000000, 1, 000111 ] .

Операция умножение

Следва да изчислим произведението P=S.C.

.

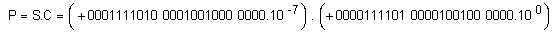Мантисите са цели двоични положителни числа и се умножават в прав код.

Десетично нормализиране на получената мантиса

Ще запишем нормализираното произведение така:

След събиране на порядъците на съмножителите, окончателният вид на произведението е:

Операция изваждане

Последното действие е изваждане R=P-D , което по-горе беше записано така:

Както и в ръчното изчисление, започваме с операция изваждане на нормализираните десетични мантиси, като преди това сме отчели, че порядъците на двата операнда P и D са еднакви.

MR = MP-MD = 2000000 – 1999920 = 80 .

Действителното изображение на десетичните мантиси представлява техният двоичен еквивалент

MP(2) = 000111101000010010000000 ;

MD₍₂₎ = 000111101000010000110000 ,

който както се вижда заема 24-битовото поле на двоичната мантиса според фигура 3.4.5.1.

Добре е известно, че операция изваждане се извършва с помощта на допълнителен код, така че числата първоначално представяме в прав код:

Изваждането изглежда както е показано тук

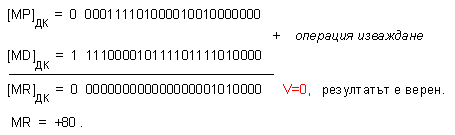
Окончателният резултат от изчислението на примерния израз се записва така:

И така, с представения числен пример и неговото изпълнение според изискванията на СДДФ считаме, че представената форма обезпечава изискваната точност каквато тя е в десетична бройна система. Ще завършим с това, че СДДФ изисква от конструкторите реализация на съответния хардуерен изчислител.

Сравнителни характеристики на СДДФ на числата

Ще изброим характеристиките на традиционната форма и представената тук, за да може да бъдат по-лесно тяхното сравнение. Допълнителни сведения читателят може да намери тук:

https://en.wikipedia.org/wiki/Half-precision_floating-point_format

1.

Мантисата на число, представено според стандарта IEEE 754, е двоично число от вида ± 1,bbb…bbb

Мантисата на число, представено в СДДФ, е цяло десетично число от вида ± dxxx…xxx, където d е десетична цифра, различна от нула. Тази десетична мантиса се представя от своя двоичен еквивалент ± bbb…bbb,

2. В поле с дължина 10 бита двоичната последователност от 10 единици (1111111111) е еквивалентна на десетичното число 1023. Следователно по-големи числа ще имат двоична дължина по-голяма от 10 бита и ще бъдат непредставими. Така всички десетични числа ≤ 999 ще могат да се представят точно в това 10 битово поле.

3. В IEEE 754 максималната нормализирана двоична мантиса има десетичния еквивалент

M_max = 1,1111111111 = 1,9990234375 .

Гарантираният брой верни десетични цифри, които могат да се получат след преобразуване на 11-битовата двоична мантиса е 3. Максималната 3-цифрена нормализирана десетична мантиса е

M_max = 999, .

Двоичният еквивалент на това число е 10-битово:

M_max = 1111100111, .

Това означава, че в СДДФ 3-цифрената мантиса може да се представя точно.

4.

Минималната нормализирана мантиса според IEEE 754 е Mmin = 1,0 .

Минималната нормализирана мантиса в СДДФ е Mmin = 100, . Двоичният еквивалент е Mmin = 0001100100,

5.

Максималното десетично число според IEEE754 е числото Mmax = 1,9990234375.2^31 = 4292870144 .

Максималното десетично число според СДДФ е числото Mmax = 999.10^31 .

6.

Минималната стъпка (дискретът) според IEEE 754 е числото h = 0,0000000001.2^-^1^5 = 3,0517578125.10^-5

Минималната стъпка (дискретът) в СДДФ е числото h = 100.10^-^1^5 = 1.10^-^13

Следващият раздел е:

§ 3.5 Логически операции, сравнения, измествания

(Logical operations, comparisons, shifts)

http://www.tyanev.com/home.php?lang=bg&mid=18&mod=1&b=12&s=325