§ 3.5 Логически
операции,
сравнения, измествания
Logical
operations, comparisons, shifts
Тъй
като един от
видовете
данни, чието
представяне
коментирахме
в глава 1, е
логическият,
тук ще
разгледаме
техническата
реализация
на
необходимите
за тяхната преработка
логически
операции.
Освен тях във
всеки
процесор е
реализирана
група операции,
които ние ще
причислим
към
логическите,
по причина на
това, че
получаваните
от тях
резултати
имат
логическа
интерпретация.
Най-често
реализираните
логически
операции са:
·
Операция
"Логическо
събиране",
(дизюнкция,
ИЛИ, OR);
·
Операция
"Логическо
умножение",
(конюнкция,
И, AND);
·
Операция
"Логическа
инверсия", (НЕ, NOT);
·
Операция
"Логическа
неравнозначност", (Сума
по mod2,
Изключващо
ИЛИ, XOR).
Съвкупността
от логически
операции
трябва да
бъде функционално
пълна,
свойство
което
обезпечава
изчисляването
на
произволни
логически
изрази.
Изброените
логически
операции се
реализират
само върху
основния
формат на
разрядната
мрежа. Когато
става дума за
променливи в
програма,
написана на
език от
високо ниво,
обикновено
те се
декларират
от логически тип,
чийто формат
е 1 байт (8 бита),
което определя
пределите за
изпълнение
на заявената
логическа
операция.
Тъй като логическите операции са определени само върху логическите константи, в многоразрядните процесори изпълнението им е поразрядно, например логическо умножение
![]()
генерира съответната логическа стойност за всеки бит поотделно по дължината на заявения формат. В този смисъл, съдържанието на участващите в операцията регистри се интерпретира като двоична комбинация, не притежаваща количествено значение.
Всяка
логическа
операция
формира
признаци на
резултата -
най-често
признак за
нула (Z),
признак за
четност (P),
съдържание
на знаковия
разряд (S).
Флагът за
пренос С (вижте
фигура 3.2.1.1),
който в
логическата
структура на
едно завършено
АЛУ е свързан
с връзките за
изместване
на
съдържанието
на
разрядната
мрежа, при
логически
операции
обикновено
се установява
в нула (С=0).
За
непосредствено
изпълнение
на тези
операции се
използуват
известни
логически
схеми. В
много
логически структури
тези
операции са
вградени в
многофункционалния
суматор на АЛУ,
чието
настройване
(инициализация)
към изпълнението
на дадена
функция се
постига чрез
подаване на
управляващия
му код (вижте книга [2], фигура 1.10).
С цел да се
намалят
апаратните
разходи, може
да се приложи
паралелно-последователен
метод за
изпълнение
на
логическите
операции,
което се
постига чрез
една
многофункционална
схема,
обработваща
само част от
разрядната
мрежа -
например 1[B]. По
този начин
съдържанието
на разрядната
мрежа с
дължина 4[B], ще
се обработи последователно,
байт след
байт, за 4
такта.
Към
логическите
операции се
отнася една специфична
операция
наречена "Логическо
сравнение"
или още "Логическо
тестване".
Тази
операция по
същество
представлява
операция
логическо
умножение, но
без фиксиране
на резултата.
След
изпълнение
на операцията,
източниците,
подавали
операндите, запазват
своето
съдържание. В
резултат на операцията
обаче се
формират и
запомнят
признаците
на
нефиксирания
резултат,
които
по-нататък
могат да се
използват
като условия
за
разклонения
в програмите.
Операции
"Сравнение".
Групата
операции от
тип
сравнение в
множеството
изпълними
операции е
относително голяма.
Сравнението
е действие, с
помощта на
което
алгоритмите
"се ориентират"
в хода на
обработката
на данните.
На сравнение
се подлагат
както числови,
така и
нечислови
данни.
Операцията "Сравнение"
има
аналогични
на
операцията "Логическо
сравнение"
цели - да
формира
признаците на
резултата,
без да го
фиксира и без
да променя
операндите.
Сравнението
в случая е акт
на проверка на
отношение
на първия
операнд
спрямо
втория
операнд:
X <=> Y (3.5.1)
Тъй
като
проверката
на едно
отношение
всъщност
дава отговор
на въпроса "Вярно
ли е
отношението?"
и тъй като
резултатът е
някое от
утвържденията:
"Да,
вярно е!", "Не,
не е вярно!",
имащи чисто
логически
смисъл, то
тези операции
могат да
бъдат
отнесени към
логическите.
Когато
операндите X
и Y са числа, то
непосредствена
проверка на
отношението
(3.5.1) не може да
се изпълни
поради
многообразието
на данните,
ето защо това
става чрез
преобразуване
на това
отношение в
еквивалентното
му, имащо
вида:
(X-Y) <=> 0
, (3.5.2)
или с
други думи,
по
отношението
на разликата
между операндите
към нулата
(т.е. по
признаците
на разликата)
се
установява
отговорът на
интересуващото
ни отношение.
И така,
при операция
сравнение се
извършва изваждане
на втория
операнд от
първия, без
да се фиксира
разликата.
Фиксират се
само нейните
признаци C,Z,S,P
и др., в
регистъра на
признаците
на резултата
(вижте фигура
3.2.1.1). В
цифровите
процесори това
прави
машинната
команда СМР
(Compare), но тук
трябва да
обърнем
внимание на
използвания
от нея
допълнителен
код и
аритметическо
събиране,
което я прави
една от
най-бавните
операции,
сравнима с
операции
събиране и
изваждане. Да
не забравяме,
че сравнения
се налага да
се
изпълняват и
между 2/10-чни
числа, а така
също и между
такива, представени
във форма с
плаваща запетая.
Операция
сравнение се
изпълнява непосредствено
преди
условни
преходи, които
използват
актуалните
стойности на
признаците
на резултата,
за да
реализират
алгоритмичните
преходи.
Ускоряване на операция сравнение може да се постигне чрез логическа схема на цифров компаратор, наличието на която в АЛУ все още се приема за излишен разкош. Тук, по-късно в следващ раздел ще бъде представен синтезът на цифров компаратор, който може да ускори разглежданата операция.
Към
групата на
логическите
операции още
могат да се
отнесат и
операциите
от тип "Изместване".
Операциите
от тип
изместване
са три вида:
·
"Логическо
изместване" ;
·
"Аритметическо
изместване" ;
·
"Циклическо
изместване" (Ротация) .
Според
посоката,
изместванията
са наляво
или надясно.
Операциите
от тип
изместване
са едноместни,
а това
означава, че
операндът е
един. Така съдържанието
на
разрядната
мрежа се
измества по
съответния
начин на един
разряд.
Когато
изместването
е на повече
разряди техният
брой или е
фиксиран
(чрез кода на
операцията),
или в структурата
на командата
се появява
втори операнд,
показващ
дължината на
изместването.
Логическото
изместване
се предлага
за изпълнение
и в двете
посоки.
Наричат се
логически,
защото
съдържанието
на
разрядната мрежа
се
интерпретира
като
логическа
комбинация. В
освободения
разряд на
разрядната
мрежа се
записва нула,
която е
символ на
опразването
на съответния
бит.
Излизащата
от
противоположния
бит на
разрядната
мрежа
двоична
цифра (или
още логическа
стойност), се
записва в
тригера за
пренос С от
регистъра на признаците
на резултата.
Изпълнението
се пояснява
чрез фигура 3.5.1.
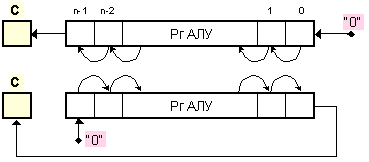
Фиг. 3.5.1.
Схеми за
логическо
изместване
Аритметическото
изместване
най-често се реализира
само в
посоката
надясно.
Нарича се
аритметическо,
тъй като съдържанието
на
разрядната
мрежа се
интерпретира
като число
със знак.
Изместването
трябва да е
свързано
само с
изменение на
теглото на
позициите на
числото, без
то да променя
знака си, ето
защо това
изместване
се изпълнява със
запазване
на
стойността в
знаковия бит
на
разрядната
мрежа, т.е. той
предава
своята
стойност в съседната
отдясно, но
не приема
нова
стойност,
като запазва
текущата си.
Може да
твърдим, че в
освободения
старши разряд
от цифровата
част на
разрядната
мрежа (бит №(n-2) – вижте
фигура 1.1.6.1.3) ), се
записва кода
на незначеща
старша цифра,
който според
теорията на
допълнителния
код съвпада
със
стойността
на знаковата
цифра (извод
№3 от таблица
1.6.2.1.2).
Аритметическото
изместване
надясно може
да се
интерпретира
като
операция
деление на
модула на
числото с
основата на
бройната
система q, (q=2).
Излизащият
от
разрядната
мрежа бит се
записва в тригера
за пренос С.
Възможни са
реализации
на
аритметическо
изместване
наляво, което
може да се
интерпретира
като
умножение на
модула на
числото с
основата на
бройната
система q, (q=2).
Аритметическото
изместване наляво
обаче е
твърде
опасна
операция, тъй
като при
нейното
изпълнение
може да се
получи
резултат,
който да е
непредставим
в смисъла на
аритметическата
му
интерпретация,
т.е. възможно
е да настъпи
аритметическо
препълване.
За такова
препълване
при изместване
не се
реализират
разпознаващи
схеми и отговорността
за
правилната
аритметическа
интерпретация
на резултата
от изместването
се носи от
програмиста.
Ето защо в
много реални
процесори
тази
операция не е
реализирана.
Ако трябва да
бъдем
по-прецизни,
следва да
кажем, че е в
сила
следното
правило – ако
при
изместване
наляво на
число
представено
в
допълнителен
код
знаковият
бит промени
стойността
си, то е
настъпило
препълване. При
това
изместване в
освободения
младши разряд
се въвежда
незначеща
цифра, т.е.
нула. В този
смисъл това
изместване е
аналогично
по
реализация с
логическото.
Изложените
обяснения са
илюстрирани
на фигура 3.5.2.
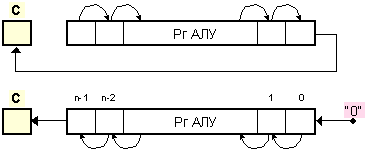
Фиг. 3.5.2.
Схеми на
аритметическо
изместване
Следващите
измествания,
на които ще
се спрем са
циклическите.
Те се
осъществяват
и в двете посоки
- и наляво и
надясно, като
могат да
бъдат реализирани
по два
начина: само
в разрядната
мрежа, или с
включване на
тригера за
пренос С. В
първия
случай,
когато
изместването
се извършва в
разрядната
мрежа, дължината
на
циклическата
верига е n[b], а във
втория
случай тя е (n+1)[b]. И в
двата случая
излизащият
(независимо от
кой край на
разрядната
мрежа) бит, се
запомня в
тригера за
пренос С.
Логическите
връзки,
поясняващи
ротациите, са
илюстрирани
на фигура 3.5.3.
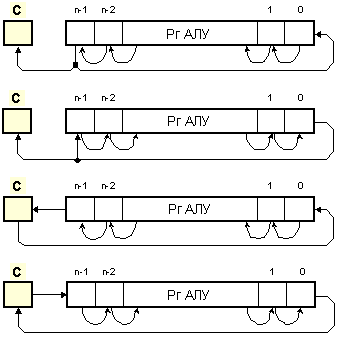
Фиг. 3.5.3.
Схеми на
циклическо
изместване
Операциите от тип изместване формират признаците на резултата по следния начин:
·
Тригерът
на знака S
приема
стойността в
най-левия
разряд на разрядната
мрежа;
·
Тригерът
на признака за
нула Z
приема
стойността
на флага за
нулево съдържание
на
разрядната
мрежа;
·
Тригерът
за паритет Р
приема
стойността
на флага за
четност/нечетност
на
съдържанието
на
разрядната
мрежа;
·
Тригерът
за
препълване V
приема
стойността
на
логическата
функция
![]()
Състоянието на останалите признаци най-често е без значение, а състоянието на тригера за пренос C беше пояснено на фигурите 3.5.1, 3.5.2 и 3.5.3.
Двуместните
операции от
тип
изместване могат
да бъдат
изпълнени с
помощта на
едноразрядни
изместващи
структури
чрез
организиране
на цикъл на
микропрограмно
ниво. За
целта операндът,
показващ
дължината на
изместването
(броя на
разрядите),
се зарежда в
изваждащ
брояч, с
чиято помощ
се
организира
цикъла на
изместването.
Ако обаче е
необходима висока
скорост на
операция
изместване,
трябва да се
използуват
програмируеми
изместващи
матрици,
които ще
бъдат
разгледани
по-долу.
Ефективното
изместване
при това ще
има
мултиплициран
ефект, като
се има
предвид, че
изместванията
са
съществена
част от алгоритмите
за умножение,
деление,
нормализиране
и т.н.
Известни
са два вида
програмируеми
схеми за
изместване - матрични
и йерархични
(каскадни). В
основата на
логическия
синтез на
тези схемите
стои
споменатата
вече
интерпретация
на операция
изместване -
умножение с
числото 2k или
деление с
числото 2(-k),
където k е
дължината на
изместването.
За разлика от
схемните
умножители, в
случая,
когато множителят
има вида 2(±k),
какъвто е
случаят тук,
всички
поразрядни произведения
са нули, с
изключение
на едно. Това
позволява
последователното
събиране на
поразрядните
произведения
да бъде
заменено с
тяхното
едновременно
логическо
събиране.
Примерни
логически
структури на
изместващи
матрици за 4-разряден
операнд с
изместване
на 0, 1, 2, 3 разряда,
са показани
на фигура 3.5.4.
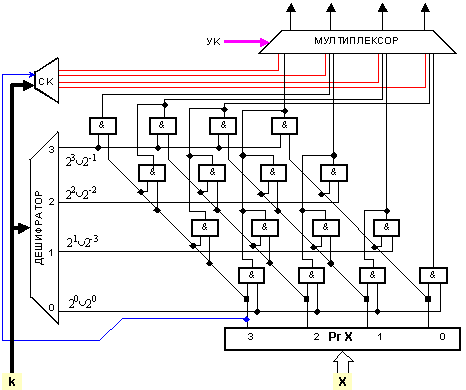
Фиг.
3.5.4. 4-разрядна
изместваща
секция с
диагонална матрица
наклонена
наляво
Както
се вижда от
фигура 3.5.4,
изместващите
структури
съдържат
следните
възли:
изместваща
матрица от
двувходови
схеми И,
дешифратор
на параметъра
на
изместване k,
изходен
мултиплексор,
схема за
корекция при
аритметични
измествания СК.
Съдържащата
се в регистър
РгХ
комбинация Х
излиза на
изходите на
мултиплексора
съответно
променена.
Факторите за
тази промяна
са два –
параметърът k и
управляващият
код УК.
Логически
схеми И
в
изместващата
матрица са
подредени
диагонално в
посока
наляво.
Изходите на
тези схеми са
свързани
накъсо и
образуват
така нареченото
"Опроводено
ИЛИ", което
реализира
споменатото
по-горе логическо
събиране.
Изходите на
опроводените
ИЛИ са
подключени
към изходния мултиплексор
така, че в
зависимост
от управляващия
код УК,
който му се
подава, се
изпълнява
една от операциите
ляво, дясно
или
ротационно
изместване. В
този смисъл
изходният
мултиплексор
е значително
по-сложна
схема, тъй
като в този
случай е
функционално
по-богата.
Броят на
разрядите, на
които се
извършва
изместването,
се дешифрира,
при което изходите
на
дешифратора
управляват
схемите И в
изместващата
матрица.
Параметърът
на изместването
k
следва да се
възприема
като число
със знак (±k) и
като такова
то
трябва да
бъде
представено
в
допълнителен
код.
Програмируемото
изместване е
възможно във
вариант с
дясно
наклонена
изместваща матрица.
Този вариант
е представен
на фигура 3.5.5. В
логическата
структура от
фигура 3.5.5,
поради
обратния
наклон на
връзките в
изместващата
матрица,
параметърът
се представя
в
допълнителен
код, но с
инвертиран
знак, т.е. (-(±k)). Ако
параметърът
на
изместването
k
е представен
по модул,
това налага
специално
изпълнение
на
дешифратора,
за да бъде
отчетена
посоката на
изместване.
Схемата
за корекция СК при
аритметически
измествания
представлява
дешифратор,
който
изработва
група от k на
брой
незначещи
цифри, които
при изместването
надясно,
зависят от
знака на
изходното
число, т.е.
изпълнява се
така
нареченото
знаково
разширение
на числото.
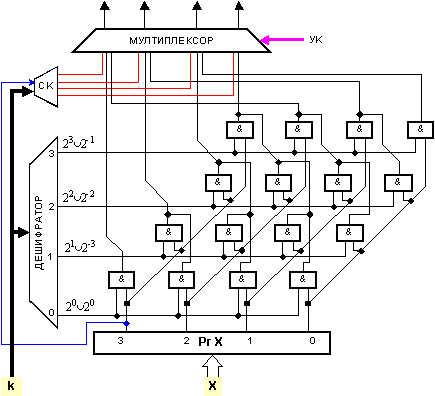
Фиг.
3.5.5. 4-разрядна
изместваща
секция с
диагонална матрица
наклонена
надясно
Освен
чрез
диагонални
изместващи
матрици,
многоразрядните
еднотактни
изместващи
схеми могат
да се
построят
чрез
правоъгълни
изместващи
матрици,
както е
показано на
фигура 3.5.6.
Всички схеми И в
даден ред на
тази схема
имат общо
управление,
свързано към
съответния
изход на дешифратора
на
параметъра
на
изместването,
а всички
изходи на
схемите И в дадена
колонка, са
свързани с “опроводено
ИЛИ”.
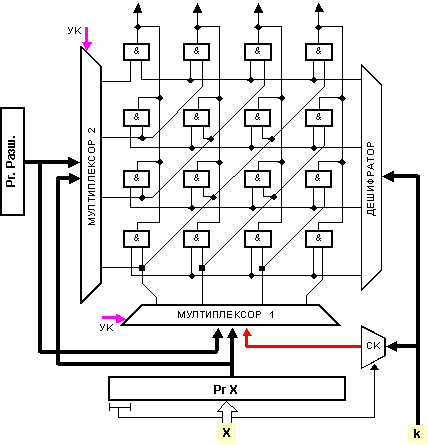
Фиг. 3.5.6.
Изместваща
секция с
правоъгълна
матрица
Информационните
входове на
схемите И са
свързани
диагонално,
при това
половината
от тях са
подключени
към входния
мултиплексор
MUX1, а
другата
половина към
входния
мултиплексор
MUX2. Тези
мултиплексори
са
двувходови и
са свързани с
регистъра на
входното
число РгХ
и регистъра
на
разширението
РгРазш.
Регистърът
на
разширението
РгРазш
е
предназначен
да съхранява
разрядите, постъпващи
при
изместването
в
освобождаващите
се разряди.
Когато
е назначено
изместване
наляво, цифрите
на числото Х
постъпват
през
мултиплексора
МUX1 в
изместващата
матрица. В
същото време
през MUX2
постъпват
цифрите на
разширението.
При изместване
надясно,
цифрите на
числото Х се
подават през MUX2, а
тези на
разширението
- през MUX1.
При
аритметическо
изместване
надясно, през
първия
мултиплексор
постъпват
цифрите на
размножения
знак.
Правоъгълната
матрица може
да бъде построена
и с обратно
наклонени
диагонални
връзки, при
което
мултиплексорите
сменят местата
си.
Построяването
на
дешифратора
на параметъра
на
изместването
е аналогично
на разгледания
в
предходната
логическа
структура.
При
изпълнение
на
циклическо
изместване и
през двата
мултиплексора
постъпват
цифри само от
регистъра на
изходното
число.
Разгледаните
схеми
осигуряват
изместване в
рамките на
разрядната
мрежа. Ако
обаче дължината
на
разрядната
мрежа е
по-голяма от
дължината на
максималното
изместване, което
може да
реализира
изместващата
секция, то
или трябва да
се проектира
нова
изместваща
матрица, или
към
съществуващата
да се добавят
възможности
за:
микропрограмно
паралелно-последователно
изместване,
или за каскадно
разширяване.
Паралелно последователното изместване се реализира на два етапа - изместване на порциите и изместване вътре в порциите. Така например изместване на 14 разряда с 4-разрядни секции може да се осъществи така: зареждане на порциите във входните регистри през 3 секции, което осигурява 3.4=12 разряда и изместване на още два разряда в рамките на всяка секция, с което се достига общата дължина.
Под
каскадно или
апаратно
разширение
на възможностите
за
изместване
се разбира някакво
обединяване
на секциите
за изместване
в обща
структура за
паралелна
обработка на
всички
разряди на
разрядната
мрежа.
Синтезът
и
изследването
на схеми за
изместване,
съответствуващи
на случая,
когато (n>k), оставяме
на читателя.
В много литературни източници читателят може да намери технически решения за програмируеми изместващи матрици, използващи най-често елементарни 2-входови мултиплексори. Тук по-долу ще осветлим и този подход, така че читателят да има по-богат поглед, свързан с темата за да може да се справя по-лесно с изучаването на различни решения, които ще среща в литературата, както и за да може да проектира възможно най-оптимално своите решения.
Най-напред
ще
представим
програмируема
логическа
схема за
изместване
наляво на 4-битова
комбинация.
Изместванията,
които имат
смисъл при
тази дължина
са на 0, на 1, на 2
или на 3 бита.
Както се
вижда, възможностите
са 4, което
означава, че
изместването
ще се
инициализира
от 2-битова
управляваща
комбинация,
при следната
кодова
таблица
Таблица
3.5.1
Изместващ
код
|
Кодова
комбинация S1, S0 |
Изместване
на входната комбинация
X |
|
0 0 |
Y = X (изместване
на 0 бита) |
|
0 1 |
Y = X.2
(изместване
на 1 бит) |
|
1 0 |
Y = X.4
(изместване
на 2 бита) |
|
1 1 |
Y = X.8
(изместване
на 3 бита) |
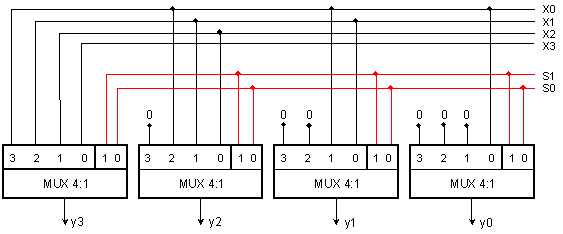
Фиг. 3.5.7. Програмируема
схема за
изместване
наляво на 4
битова
комбинация
След подходящо опроводяване от горната схема може да се получи схема за циклическо изместване наляво, която е представене на следващата фигура.
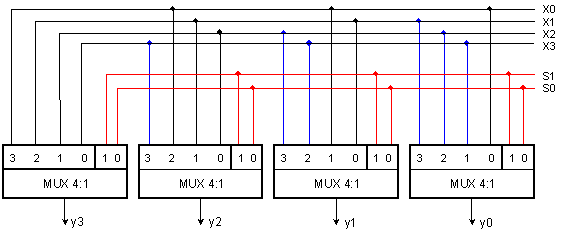
Фиг. 3.5.8. Програмируема
схема за
циклическо
изместване
наляво на 4
битова
комбинация
Таблица
3.5.2
Циклическо
изместване
|
Кодова
комбинация S1, S0 |
На
изхода Y (y3,y2,y1,y0) излиза
завъртяна
комбинация |
|
0 0 |
x3, x2, x1,
x0 (изместване
на 0 бита) |
|
0 1 |
x2, x1, x0,
x3 (изместване
на 1 бит) |
|
1 0 |
x1, x0, x3,
x2 (изместване
на 2 бита) |
|
1 1 |
x0, x3, x2,
x1 (изместване
на 3 бита) |
Прилагайки
представения
кратко
подход, чрез
различни
мултиплексори,
читателят може
да проектира
необходимата
му схема.
В
някои
съвременни
логически
структури с микропрограмно
управление,
операциите от
тип
изместване
са
комбинирани
с операциите
събиране и
изваждане,
при което се
получават нови
изпълними
операции.
Тези
операции се
именуват:
·
"Събиране
с изместване
надясно" , "Събиране
с изместване
наляво" ;
·
"Изваждане
с изместване
надясно" , "Изваждане
с изместване
наляво" .
Наличието
на такива
комбинирани
операции
позволява да
се
реализират
на микропрограмно
ниво бързи
алгоритми за
операциите умножение,
изчисляване
на функции,
както и други
специализирани
изчисления.
При тези
операции
първо се извършва
аритметическата
операция, но
признаците
на резултата
се формират след
съответното
изместване.
Така
например, при
събиране
(изваждане) с
изместване
надясно, в
най-старшия
разряд на разрядната
мрежа, след
изместването
се записва
преносът от
знаковия разряд,
който се е
получил при
аритметическата
операция. При
това в
тригера на
преноса С се
запомня
най-младшата
цифра на
междинния
резултат.
Останалите
признаци се
определят
така -
тригерът за
препълване V
се нулира, а
тригерът на
знака S и
тригерът на
признака
нула Z се
определят
както при
операциите
от тип изместване
надясно.
Операция
събиране
(изваждане) с
изместване
наляво се
изпълнява
аналогично -
първо
аритметичната
част, след
това изместване
наляво. При
това
най-младшият
разряд на
резултата
приема стойност
"0", а
признаците
му се
определят
както следва:
·
Тригерът
V
приема
стойността
на флага за
препълване, което
е възможно
както на
етапа на
аритметическата
операция,
така и на
етапа на
логическата
операция;
·
Тригерът
на преноса С
приема
най-старшата
цифра на
междинния
резултат -
сумата
(разликата);
·
Тригерите
на знака S и
признака за
нула Z
приемат
флаговете
както при
операция изместване
надясно.
Към
логическите
операции
могат да
бъдат причислени
и операциите
по обработка
на части от
разрядната
мрежа. Най-малката
част от
разрядната
мрежа това е 1[b].
Върху този
бит (разряд)
могат да се
определят
следните
операции:
·
Нулиране
;
·
Установяване
;
·
Инвертиране
;
·
Запис
в тригера на
признака за
препълване V от
регистъра на
признаците
на резултата.
За
изпълнение
на тези
операции е
необходимо
да се посочи
номерът на
разряда в
разрядната
мрежа. Този
номер
представлява
операнд, а
тези
операции се
определят
като
едноместни.
Операциите
върху част от
разрядната
мрежа с
дължина
по-голяма от 1[b]
могат да
бъдат следните:
·
Нулиране
;
·
Установяване
;
·
Инвертиране
;
·
Изместване
.
Частта
от
разрядната
мрежа, която
се подлага на
операцията,
се определя
от две граници
- едната
винаги
започва от
разряда с
указания
номер
(включително),
а другата
граница представлява
най-левия или
най-десния
разряд на
разрядната
мрежа, според
указаното
направление
(наляво или
надясно). Номерът
на избрания
разряд се
кодира
съвместно с
посоката.
Значителна
част от
времето на
един процесор
с общо
предназначение
се
изразходва
за операции
от тип "Прекодиране
и
Редактиране
на символни
низове".
Тази работа е
свързана
преди всичко
с обработката
на потока от
информация,
постъпващ от
потребителя
или излизащ
към потребителя,
който
използува
най-разнообразни
периферни
устройства.
Така
например,
когато в процесора
информацията
е кодирана с
помощта на
таблицата MIK, а
информацията
(символът)
трябва да се
подаде на
терминал,
чийто
стандарт е
например KOИ-8, се
налага
операция
прекодиране.
Прекодирането
се извършва с
помощта на
прекодиращи
таблици,
запомнени в
паметта на компютъра.
Символите са
разположени
в паметта
така, че
техният код
(техният
пореден номер)
се използува
като
отместване
спрямо началния
адрес на
прекодиращата
таблица. Например
ако символът
от кода MIK е "Я", той се
представя от
поредния си
номер в тази
таблица (вижте
глава 1, пункт
1.1.5 – ASCII-таблицата), т.е. от
числото 159. За да се
прекодира в
кода КОИ-8, по
отместване 159
в
прекодиращата
таблица
трябва да
бъде записано
числото 241, което
представлява
кода на същия
символ в новата
кодова
таблица. За
обратното
преобразувание
в
прекодиращата
таблица по
отместване 241
следва да се
намира
съдържанието
159.
Операция
прекодиране
може да има
разновидности
- например "Прекодиране
с проверка".
Същността на
тази
разновидност
е паралелно с
прекодирането
да се извършва
и проверка с
цел
откриване на
пунктуалните
знаци, чрез
които
най-често се
кодират
различните
разделители
(ограничители)
в символните
низове
(файлове).
Тези
операции
имат за
операнди
символни низове
с ограничена
дължина или с
променлива
дължина.
Съществуват
още операции
от тип "Редактиране", чиято
същност е
значително
по-сложна.
Например
символната
последователност,
изобразяваща
едно
десетично
число,
въвеждано от
клавиатурата,
трябва да се
отредактира
за
представяне
в обявения
формат и
обявената
форма на
двоично
число. В
рамките на
тези действия
се извършва
преобразуване
на постъпващото
число от
непакетиран
в пакетиран
десетичен
формат,
преобразуване
от десетична
бройна
система в
двоична,
представяне
във форма с
фиксирана
или с плаваща
запетая при
това в
обявения
формат.
В
по-прости
случаи,
редактирането
се интерпретира
като
налагане на
шаблон
(определение
на езикова
структура),
според която
лесно се
осигурява
вмъкване или
изхвърляне на
символи -
например
според
дефиницията
за структурата
<име
на файл>.
Този тип операции обикновено не изменят текущото съдържание на признаците на резултата.
Следващият
раздел е:
( Logic
Scheme for Determining the Number of Leftmost Insignificant Digits in a Bit-Set
of Any Length )