3.5.1
Логическа
схема за
определяне
броя на
старшите
незначещи
цифри в
разрядна мрежа
с произволна
дължина
Logic
Scheme for Determining the Number of Leftmost Insignificant Digits in a Bit-Set
of Any Length
В
предходният
раздел бяха
представени
различни програмируеми
изместващи
матрици.
Тяхното
програмиране
се състои в
подаване на
число k,
което
инициализира
логическата
схема за съответния
брой битове
на
еднотактното
изместване.
Именно
необходимостта
от този параметър
определя
изместващите
матрици като
програмируеми.
Тук ще бъде
разгледан
проблемът с
автоматичното
определяне
на стойноста
на този
параметър.
Решението на
този проблем
е
публикувано
от автора и
може да се
открие по
следния
адрес:
но
за пълнота на
разглежданата
тук тематика,
беше
преценено, че
е полезно то
да бъде представено
отделно в
настоящия
раздел.
Една
от
възможностите
за
повишаване
на производителността
на цифровите
устройства
на
микрооперационно
ниво се
съдържа в ускоряване
на
микрооперация
изместване. В
алгоритмите
за
изпълнение
на различни
аритметически
и логически
операции се
налага да се
извършва
изместване
на
съдържанието
на разрядната
мрежа. В
алгоритъма
на операция
деление
например се
налага да се
извършва лява
нормализация
на делимото и
делителя. В
алгоритмите
за обработка
на числа с
плаваща
запетая също
се налага да
се изпълнява
изместване наляво,
с цел
нормализация.
Каквато и да
е причината
за лява
нормалност
на
съдържанието
на
разрядната
мрежа, става
дума за изхвърляне
на старшите незначещи цифри,
допълващи
числото
отляво.
Например, нека
разрядната
мрежа е
16-битова (n=16) и в
нея да е
представено
в прав код
цялото число
(-52). Тогава
двоичното
съдържание
на
разрядната мрежа
ще бъде
следното

Както
се вижда от
горната
рисунка,
между знаковия
бит №(n-1) и
най-старшата
цифра 1 в
модула на
числото,
разрядната
мрежа е
запълнена с 9
нули. Тези
цифри са
незначещи за
числото. Лявата
нормализация
на числото
(необходима
например в
алгоритъма
за деление)
може да бъде
постигната
след 9
едноразрядни
измествания
наляво. Така
числото добива
вида
1 110100000000000 .
Достигането
на този вид
на числото
чрез 9 последователни
едноразрядни
измествания наляво
е достатъчно
бавен процес,
което е причина
за търсене на
високо
скоростно еднотактно
изместване.
Броят k на
изместванията
в общия
случай, за
n-битова
разрядна
мрежа,
съдържаща
число със
знак, се
променя в
интервала
![]()
Така за
горния
пример имаме
k=9.
Високо
скоростно
(еднотактно)
изместване
наляво на
произволен
брой битове
се реализира
чрез
програмируеми
изместващи
матрици от
вида,
представени
в предходния
раздел.
Параметърът,
с който
такива схеми се
инициализират
(програмират),
е числото k,
определено
по-горе. Така
възниква
задачата за
автоматично
формиране на
стойността
на този
параметър.
Автоматичното
формиране на
числото,
показващо
дължината на
необходимото
изместване,
следва да се
постигне с апаратни
средства.
Логическият
синтез на
схема, която
ще формира
стойността
на числото k, следва
да преодолее
следните
начални
проблеми:
1.
Стойността
на числото k
варира в
определения
по-горе
интервал. В
общият
случай k следва
да се получи
като m-битово
двоично число,
оценено
както следва
![]()
Тъй
като
разрядността
m на
числото k е
функция от
дължината на
разрядната
мрежа n, то следва,
че
логическата
схема за
формиране на
числото k
може да бъде
синтезирана
само за
постоянна
дължина на
разрядната
мрежа. Всяко
изменение в
дължината на
разрядната
мрежа, или на
формàта за
представяне
на числото,
ще изисква
синтез на
нова логическа
схема.
Синтезът на
нова
логическа схема
за формиране
на числото k в
условията на
динамично
изменение на
формàта е
невъзможно.
Още повече
такъв синтез
е невъзможен
при вече
реализирана
изчислителна
структура.
2. Лявата
нормализация
е изискване,
което се налага
върху
различни по
вид и по
форма числа,
явяващи се в
разрядната
мрежа, като
например
цели без
знак, цели
със знак,
дробни със
знак. Освен
това те могат
да будат
представени
в прав или в
допълнителен
код. Известно
е, че в
инверсните
машинни
кодове
(обратен и
допълнителен)
старшите
незначещи
цифри
съвпадат със
знаковата
цифра. С други
думи като
незначещи
цифри могат
да бъдат
видяни както
цифра нула,
така и цифра
единица
Известно е
още, че
старшата
значеща
цифра в
модула на
отрицателните
числа, представени
в
допълнителен
код, може да
бъде както
нула така и
единица, т.е.
тя е
изменчива.
За обезпечаване на променливия формат при представяне на числата е необходима адаптивност в известна степен на логическата схема. В тази връзка се налага извода, че крайното решение за логическата схема трябва да се търси чрез мултиплициране на една градивна логическа схема, синтезирана за част от разрядната мрежа. Тази част следва да бъде с минимална дължина. При наличието на такъв градивен елемент с възможност за каскадно свързване, става възможно реализиране на произволна дължина за входния аргумент. На този етап от анализа на проблема може да бъде приета за минимална дължината от три (3) бита. Дължината на група от три незначещи цифри ще доведе до оползотворяването на всички възможни комбинации на 2-битовия резултат (k=0,1,2,3), който може да бъде формиран за нея. Това означава, че анализът на двойно по-дълга част от разрядната мрежа ще изисква конкатениране на два градивни елемента. При това общият резултат ще бъде сумата
![]()
Така
окончателната
стойност за числото
k
може в общия
случай да се
изрази така
![]()
където
с i е
означен
номерът на
текущия
3-битов
градивен
елемент, a с r е
означен
броят на
градивните
елементи,
покриващи
дължината от
(n-1) бита
![]()
Имайки
предвид, че
старшата
значеща
цифра в
модула на
числото може
да се намира
във всяка от
позициите
вдясно от
знаковата, то
следва, че първият
градивен
елемент трябва
да обработва
позициите с
номера (n-2), (n-3) и (n-4) (при
числа със
знак). При
такова
позициониране
знаковият
бит не е
включен в
анализа. От това
следва, че
всеки
следващ
градивен елемент
трябва да
допълва отдясно
вече
поставените.
С други думи,
има се
предвид, че
номерата на
градивните
елементи ще
се променят
отляво
надясно в
низходящ ред
(r-1), (r-2),
2, 1, 0, както е
показано на
фигура 3.5.1.1.
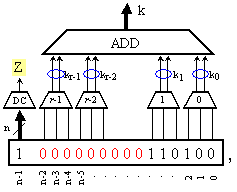
Фиг.
3.5.1.1.
Логическа
структура на
схемата
В
логическата
структура се вижда,
че е включен
и двоичен
суматор ADD,
който
реализира
сумата (3.5.1.4). Що
се отнася до
изменчивата
природа на
незначещите
цифри в допълнителния
код на
числата със
знак, този проблем
може да бъде
разрешен от
знаковия бит,
позовавайки
се на
изказаната вече
зависимост,
според която
незначещите
старши цифри
съвпадат със
знаковата.
Разбира се,
необходимо е
да се
определя
позицията на
старшата
значеща
цифра, при
това следва
да се изключи
наличието на
пълна нула в разрядната
мрежа, тъй
като тогава
всякакво изместване
на
съдържанието
й е
безсмислено.
Нулево
съдържание в
разрядната
мрежа може
лесно да бъде
дешифрирано
и формираният
при това
признак Z (zero) да
преопредели
числото k=0, ако
е необходимо.
В следствие
на описаното
по-горе
позициониране
на градивните
елементи в
посока
отляво
надясно, в
схемата
се изявява
проблем с
най-младшия
елемент. Този
елемент с №0,
както всеки
от
останалите, има
три входа.
Възможността
обаче те да
бъдат реално
подключени
не е
гарантирана,
тъй като
общата
дължина от
разрядната
мрежа, която
трябва да
покрие
схемата, може
да не бъде
кратна на 3.
При това са
възможни три ситуации
в групата с №0
остава един
бит, два бита
или три бита.
Последният
случай не е
проблемен.
Случаят,
когато е
останал
неподключен
само един
бит, е особен
с това, че ако
числото в
разрядната
мрежа е нула,
то числото k е
без смисъл, а
ако
съдържанието
на разрядната
мрежа е
различно от
нула, то
числото k е вече
формирано в
схемата от
предходните
градивни
елементи. Ако
обаче
съдържанието
на
разрядната
мрежа е единица,
то следва, че
единствената
значеща цифра
се намира в
най-младшия
разряд. В
този случай
за тази група
се получава
стойността k0=0.
С други думи,
в този случай
включването
на градивен
елемент
върху група
от един бит не
е необходимо,
защото
резултатът
от нейното
функциониране
е
предопределен.
Така общият
брой
градивни
елементи ще
бъде (r-1).
В случая когато са останали два младши бита, за групата са възможни два резултата:
1.
k0=0, ако в
тези два бита
има
комбинация 10
или 11;
2.
k0=1, ако в
тези два бита
има комбинация
01 или 00. В
последната
ситуация признакът
Z
следва да
игнорира
изчисляването
на числото k.
Така реален
остава само
резултатът k0=1,
съответстващ
на
комбинация 01.
В крайна сметка,
логиката на
описаните
възможности
се изразява
чрез
уравнението
![]()
Ако
казаното
по-горе може
да се отнесе
до положителните
числа, както
и до тези със
знак,
представени
в прав код, то
следва да
бъдат разгледани
отрицателните,
представени
в обратен или
в
допълнителен
код. Както е
пояснено в
точка 2 по-горе,
в тези случаи
старшите
незначещи
цифри на
числото в
разрядната
мрежа се
определят от
знаковата,
т.е. те са
единици. При
позициониране
на последния
градивен
елемент са
възможни
описаните
по-горе
ситуации. Ако
е останал
неподключен
само един бит
(b0) (виж
фиг.3.5.1.1), то той
може да
съдържа
незначеща или
значеща
цифра.
Анализът на
този случай води
до
аналогичен
резултат,
формулиран за
положителните
числа, т.е. k0=0.
В случая, когато са останали два младши бита, за групата са възможни следните резултати, които зависят от кода.
Ако
кодът е
обратен, то
1.
k0=0, ако в
тези два бита
има
комбинация 01
или 00;
2.
k0=1, ако в
тези два бита
има
комбинация 10
или 11. В последната
ситуация
признакът Z
следва да
игнорира
изчисляването
на числото k.
Така реален
остава само
резултатът k0=1,
съответстващ
на
комбинация 10.
Така логиката
на описаните
възможности
се изразява чрез
уравнението
![]()
Ако
кодът е
допълнителен,
то
1.
k0=0, ако в
тези два бита
има
комбинация 10
или 00;
2.
k0=1, ако в
тези два бита
има комбинация
01 или 11.
Тук
логиката за
числото k може да
се изрази
така
![]()
След
така
представения
анализ и
формулираните
изводи ще
изложим
логическия
синтез на
схемата.
Както вече
беше решено,
ще бъде
търсено
решение, при
което
логическата
схема на
градивния
елемент ще
има три входни
аргумента ( b2 b1 b0 )
битове на i-тата
група.
Групите от по
3 бита ще се
формират
както е
показано на
фиг.3.5.1.1, т.е. отляво
надясно,
започвайки
от бит №(n-2).
Покриването
на разрядна
мрежа с
произволна
дължина ще
става с
последователно
включване на
градивния
елемент,
както вече
беше предложено.
При тази
постановка
всеки елемент
има за задача
да открие
старшата
значеща
цифра на
съдържащото
се в
разрядната мрежа
число. Ако
даден
елемент
постигне това,
работата на
стоящите
вдясно от
него елементи
се
обезсмисля.
Техните
резултати
трябва да
бъдат нула.
Последното
означава, че
между
градивните
елементи има
функционални
връзки, които
следва да
бъдат
изяснени. Всеки
градивен
елемент има
смисъл да
анализира групата
от разряди,
към които е
подключен,
ако
предходния
елемент не е
открил
старша значеща
цифра в
числото. Така
става ясно,
че два
съседни
елемента
трябва да
бъдат свързани
със сигнал p (permission),
който
генерира
ляво
стоящият и се
използва от
дясно стоящия
в качеството
на
разрешение.
Казаното е
илюстрирано
на фигура 3.5.1.2.
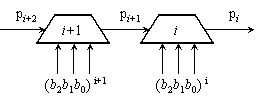
Фиг.
3.5.1.2.
Структура
за
генериране
на сигнал разрешение
Логиката на
сигнала p се
дефинира
като изходна
функция
както следва
![]()
която
следва да се
разбира така.
Градивният
елемент
генерира
разрешение
към следващия
елемент (pi=1) в
два случая,
при условие
че самият той
е получил
разрешение (pi+1=1):
·
Когато
числото в
разрядната
мрежа е положително
(s=0) и
входната
3-битова
комбинация е
от нули (b2b1b0 = 000);
·
Когато
числото в
разрядната
мрежа е отрицателно
(s=1), входната
3-битова
комбинация е
от единици (b2b1b0 = 111).
В
останалите
случаи,
когато
схемата на
градивния
елемент не
разпознава
във входната
3-битова
комбинация
група от незначещи
цифри, или
когато е
получила
сигнал за
забрана да
функционира (pi+1=0),
тя генерира
сигнал за
забрана към
следващия
елемент (pi=0)
(фиг. 3.5.1.2).
Както
се вижда в
определението
(9), за текущата
тройка
входни
битове са
включени две
от възможните
комбинации - (000)
и (111). Става дума
за старши
незначещи
цифри на
числа
представени
в допълнителен
код, когато
незначещите
цифри съвпадат
със
знаковата.
Сега
ще изложим
още някои
съображения
относно
отрицателните
числа в
допълнителен
код. Както
беше изтъкнато
по-горе
положителните
числа не
създават
особени
ситуации при
разпознаване
на групата,
съдържаща
старшата
единица в числото.
За разлика от
тях,
отрицателните
числа,
представени
в
допълнителен
код, създават
такива,
изразяващи
се в
променящата
се стойност
на старшата
значеща
цифра на
числото, която
за някои
числа е нула,
а за други
единица. За
преодоляване
на това
изключение и
в помощ на
логическия
синтез е
направен
следният
анализ.
По-долу
са
разгледани
примери с
отрицателни
числа в
допълнителен
код, имащи
старша
значеща
цифра нула и
отделно числа
със старша
значеща
цифра
единица. В
примерите
старшата
цифра се
намира в
различните
възможни
позиции на
текущата
тройка битове.
Примерите
показват, че
разпознаването
на старшата
значеща
цифра като
нула или като
единица, е
функция от
комбинацията
на дясно
стоящите
битове.
Първите три
примера илюстрират
отрицателно
число в
допълнителен
код със
старша
значеща
цифра нула,
намираща се в
различни
позиции на
текущата
тройка
битове:
(1 111111000000001000), k1=3;
(1 111110000000001000), k1=2;
(1 111100000000001000), k1=1;
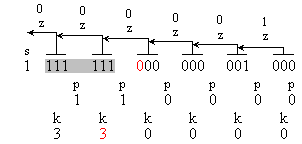
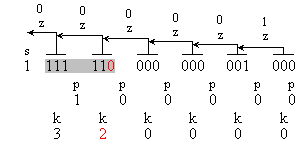
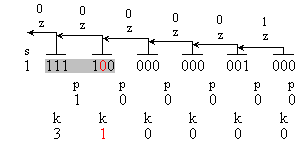
Следващите
три примера
илюстрират
отрицателно
число в
допълнителен
код със старша
значеща цифра
единица,
намираща се в
различни
позиции на
текущата
тройка
битове.
(1 111111000000000000) , k1=2;
(1 111110000000000000) , k1=1;
(1 111100000000000000)
, k1=0;
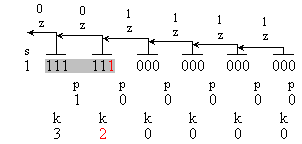
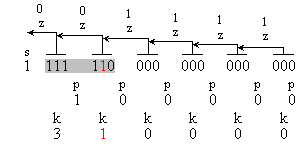
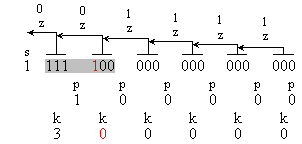
Както е
показано на
рисунките
по-горе, всяка
тройка
битове се
дешифрира с
цел да се открие
нулевата
комбинация (000),
което е
задача на
функциите zi (zero).
Дешифрирането
по групи е
последователно
отдясно
наляво. За
разпознаване
на двойствеността
на старшата
значеща
цифра в отрицателни
числа (0 или 1)
спомага
каскадното
умножение на
тези функции.
Възможни са
две
последователности
от функции zi,
както е
показано на
горните
примери:
·
Последователното
каскадно
логическо умножение
на
стойностите
на функциите zi
в посока
към старшите
разряди
достига със стойност
нула групата,
в която се
намира старшата
значеща
цифра нула (първата
група
примери);
·
И
последователното
каскадно
логическо умножение
на
стойностите
на функциите zi
в посока
към старшите
разряди
достига със
стойност
единица
групата, в
която се
намира
старшата
значеща цифра
единица (втората
група
примери).
Така
всяка
функция zi
се
контролира
от
предидущата zi-1
според
следната
логика
![]()
В
представените
примери за
всяка група
от 3 бита са
показани
стойностите
на функциите z, p и k, генерирани
от
примерното
съдържание
на разрядната
мрежа.
В
резултат на
този анализ
следва, че
всяка градивна
схема се
атакува
отдясно от
функция z, а
отляво от
функция p. Освен
това всяка
група се
инициализира
от функцията
на знака на числото
s. Така
логическите
аргументи на
3-битовата градивна
схема могат
да се
илюстрират
чрез структурата
от фиг. 3.5.1.3.
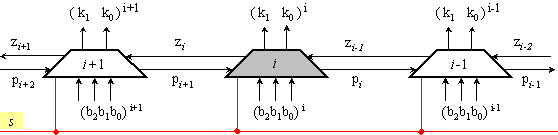
Фиг.
3.5.1.3.
Аргументи и
функции на
градивната схема
След
така
изяснената
обща
структура и
функционалност,
логическата
схема на
градивния елемент
може да бъде
синтезирана
от съставената
за целта
непълна
таблица на
истинност.
Изложеният
анализ
определя
всички аргументи
на градивния
елемент,
техният
смисъл, както
и
функционалните
връзки между
тях. Определени
са и
изходните му
функции.
Пълното описание
на логиката
за
функциониране
на градивния
елемент е
изразена в
таблица на
истинност.
Таблица
1. Таблица
на истинност
|
|
Вход
елемент №(i) |
Изход
елемент №(i) |
||||||||
|
№ |
pi+1 |
s |
b2 |
b1 |
b0 |
zi-1 |
k1 |
k0 |
zi |
pi |
|
1 |
0 |
* |
* |
* |
* |
* |
0 |
0 |
0 |
0 |
|
2 |
1 |
0 |
0 |
0 |
0 |
* |
1 |
1 |
0 |
1 |
|
3 |
1 |
0 |
0 |
0 |
1 |
* |
1 |
0 |
0 |
0 |
|
4 |
1 |
0 |
0 |
1 |
* |
* |
0 |
1 |
0 |
0 |
|
5 |
1 |
0 |
1 |
* |
* |
* |
0 |
0 |
0 |
0 |
|
6 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
7 |
1 |
1 |
0 |
* |
* |
0 |
0 |
0 |
0 |
0 |
|
8 |
1 |
1 |
1 |
0 |
* |
0 |
0 |
1 |
0 |
0 |
|
9 |
1 |
1 |
1 |
0 |
* |
1 |
0 |
0 |
0 |
0 |
|
10 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
11 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
12 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
13 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
Тъй
като
таблицата на
истинност е
непълна, тя
се нуждае от
следните
пояснения:
1.
Когато
към схемата
на градивния
елемент постъпва
сигнал pi+1=0
(забрана за
функциониране),
на всички
изходи
схемата
генерира
логическа
нула (pi=0, zi=0, k1=k0=0).
Всички
подобни
случаи са
обобщени в
ред №1 на
таблицата. Следващите
редове в
таблицата
поясняват случаите,
в които към
схемата на
градивния елемент
постъпва
сигнал
разрешение pi+1=1.
2.
Редове
№2, 3, 4 и 5
обобщават
случаите с
разрешение (pi+1=1)
при
положителни
числа (s=0). В ред
№2 е
представена
входна
комбинация b2b1b0
без значеща
цифра (000), а в
следващите
три реда
комбинации
със старша
значеща
цифра в три различни
позиции на
групата (001, 01*, 1**).
Необходимо е
да се поясни,
че при
положителни
числа, функциите
zi=0, тъй като
нямат
съответния
смисъл.
3.
От ред
№6 до ред №13 са
обобщени
всички
случаи на
отрицателни
числа. За
тези числа
функциите zi
имат
описания
по-горе
смисъл. Ако
входната комбинация
е (000) (ред №6) и zi-1=0,
това
означава, че
отдясно на
текущата тройка
има само нули
и тази група
следва да
генерира
само zi=1.
4.
На
изход pi се
генерира
единица само
в два случая,
при условие,
че pi+1=1:
·
При
положителни
числа (s=0) при
входна
комбинация (000),
съответстваща
на три
незначещи
цифри, без
значение на
стойността на
zi-1;
·
При
отрицателни
числа (s=1), при
входна
комбинация (111),
съответстваща
на три
незначещи
цифри, без
значение на
стойността
на zi-1.
По-горе
представената
в табличен
вид логика се
изразява
чрез
следната
система логически
функции:
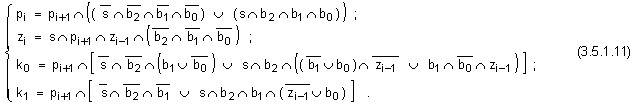
В горните
уравнения с b2 , b1 ,
b0
са означени
трите входни
бита за
текущата (№i) схема.
Накрая
остана да
представим
изходния суматор.
Според фиг. 3.5.1.1
резултатът,
който схемата
трябва да
получи, е
сумата (3.5.1.4).
Събираемите ki
в нея са
2-битови
числа. Броят r на
тези
събираеми се
определя
според (3.5.1.5). С цел
да бъде
осигурена
минимална
латентност
за
изчислението
на числото k, и
предвид
едновременното
формиране на
отделните
събираеми ki,
събирането
следва да се
осъществи
паралелно.
Пълното изследване
на задачата
за паралелно
събиране на
повече от две
цели числа е
представено
в глава 4 на
дисертацията:
http://www.tyanev.com/home.php?lang=bg&mid=17&mod=0&sub=2
Там са
формулирани
и
представени
още и допълнителни
изисквания
към задачата,
както и
нейното
обобщение.
Логическата
структура на
суматора ADD (фиг.
3.5.1.1) е
йерархична и
се синтезира
въз основа на
тривходови
концентратори
(тип 3:1). Иерархичната
структура се
определя от
дължината на
крайния резултат.
Максимално
възможната
дължина на сумата
k се
дефинира от
обща теорема,
доказана в
цитираната
дисертация.
Ако за
числата бъде
приета
типичната
дължина от 32
бита, тогава
числото k ще има
максимална
дължина от 5
бита. Върху
разрядите от
№(n-2) до №(1) следва
да се
разположат 10
градивни
елемента,
чиято
логическа
схема
реализира
системата (11).
Тези
елементи
трябва да се
свържат по начина,
показан на
фиг.3. Всяка от
тези логически
схеми ще
формира
2-битово
число ki.
Десетте
двубитови
числа
подлежат на
събиране.
Първото
ниво на
суматора (за
предложената
примерна
дължина на
разрядната
мрежа) се реализира
чрез
логическата
схема,
показана на
фигура 3.5.1.4.
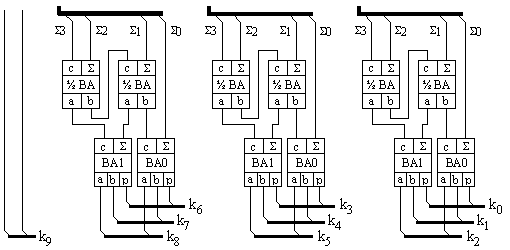
Фиг.
3.5.1.4.
Първо ниво
на суматора (3
3-входови
концентратора
за 2-битови числа)
Както
се вижда,
всеки от
тривходовите
концентратори
е реализиран
чрез два
пълни суматора
BA (Binary Adder) и
два
полусуматора ½BA.
При това
разпределение
остава едо от
числата k9,
което следва
да се подключи
към
по-високите
нива в
йерархията
на суматора.
Всеки
концентратор
от ниво С1
изчислява
4-битова сума (z3z2z1z0). Методиката,
по която се
изграждат
следващите
нива на
паралелния
суматор,
изисква разпределение
на тези 3
числа плюс
числото k9, към 3 тривходови
4-битови
концентратора.
Общата теория
и синтезът на
различни по
вид
логически схеми
на
конценратори
(3:1) е
представена
в цитираната
по-горе
дисертация и
тук не се коментира.
Концентраторите
на второто
ниво С2 ще
формират
5-битова сума.
Към получената
5-битова сума
двоичният
суматор ВА
добавя
останалото
число k9. Така се
получава
логическата
структура на
паралелния
суматор,
която е
илюстрирана на
фигура 3.5.1.5. За
удобство на
схемата е
избрано
оставеното
число да бъде
k0.
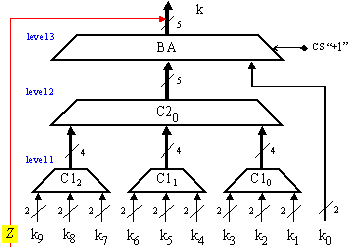
Фиг.
3.5.1.5.
Логическа
структура за
паралелното
събиране с
концентратори
3:1
На
трето ниво в
структурата
е поставен
двоичен
суматор BA.
Необходимо е
да се каже, че
неговата
логическа
схема може да
бъде
значително
опростена,
ако се отчете
фактът, че към
5-битовата
сума от второ
ниво, той
трябва да
прибави едно
2-битово
число. Това
позволява
старшите три
бита да бъдат
реализирани
чрез
полусуматори,
както това е
направено в схемите C1 от
ниво 1 (фиг. 3.5.1.4).
В
заключение
ще изложим
още някои
съображения
и обобщения.
Със синтеза
на
логическите
функции (3.5.1.11) за
схемата на
3-битовия
градивен елемент
и на
хоризонталния
паралелен
концентратор
(фиг.3.5.1.5), както и
с методиката
за декомпозиция
на
произволни
дължини на
разрядната
мрежа,
представена
в началото,
поставената
тук цел се
приема за
постигната.
Разбира се,
отделните
решения не са
единствени и
обект на
изследване
могат да бъдат
и други
различни
предложения.
Синтезираната
схема е
универсална
и адаптируема
както към
формата на
числата (цели
или дробни),
но така също
и към
машинния код,
в който те са
представени
(прав или
допълнителен).
Нещо повече
в допълнение,
че се иска
числото в
разрядната
мрежа да се
интерпретира
като число
без знак,
това
означава, че
възможните
измествания
наляво
следва да се увеличат
с единица.
Този случай
може да се реализира
апаратно
чрез
управляващ
сигнал
![]()
където с s е
означена
двоичната
цифра в
най-старшия бит
на аргумента. Така
суматорът ще
прибави
единица към
числото k. Сигналът CS(+1) се
подава по
линията на
преноса в
най-младшия
му бит, както
е показано на
фигура 3.5.1.5.
В случай, че
схемата се
прилага за
лява нормализация
на мантисата
в разрядна
мрежа с плаваща
запетая, след
изместване
на мантисата
на k
бита наляво,
е необходимо
да се
коригира стойността
на порядъка p.
Корекцията
трябва да
реализира
следната операция
![]()
при
което
нормализираната
мантиса и
коригираният
порядък ще
представят
същият
аргумент.
Полученото
число k
се използва в
програмируемите
изместващи
матрици (представени
в предходния
раздел),
които по този
начин
реализират еднотактно
изместване
на
съответния
брой разряди.
На въпроса,
колко все пак
се ускорява
изчислителният
процес след
прилагане на
описаното
еднотактно
изместване
наляво, може
да се
отговори по следния
начин.
Появата на
незначещи
цифри в
старшата
част на
числата е
обективно
явление.
Броят на тези
цифри обаче е
непредвидим,
което
означава, че
числото k има случаен
характер. За
да може да се
даде
приблизителна
числена
оценка на
поставения
по-горе въпрос,
трябва да се
знае закона
за разпределение
на тази
случайна
величина. Тук
се предполага,
че в първо
приближение
е възможно да
се приеме за
явяващите се
в разрядната
мрежа числа
равномерен
закон на
разпределение.
Тъй като
числата
всъщност
изразяват дължината
на интервала,
който заемат
в разрядната
мрежа, това
означава, че
той също е случайна
величина.
Дължината на
числото в
битове
варира в интервала
[0,
(n-2)]
като не се
имат предвид
знаковия и
най-младшия
битове. Така
средната
дължина на
числото в разрядната
мрежа се
оценява
както следва
![]()
В
същия
интервал
варира и
числото k. Тогава
неговата
средна
дължина се
оценява
аналогично
за интервала [0, (n-2)]
както следва
![]()
За
32 битова
разрядна
мрежа тази
оценка означава,
че средния
брой
измествания
наляво ще
достига до 15
бита. От своя
страна тази
стойност
позволява да
се твърди, че
схемата за еднотактно
изместване,
която ще
замести еднобитовото
последователно
изместване, води
най-вероятно
до 15-кратно
ускоряване
на тази
микрооперация.
Степента на
това ускоряване
е толкова
по-сигурна,
колкото
по-често се
налага
такова
изместване.
На
практика
законът за
разпределение
на дължината
на числата,
явяващи се в
разрядната
мрежа, а
оттам и на
дължината на
интервала,
запълнен с
незначещи
цифри, може
да бъде и
друг. Това зависи
от вида на
операциите, в
резултат на които
се получават
числата по
време на изчисления.
И накрая
възниква
въпросът
защо беше
разгледано
само
изместването
наляво?
Отговорът е
естествен
еднотактно
изместване
надясно на
повече от
един бит е
почти невъзможна
необходимост.
Единствената
ситуация, в
която се
налага
изместване
надясно с
предварително
известен
брой битове, възниква
в алгоритъма
за
целочислено
деление, в
частта му при
определяне
на остатъка
от делението.
Изграждането
на логическа
схема от
описания
по-горе вид
се
обезсмисля
по причина на
това, че
дясното
изместване
при определяне
на остатъка е
с
предварително
известен
брой битове (уравнение
(3.2.6.10б))., т.е. не
се налага
автоматичното
определяне
на числото k.
Следващият
раздел е:
3.5.2
Мултиформен,
мултиформатен
цифров
компаратор
( Multi-form, Multi-format Digital Comparator )