3.5.2 Мултиформен, мултиформатен цифров компаратор

Multi-form, Multi-format Digital Comparator

Операция сравнение Compare(X,Y), на две числа X и Y е често срещана в алгоритмите. За изпълнение на тази операция в цифровите процесори се включват съответните машинни команди, за което вече писахме в предходен раздел. Операнди x и y на тези команди са числа със знак и могат да бъдат представени в различни форми. Установяването на отношението между двете числа

цели да формира и присвои съответните истинни стойности на признаците LT (Less Than), EQ (Equal) и GT (Greater Than) според следните правила:

Операция сравнение се изпълнява в АЛУ на цифровия процесор чрез привеждане на отношението (3.5.2.1) към еквивалентното му, след представяне на операндите в инверсен машинен код (обратен или допълнителен)

Като се отчете още, че числата могат да бъдат представени в различни бройни системи, в различни машинни кодове, а така също и в различни форми и формати, с голяма увереност може да се твърди, че такова изпълнение на операция сравнение е възможно най-бавното. Освен това ще бъде необходим и достатъчно голям набор от такива машинни команди.

В същото време съществуват хардуерни структури, които съдържат в себе си като логически възли комбинационни компаратори, както и съществуват интегрални схеми, съдържащи единствено цифрови компаратори, позволяващи каскадно удължаване на разрядността на числата. В тези случаи комбинационният компаратор е синтезиран въз основа на алгоритъма за без знаково сравнение на две двоични комбинации, при което основното му достойнство е високото бързодействие.

Описаното по-долу изследване е посветено на един принципно нов подход за изграждане на многофункционални цифрови компаратори, способни на високоскоростно изпълнение на операция сравнение, чрез хардуерна реализация на операция (3.5.2.1). Многофункционалността се изразява в заложената мултиформеност и мултиформатност, позволяваща сравнението на:

1. Цели и дробни двоични числа без знак, както и такива със знак, представени в прав, в обратен или в допълнителен кодове, както и в техните модификации;

2. Цели и дробни двоично-десетични числа без знак, както и такива със знак, кодирани в код 8421, 8421⁽⁺³⁾, 4221, 2421, представени в прав, в обратен или в допълнителен кодове, както и в техните модификации;

3. Числа, представени във форма с плаваща запетая според стандарта IEEE-754.

Възможностите на такава логическа схема я определят като универсална или още като инвариантна към фόрмата и формата за представяне на сравняваните числа.

Какъвто и да е видът на представените числа, всеки от горните случаи се разпада на 4 подслучая, в зависимост от знаците им. Практически това е единственото общо нещо между изброените по-горе 3 случая. Налага се изводът, че независимо от всички останали характеристики, основавайки се на алгебрическия смисъл на числата, сравнението на знаците еднозначно определя стойностите на признаците (3.5.2.2), (3.5.2.3) и (3.5.2.4), когато те са различни както следва

Техническата реализация на сравнението на знаковите битове е облекчено от факта, че във всички форми, в които се представят числата, знаковият бит е най-левият (най-старшият) в разрядната мрежа. Веднага следва да се отбележи, че в резултат на избраната кодировка за знака на числата (0 за положителни и 1 за отрицателни), алгоритъмът на без знаковото сравнение, при сравнение на знаковите битове, ще определя признаците (3.5.2.6) на отношение (3.5.2.1) неправилно, т.е. инверсно, възприемайки знаковия бит по стойност, а не по смисъл.

В случаите, когато знаците на числата са еднакви, алгоритъмът на без знаковото сравнение ще определя признаците (3.5.2.2), (3.5.2.3) и (3.5.2.4) след сравнение на останалите битове на комбинациите, представящи числата. Това налага разглеждането на случаите по отделно, тъй като останалите битове са функция на машинния код.

Изказаните по-горе съображения обаче не са в сила за без знаковите числа, тъй като при тях старшият бит трябва да се възприема по стойност. Това налага предварително инициализиране на този случай, тъй като е изключение от го горните правила.

Случай А) Двоични числа

Когато числата имат знак, за тяхното машинно представяне се използва обратен или допълнителен код, за получаването на които е необходим прав код. За n-битова разрядна мрежа с дясно фиксирана запетая тези кодове се дефинират така

където чрез n е означена дължината на мултиформатната разрядна мрежа. Различните формати са възможни благодарение на правилото за знаково разширение на числата.

Аналогична зависимост дефинира инверсните кодове и за двоичните числа с ляво фиксирана запетая.

В първия случай на (3.5.2.7), когато и двете числа са положителни, отношението на двата инверсни кода

е еквивалентно на отношение (3.5.2.1) и може да се изчисли чрез алгоритъма на без знаковото сравнение.

Във втория случай на (3.5.2.7), когато и двете цели числа са отрицателни, отношението на двата инверсни кода се изразява съответно чрез отношението на числата

което очевидно също е еквивалентно на (3.5.2.1) и за двата кода, тъй като по-малкият модул ще генерира по-голяма по стойност разлика.

Налага се обобщението, че алгоритъмът на без знаковото сравнение може да се използва за сравняване както на числа без знак, така и на числа със знак, представени в инверсни машинни кодове, включително и модифицирани такива, които имат по 2 знакови бита. Това важи и за числата с ляво фиксирана запетая, както и за числата, структурирани с цяла и дробна част. С други думи положението на запетаята е без значение, тъй като тук се имат предвид само числа, представени в позиционни бройни системи.

Когато сравняваните числа са представени в прав или в обратен код, се налага предварително автоматично разпознаване и игнориране на знаковите нули (+0, -0), едно различие, което има място в тези два кода. Това лесно може да бъде осигурено с хардуерни средства.

Специален коментар заслужава сравнението на числа представени в прав код, който за цели числа се дефинира както следва

В първия случай на (3.5.2.9), когато и двете числа са положителни, отношението на двата кода

е еквивалентно на отношение (3.5.2.1) и може да се изчисли чрез алгоритъма на без знаковото сравнение, тъй като то всъщност представлява отношението

.

Във втория случай на (3.5.2.9), когато и двете цели числа са отрицателни, отношението на двата кода се изразява съответно чрез отношението на числата

което очевидно се решава чрез отношението │X│¤│Y│. В резултат на това признаците се определят вярно, само когато модулите са равни. При различни модули в този случай, стойностите на признаците LT и GT, се определят неправилно – техните правилни стойности са инверсни. Изключенията, което генерират числата със знак обаче могат да бъдат дешифрирани и всички възможни случаи да бъдат обобщени от следната логическа функция

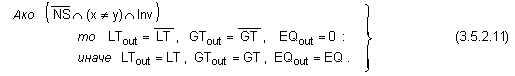
където с Inv (inversion) е означена логическата функция

а с индекс out са означени крайните изходни за компаратора стойности на признаците.

Както се вижда от (3.5.2.11) и (3.5.2.12), за идентификация на всички изключения, логическата схема на компаратора е функция от два допълнителни сигнала:

1. Сигнал NS (Not Signed numbers), деклариращ, че числата са без знак;

2. Сигнал RC (Right Code), деклариращ, че числата са представени в прав код.

Случай Б) Двоично-десетични числа

Десетичните числа се представят като наредена последователност от кодовите комбинации на своите десетични цифри – (8421), (8421⁽⁺³⁾), (2421) и др. Най-широко се прилага първият от посочените. Машинните кодове на цели числа със знак се дефинират така

където с q е означена основата на бройната система, в която е представено числото, като в частност тук се има предвид q=10. С n отново е изразена дължината на мултиформатната разрядна мрежа. За всеки 2/10-чен код е известна алгоритмична схема за постигане на зависимостта (3.5.2.13), която изхожда от техния прав код. Както и за двоичните числа, знаковите нули в прав или в обратен код следва предварително да бъдат дешифрирани и уеднаквени.

Прилагането на алгоритъма на без знаково сравнение за проверка на отношението

на 2/10-чни числа напълно съответства на зависимостите (3.5.2.2, -3, -4 и -6). При изпълнение на този циклически алгоритъм, на сравнение се подлагат две цифри в текущия i-ти десетичен разряд

dx_i * dy_i ?

Тъй като тези цифри са представени с двоични комбинации, това отношение се проверява бит по бит по силата на алгоритъма на двоичното без знаково сравнение. От това следва, че отношението за тези две цифри ще бъде вярно, ако за техния 2/10-чен код е в сила свойството монотонност. Това свойство е в сила и за кодовите комбинации на десетичните цифри в инверсни машинни кодове на числата със знак. От тук следва окончателният извод, че алгоритъма на двоичното без знаково сравнение може да се приложи и върху различно кодирани 2/10-чни числа. Алгоритъмът е инвариантен към положението на запетаята на числата.

Правият код на 2/10-чните числа се дефинира както следва

Всичко казано преди това за сравнението на двоичните числа в прав код, е в сила и за 2/10-чните числа в прав код. Ето защо логическата функция (3.5.2.11) е в сила и за тези числа. Следва, че тя е инвариантна към основата на бройната система, в която са представени числата.

Случай В) Числа във форма с плаваща запетая

Разглежда се структура на разрядната мрежа според стандарта IEEE-754 с техника на скрития бит, имаща вида, представен на фигура 3.5.2.1.

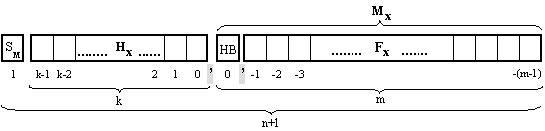
Фиг. 3.5.2.1. Структура на разрядната мрежа

в която означенията са:

S_M – знаков бит на мантисата (на числото);

H_X – характеристика. За характеристиката са в сила следните зависимости:

HB – скрит бит;

M_X – нормализирана мантиса. Има вида: M_X = (1,F_X);

F_X – фракция.

Мултиформатността се осигурява от променящите се дължини k (8, 11 или 15 бита) и m (23, 52 или 64 бита), дефинирани от стандарта.

Мантисата е число със знак и се представя в прав код. Това означава, че отношението (3.5.2.1) може да бъде определено чрез алгоритъма на без знаковото сравняване. Това отношение обаче следва да бъде съобразено с характеристиките на числата. Характеристиките се възприемат като числа без знак и по стойност също могат да се сравнят чрез алгоритъма на без знаковото сравняване. Тяхното отношение обаче трябва да се приложи върху стойностите на порядъците, които са числа със знак.

Според (3.5.2.15) отношението (H_x)*(H_y) се разглежда във вида

който може да бъде сведен до

Последното отношение обаче не винаги е еквивалентно на отношението на характеристиките, тъй като порядъците са числа със знак, а те могат да се случват в 4 различни комбинации.

Комбинациите от различни знаци съответстват на правилно определено чрез сравняване на характеристиките отношение, тъй като отрицателният порядък води до операция изваждане (виж (3.5.2.15)), което силно отдалечава по стойност съответната характеристика от другата. В случай, че знаците са положителни, отношението на характеристиките е в пълно съответствие с отношение (3.5.2.17). В последния случай, когато знаците на порядъците са отрицателни, в резултат на операция изваждане, отношение (3.5.2.17) също в съответствие с отношение (3.5.2.16). В случай на две отрицателни числа, по-голямо е числото с по-малкия порядък.

Сравнението на мантисите, като числа със знак, представени в прав код, напълно съответства на казаното вече за числата с фиксирана запетая. Тъй като при тези условия сравнението генерира същите изключения, следва да се приложи логиката на функция (3.5.2.11).

Логическа схема на компаратора

Логическата схема на компаратора е синтезирана в съответствие с алгоритъма за без знаковото сравнение и представлява последователност от еднобитови компаратори. Принципната логическа схема за всички средни i-ти разряди

е представена на фигура 3.5.2.2. Логическите функции на компаратора за тези разряди са синтезирани според известна от литературата методика и имат вида:

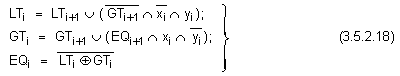
Тяхната реализация води до следната логическа схема:

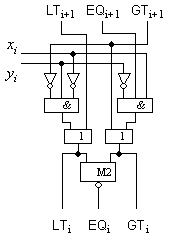
Фиг. 3.5.2.2. Логическа схема на i-тия бит

Логическата схема на компаратора в най-старшия (n-1)-ви разряд (по-долу на фигура 3.5.2.3) е синтезирана като функция и от инициализиращите сигнали NS и RC, определени по-горе в края на случай А). По този начин, когато числата генерират описаните изключения и изходните признаци трябва да се инвертират, в този разряд се генерира разрешението E (Enable), което се използва в най-младшия (нулевия) разряд на компаратора. Логическите функции на компаратора за този разряд са следните:

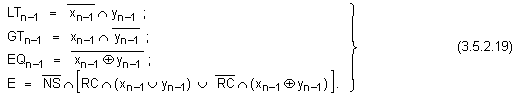
Тяхната реализация води до следната логическа схема:

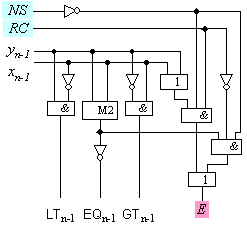
Фиг. 3.5.2.3. Логическа схема на старшия бит

Изключенията, които генерират числата със знак в прав и в допълнителен код, могат да бъдат игнорирани, ако знаковите битове на числата бъдат инвертирани преди сравнение. С други думи, предварителната инверсия на знаковите битове заменя смисъла на кодовите цифри на знаците с числена стойност, водеща до правилно определяне на признаците. Така при сравнение на числа, представени в инверсни машинни кодове, не се генерират изключения. Изключение се генерира единствено при две отрицателни числа, представени в прав код. Логиката за дешифриране на това изключение е представена от функция (3.5.2.11), в която обаче следва да се използва следната логическа функция

Логическата схема на компаратора в най-старшия (n-1)-ви разряд (фигура 3.5.2.4) е синтезирана аналогично, но при отчитане на зависимостта (3.5.2.20) за инициализиращия сигнал Inv. Логическите функции на компаратора за този разряд са следните:

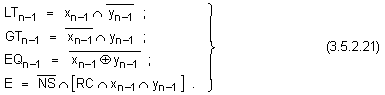
Логическата схемата в този втори вариант е следната

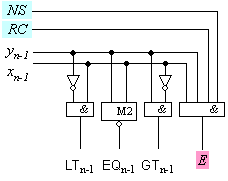
Фиг. 3.5.2.4. Логическа схема на старшия бит (с предварителна инверсия на знака)

Очевиден е изводът, че апаратната реализация на уравненията (3.5.2.21) е по-икономична в сравнение с тази на (3.5.2.19).

Логическата схема на компаратора в най-младшия нулев (0) разряд е представена на фигура 3.5.2.5. Както се вижда, изходните стойности на признаците са функция от разрешението Е, чиято логика е следната

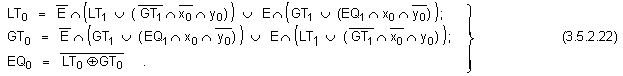
Разрешението влияе на окончателните резултати само в случай, че числата са във форма с плаваща запетая и са отрицателни и не са напълно еднакви.

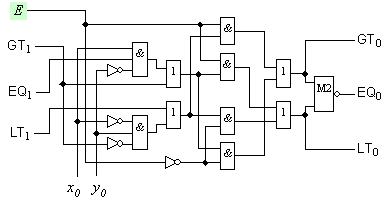
Фиг. 3.5.2.5. Логическа схема на младшия бит

Заключение

Синтезът на цифров компаратор с множеството различни характеристики се оказва възможен. Синтезираната логическа схема прилага последователно сравнение, но може да бъде преструктурирана чрез каскадни подходи, описани в литературата.

Чрез входния сигнал NS схемата различава числата без знак от числата със знак.

Схемата е мултиформатна, тъй като е инвариантна към дължината на разрядната мрежа, в която са представени числата. Това се дължи на свойствата на машинните кодове.

Схемата е мултиформена, защото е инвариантна към запетаята на числа, когато те са представени в позиционни бройни системи. Тя е инвариантна още към различните машинни кодове и техните модификации.

Схемата е инвариантна още към кода за представяне на десетичните цифри, стига той да притежава свойството монотонност.

Схемата проявява своите универсални възможности и върху числа представени във форма с плаваща запетая според стандарта IEEE-754. Както и във форма с фиксирана запетая, за получаване на верните стойности на признаците, се използва допълнителния инициализиращ сигнал RC. Логическите елементи, необходими за реализация на функцията на този сигнал, увеличава апаратните разходи нищожно. Те не влияят на латентността на схемата. Мултиформатността на схемата е в сила и върху числата с плаваща запетая благодарение на адитивната функционалност (3.5.2.13), според която е дефинирана характеристиката на числата.

Времето за превключване на цифровия компаратор е функция от самите числа, ето защо то е променлива величина, която има случаен характер и геометрично разпределение. Статистическите резултати налагат обобщението, че в рамките на допустимото ниво на значимост за критерия на Пирсон, очакваното време за превключване на компаратора е в границите на 1/3 от неговата дължина. Тези числени оценки могат да послужат за статистическа оценка на производителността на тук предложеното микроконвейерно звено, работещо в условията на асинхронно управление, за което читателят може да прочете в книга [5].

За да подкрепим изложените обобщения и подпомогнем усвояването на схемата на компаратора, по-долу са представени няколко числени примера.

ПРИМЕР 1. Сравнение на двоични числа с ФЗ.

X = -16 , Y = -19 , n=8 [b]

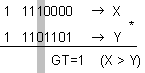
В прав код на числата същият пример има вида

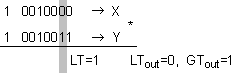
ПРИМЕР 2. Сравнение на 2/10-чни числа, представени в код BCD:8421.

X = -6170 , Y = -3369 , n=5 [pos.] , LT=1.

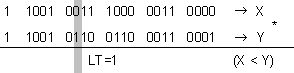
В прав код на числата същият пример има вида

,

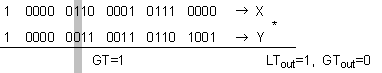
ПРИМЕР 3. Сравнение на числа, представени във форма с ПЗ.

Числените примери са за 4-те знакови комбинации на числата в отношението X*Y:

Пример 3.1.

Благодарение на знаците в този случай се получава признак GT=1 ( X>0, Y<0 ).

Пример 3.2.

Благодарение на знаците в този случай се получава признак LT=1 ( X<0, Y>0 .

Пример 3.3.

В този случай знаците на числата са еднакви и сравнението се пренася върху старшите битове на характеристиките. Тъй като p_x<0, старшият бит на характеристиката H_x ще съдържа нула, т.е. H_x[k-1]=0. В същото време p_y>0. Това означава, че старшият бит на характеристиката H_y ще съдържа единица, т.е. H_y[k-1]=1. В резултат от сравнението на старшите битове на характеристиките за отношението на числата ще бъде определен признак LT=1, т.е. 0,00005 < 600.

Пример 3.4.

В този случай знаците на числата са отново еднакви и характеристиките са същите, както в предходния пример. Сравнявайки ги отново ще се получи същия признак LT=1, което за характеристиките е вярно, но за числата като цяло не е вярно, тъй като отчитайки знаците, съотношението е

-0,00005 > -600.

В този случай правилните стойности на признаците LT и GT са инверсните.

Изключението, което се изявява в работата на компаратора във втория случай, разкрито по-горе, се дължи на факта, че мантисите на числата са представени в прав код. Това неизбежно изисква предварителна инициализация на логическата схема. Тази инициализация може да бъде реализирана с вече предложения по-горе сигнал RC. Стойностите на изходните признаци се определят от функция (3.5.2.9).

Следващият раздел е:

§ 3.6 Операции за преобразуване на числата от една в друга бройна система

( Converting numbers from one number to another notation )