§ 3.6 Операции за преобразуване на числата от една в друга бройна система

Converting numbers from one number to another notation

Ще се спрем само на преобразуванията между десетичната и двоичната бройни системи, които са актуални за разглеждания тук структурен аспект.

Ще обърнем внимание, че тези преобразувания се изпълняват върху модулите на числата, а те съществуват в явен вид само в правия им код, т.е. тук ще предполагаме, че числата в качеството си на операнди, са вече изобразени в прав код. Ясно е, че знакът на търсения еквивалент се присвоява от знака на изходното число.

Операциите за преобразуване на числата от десетична в двоична бройна система и обратно са неизбежни във всеки компютър по очевидни причини. Обикновено те не са включени в състава на изпълнимите операции и се осигуряват с чисто програмни средства, но алгоритмите, по които практически се осъществяват, както и възможностите за тяхната апаратна реализация представляват интерес. Ще бъдат разгледани машинните алгоритми за преобразуване както на числа с дясно фиксирана запетая, така и с ляво фиксирана запетая, които се различават от изложените тук в глава 1, пункт 1.1.2.

А) Преобразуване на числа с ДФЗ от десетична в двоична бройна система

След въвеждане на изходното десетично число, примерно от клавиатурата, като символен низ от ASCII кодови комбинации, и след подходяща обработка, същото се оказва представено в 2/10-чна бройна система (в код 8421) в пакетиран формат, т.е. като наредена последователност (кортеж) от вида (1.1.3). Алгоритъмът на преобразуването му се извлича от полинома на числото, записан по схемата на Хорнер. Например 5-разрядното десетично число Х,

където с d_i, i=0,1,2,3,4 са означени десетичните цифри, представлява следния полином от 4-та степен (m-1)=4:

който в схемата на Хорнер има вида:

Тази схема е забележителна със следното: първо, в нея е очевидно циклическото повторение на две действия - събиране и умножение; второ, умножението се извършва с един и същ множител - основата на бройната система q=10.

Твърди се, че ако всички елементи в схемата на Хорнер (3.6.1) се представят в двоична бройна система и ако всички означени действия се изпълнят по правилата на тази бройна система, то резултатът ще бъде търсеният двоичен еквивалент. Необходимо е да се отбележи, че това преобразование е винаги точно (виж пункт 1.1.2). Ще споменем любопитния факт, че този алгоритъм е синтезиран от Нютон през 1719 година, а Хорнер се е позовал на него в една своя статия цели 100 години по-късно (през 1819 година). Обобщеният алгоритъм е изложен от Доналд Кнут в том 2 (“Seminumerical algorithms”) на книгата му “The art of computer programming”, (1969).

Вече е ясно, че алгоритъмът за това преобразуване е циклически - повторенията ще бъдат толкова, колкото са цифрите на изходното десетично число. Ако се приеме, че това число е m-разрядно, то рекурентната формула в следната схема

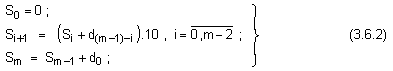
изразява натрупването в променливата S стойността на търсения еквивалент като двоична сума.

Ще предложим логическа структура на устройство за апаратна реализация на изказания алгоритъм. Като имаме предвид натрупването на сумата според (3.6.2), логическата структура е удобно да бъде построена на базата на натрупващ суматор – вижте фигура 3.6.1.

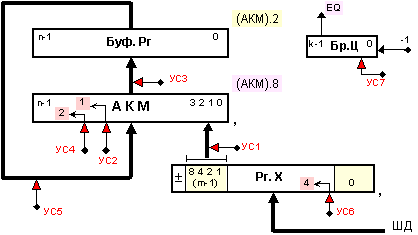
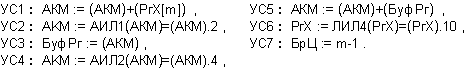
Фиг. 3.6.1. Примерна логическа структура на устройство за преобразуване

на числа с ДФЗ от 10-чна в 2-чна бройна система

Както се вижда, в логическата структура има двоичен натрупващ суматор АКМ, регистър за операнда РгХ, допълнителна памет в лицето на БуфРг и един изваждащ брояч БрЦ. В изходно състояние акумулаторът е нулиран, модулът на десетичното число е зареден в РгХ, а броячът е установен в начално състояние и съдържа числото (m-1). Цифрите на операнда се подават за натрупване в акумулатора със старшите напред, ред който е определен от схемата на Хорнер и изразен чрез (3.6.2). Това налага регистърът на десетичното число РгХ да бъде изместващ на един десетичен разряд наляво.

Структурата функционира така: след натрупване на поредната тетрада към междинната сума в акумулатора по УС1, се извършва умножението с множителя 10. Последното е реализирано чрез разлагане на множителя във вид на сума: 10=8+2=2³+2¹. Тази сума позволява да се реализира умножението (АКМ).10 по косвен път - чрез съответните двоични измествания на един и на три бита. След първото изместване на един бит по УС2, съдържанието на акумулатора, представляващо числото (АКМ).2, временно се запомня в буферния регистър – по УС3. Следва още едно изместване на съдържанието на акумулатора, този път на 2 бита наляво – УС4, с което общото изместване става на 3 бита и съдържанието му приема стойността (АКМ).8. Към тази стойност по УС5 се прибавя съдържащата се в буферния регистър, при което в акумулатора се получава стойността (АКМ).10.

По време на празния такт на акумулатора поредното натрупване се отброява в БрЦ, чрез изваждане на единица. По същото време чрез УС6 може да се извърши изместване във входния регистър на един 10-чен разряд, т.е. на 4 бита едновременно. В края на тази последователност се проверява условието за край на цикъла – дали не се е появил флагът EQ≡{(БрЦ)=0} . Ако не, т.е. EQ=0, то следва повторение на горе описаните действия - събиране с поредната тетрада, умножение с 10, изместване във входния регистър, отброяване и пак проверка. Ако да, т.е EQ=1, това е краят на циклическите повторения и към съдържанието на акумулатора остава да се добави само най-младшата тетрада, останала във входния регистър. Така в крайна сметка резултатът се получава и остава в акумулатора.

Необходимо е да обърнем внимание, че за разлика от пълноразрядното събиране с операнда, подаван с управляващ сигнал УС5, събирането по УС1 с текущата десетична цифра (тетрада) е пълноценно само в младшите 4 бита.

За да може да бъде получен двоичният еквивалент на всяко m-разрядно десетично число, следва дължината на двоичните възли (акумулатор и буферен регистър) да бъде достатъчна, в противен случай ще се получи препълване в двоичното поле. За тази цел е необходимо да се приложи определението (1.1.3.1), според което двоичната дължина от n бита ще бъде:

или

От полученото отношение се вижда, че дължината на двоичното поле от n бита, е 3,3222591 пъти по-голяма от дължината m на десетичното поле, или с други думи един десетичен разряд е еквивалентен на 3,3222591 двоични разряда. Така можем да твърдим например, че 19 десетични разряда ще са еквивалентни на 64 двоични, тъй като:

19.(3,3222591) ≈ 64 [b] ,

а 7 десетични разряда - на 24 двоични. Препоръчваме на читателя да запомни отношенията:

24 ↔ 7 ; 64 ↔ 19 ,

тъй като те имат връзка с определянето на необходимата (на максималната) дължина на числовите текстови полета (имаме предвид програмните езици и форматните спецификатори за числените стойности).

Използуваното по-горе разложение на множителя 10 в схемата на Хорнер (3.6.1) не е единственото, което може да бъде приложено. Същият резултат може да се получи и при следното разложение

10 = (4 + 1).2 ,

което води към следната последователност от микрооперации:

· Запомняне на съдържанието на акумулатора в буферния регистър;

· Изместване на два разряда наляво на съдържанието на акумулатора;

· Събиране на съдържанието на акумулатора с това на буферния регистър;

· Изместване на един разряд наляво на съдържанието на акумулатора.

Читателят може сам да изрази предпочитание към съответната схема в случай на необходимост, когато трябва да постигне съответно бързодействие или да използува по подходящ начин съществуващи в структурата възли и връзки.

Б) Преобразуване на числа с ЛФЗ от десетична в двоична бройна система

Според изложеното в пункт 1.1.2, за това преобразувание може да се използва следния алгоритъм: изходното десетично число, представено в 2/10-чна бройна система (в код 8421) в пакетиран формат (m цифри), се умножава последователно с основата на бройната система, в която трябва да се изобрази, т.е. с числото 2. Цялата част на така получаваните междинни произведения представлява всяка поредна цифра на търсения двоичен еквивалент. Редът, в който се получават двоичните цифри, е низходящ - от най-старшата към най-младшата. За разлика от предидущото преобразувание, преобразуванието на дробните десетични числа е не винаги точно (виж пункт 1.1.2), ето защо според алгоритъма, последователните умножения трябва да бъдат прекратени, когато се получи нулево междинно произведение, или когато търсеният двоичен еквивалент се изобрази с достатъчно висока степен на точност, но не по-ниска от тази на изходното число.

Според изказания алгоритъм, става дума за циклически действия, които се повтарят най-общо толкова пъти, колкото е двоичната дължина n[b] на търсения еквивалент, т.е. n пъти. Според зависимостта (3.6.3), тя се определя от десетичната дължина на изходното число – в общия случай m разряда. В този алгоритъм броячът на циклите, с чиято помощ ще се организира повторението, ще трябва да приема за начална стойност двоичната дължина, т.е. числото n.

Последното, на което трябва да се обърне внимание, е реализацията на операция умножение на 2/10-ните числа с числото 2. Умножението с числото 2 се изпълнява по определение, т.е. чрез събиране на множимото само със себе си: Х.2 = Х+Х. Подобни повтарящи се събирания могат да се организират в един натрупващ 2/10-чен суматор с помощта на буферен регистър. В резултат на изложеното лесно се синтезира логическата структура на устройство за преобразуване, показана на фигура 3.6.2.

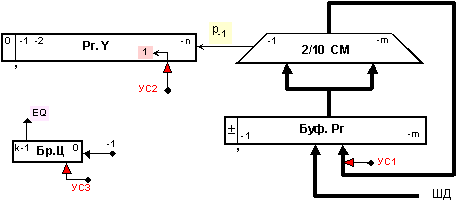
УC1 : БуфРг := СМ , УС2 : РгY := ЛИЛ1(РгY) , УС3 : БрЦ := n .

Фиг. 3.6.2. Примерна логическа структура на устройство за преобразуване

на числа с ЛФЗ от 10-чна в 2-чна бройна система

От фигурата се вижда, че стойността на преноса p_-1 от най-левия разряд на суматора, в качеството на най-старша цифра на сумата (т.е. на цялата й част), се приема в изместващия регистър РгY, в качеството му на поредна двоична цифра. След всяко събиране от брояча БрЦ се изважда единица, а в буферния регистър се запомня само дробната част на сумата. Резултатът се получава в РгY.

Необходимо е да предупредим читателя, че изпълнението на алгоритъма може да бъде ускорено като се следи за нулево междинно произведение. Нулевото междинно произведение всъщност е причина за преждевременно прекратяване на горе описаните повтарящи се микрооперации. В този случай, допълването до окончателната дължина на търсения еквивалент, имащ вида 0,zz…zz00…0 , с незначещи младши цифри нула, не променя неговата стойност.

В) Преобразуване на числа с ДФЗ от двоична в десетична бройна система

Алгоритъмът на това преобразувание е аналогичен на този, изложен в пункт А). Изходното цяло двоично число, например 5-разрядното

където с b_i, i=0,1,2,3,4 са означени двоичните цифри, преставлява следния полином от 4-та степен:

чиято схема на Хорнер има вида:

Твърди се, че ако всички елементи в тази схема се интерпретират като десетични и ако всички означени в (3.6.4) действия се изпълнят според правилата на десетичната бройна система, ще се получи търсеният десетичен еквивалент. Това преобразувание е винаги точно (виж пункт 1.1.2).

Ако изходното двоично число има дължина от n[b], то неговият десетичен еквивалент ще има десетичната дължина от m десетични разряда:

Както и в предидущите логически структури, така и тук, зависимостта (3.6.5) служи за определяне на дължината на необходимите възли. Така например, в случая е необходим 2/10-чен суматор за извършване на натрупването на цифрите b_i, интерпретирани като десетични, а така също и за реализиране на удвояването на междинните суми по схемата Х.2 = Х+Х. Алгоритъмът, описващ тези действия, е циклически, от вида с предварително известен брой повторения и за неговото реализиране е необходим брояч, чиято начална стойност трябва да бъде числото (n-1). Една примерна логическа структура за реализация на това преобразувание е показана на фигура 3.6.3.

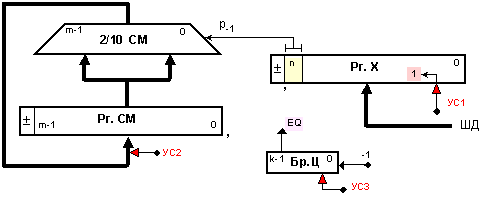
УC1 : РгХ := ЛИЛ1(РгХ) , УС2 : РгСМ := СМ , УС3 : БрЦ := n-1 .

Фиг. 3.6.3. Примерна логическа структура на устройство за преобразуване

на числа с ДФЗ от 2-чна в 10-чна бройна система

Както може да се види, комбинационният двоично-десетичен суматор позволява да се съвмести натрупването с удвояването. Цифрите на изходното число се подават със старшите напред по входа на най-младшия пренос на суматора.

В структурата от фигура 3.6.3 са изобразени само най-необходимите управляващи сигнали.

Г) Преобразуване на числа с ЛФЗ от двоична в десетична бройна система

Преобразуването на дробните числа (с ляво фиксирана запетая) в десетична бройна система обикновено извършваме по степените на основата 2. Това е свързано с определяне на съответната реципрочна стойност, което от своя страна е затруднително и този алгоритъм на намира машинна реализация. Тук се предлага да се използва основата на десетичната бройна система, но да се изпълняват двоични операции.

Алгоритъмът за това преобразуване представлява последователно умножение на двоичното число с основата на бройната система, в която то преминава, т.е. с числото 10. Умножението с числото 10 се осъществява по начините, описани в точка А). Тъй като това умножение е свързано с изместване наляво на един и три разряда, получената двоична сума (Х.2 + Х.8) се разширява с четири двоични разряда вляво от запетаята – 3 бита от изместването и 1 бит от евентуален пренос вследствие събирането. Тези двоични разряди формират цялата част на посочената сума. Тази цяла част не може да надхвърли по стойност числото 9, т.е. за десетичната бройна система тя е елементарно количество и следователно може бъде разглеждана като двоично кодирана десетична цифра в тегловно значимия код 8421. С други думи, след всяко умножение на дробната част, двоичната тетрада в цялата част на произведението се отнема в качеството й на поредна 2/10-чна цифра на търсения еквивалент. По този начин цифрите на търсения еквивалент се получават в низходящ ред, т.е. със старшите напред. Това преобразувание е винаги точно (виж пункт 1.1.2), и за него е необходимо съотношението

където n е дължината на двоичното число в [b], а m е броят на неизвестните цифри на десетичния еквивалент. Циклическото повторение на микрооперациите изместване и събиране се организира в логическата структура чрез изваждащ брояч, чиято начална стойност е числото m. Устройството за това преобразуване, показано на фигура 3.6.4, се реализира удобно чрез двоичен натрупващ суматор.

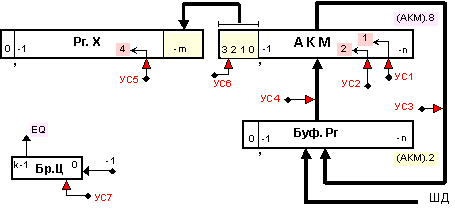
Фиг. 3.6.4. Примерна логическа структура на устройство за преобразуване

на числа с ЛФЗ от 2-чна в 10-чна бройна система

Изходното двоично число първоначално се приема в буферния регистър, откъдето чрез управляващия сигнал УС4 се изпраща в акумулатора. Там чрез УС1 се измества на един разряд наляво и полученото (X.2) по УС3 се запомня в обратно в буферния регистър. С това изходното число престава да съществува. След това по УС2 съдържанието на акумулатора допълнително се измества на още 2 разряда, при което в него се получава произведението (X.2).4=X.8. Чрез УС4 в акумулатора постъпва числото (X.2). Получава се сумата (X.8+X.2), в резултат на което, в цялата й част (разряди 3,2,1,0 на акумулатора) се формира текущата тетрада на десетичния еквивалент. С изместване на съдържанието на РгХ по УС5, в него се приема така получената в акумулатора 2/10-на цифра. След това чрез УС6 цялата част на сумата се нулира: АКМ[3…0]=0. На това поредният цикъл завършва, той се отброява в брояча на цифрите и ако все още не са получени всички цифри, т.е. флагът не е вдигнат (EQ=0), процедурата се повтаря върху останалата в акумулатора дробна част на текущото произведение.

В заключение трябва да добавим, че описаните по-горе в точки А), Б), В) и Г) алгоритми, изискват числата да са представени в прав код, тъй като се обработват техните модули. За целта в логическите структури е необходимо временно съхраняване на знака на числото. В последствие, той се присвоява на получения еквивалент.

Представените алгоритми се наричат машинни и са илюстрирани с множество числени примери в книга [2].

Следващият раздел е:

§ 3.7 Преобразуване на фòрмата и формáта за представяне на числата

( Conversion forms and formats of presentation the numbers )