§ 3.7 Преобразуване на фòрмата и формáта за представяне на числата

Conversion forms and formats of presentation the numbers

Още в началото искаме да предупредим читателя за това, че изписването на две от думите в заглавието на темата е еднакво и това ни създава определени затруднения. Смисълът, който се има предвид в конкретния текст, става напълно ясен от ударението в съответната дума. Явното указване на ударението обаче е неудобно да се прави непрекъснато, така че по-долу в текста ние в голяма степен разчитаме на интелигентността на читателя, както и на неговата концентрация.

1. Преобразуване на фòрмата на числата

Преобразуване на числата от форма с фиксирана запетая (ФЗ), (ДФЗ, ЛФЗ) във форма с плаваща запетая (ПЗ) и обратно се налага да се извършва във всеки алгоритъм. Почти във всеки алгебрически израз, когато се съчетават променливи и константи, обявени от програмиста с различни типове, се налага уоеднаквяване по форма и по формат на всяка двойка операнди. Това се налага, тъй като всяко аритметично-логическо устройство реализира алгоритмите на аритметическите операции между два еднакви по форма и по формат операнда. В това читателят навярно вече е убеден, след като бяха представени множество логически структури на такива устройства. Няма как да бъде извършена например операция събиране, ако единият от аперандите е от тип Integer, а другият от тип Float (Real). Нещо повече, възниква въпросът кой в кого да се преобразува – цялото в реално или реалното в цяло? В този конкретен пример, за да не се загуби точността на реалното число, се преобразува цялото в реално. Едва след това се изпълнява основната операция събиране. В програмните езици по тези причини се въвежда ранг или приоритет между основните изпълними операции. Обратното преобразование, реално в цяло, е възможно да се наложи в оператор за присвояване, когато на променлива от тип Integer се налага да се присвои реална стойност.

Реализирането на тези преобразувания може да бъде осъществено както програмно, така и машинно чрез включването им в системата машинни команди като изпълними операции. На читателя ще се наложи да използува или да интерпретира по подходящ начин тези преобразувания най-вероятно при програмиране на алгоритмичен език от високо ниво и тъй като ефектите от тези преобразувания са изключително важни, това ги прави актуални за нас. Подценяването на тази тема може да донесе на програмиста сериозни неприятности, ето защо неговата отговорност е голяма.

А) Преобразуване на двоични числа с фиксирана запетая в двоични с плаваща запетая

Ще имаме предвид числа с дясно фиксирана запетая (вижте фигура 1.1.6.1.3), както и една и съща дължина от n[b] на разрядната мрежа и за двете форми. Алгоритъмът на това преобразуване изисква изходното число да бъде представено в прав код. Тъй като числата с фиксирана запетая най-често се представят в допълнителен код, налага се той да се преобразува в прав, който както знаем съдържа модула на числото. Значещата част на числото, намираща се в разрядната мрежа, следва да се превърне в нормализирана мантиса. За целта цялото число трябва да се нормализира спрямо левия край на разрядната мрежа. Лявата нормализация може да се изпълни и върху допълнителния код на числото, което изисква повече апаратура. Проблемите и начина на изпълнение на лявата нормализация и в двата кода бяха вече описани в пункт 3.2.8.

Освен постигането на условието (1.1.6.2.2) за нормализиран вид на мантисата, в процеса на нормализация следва да се определи и порядъкът на числото. За сега при следващите обяснения тук ще имаме предвид структурата на разрядната мрежа с плаваща запетая (вижте фигура 1.1.6.2.2), която за удобство представяме по-долу.

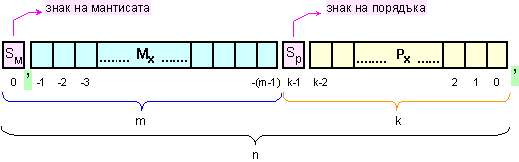
Фиг. 3.7.1. Структура без изместен порядък

Нека си представим числото Х в разрядната мрежа с фиксирана запетая по следния начин:

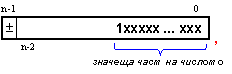
Изместването на числото Х наляво до вида

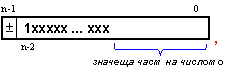
го превръща в полином от (n-2)-ри ред. Ако се приеме, че редът на полинома на изходното число е k, където k<(n-2), то нормализираният вид на числото се получава след [(n-2)-k] на брой едноразрядни измествания наляво, т.е.

Тъй като редътна полинома на изходното число k е неизвестен, необходимо е в процеса на нормализиране да бъдат преброени изместванията наляво. Ако броят на изместванията се означи с h, то уравнението:

(n-2) - k = h (3.7.1)

е уравнение с едно неизвестно - k. Неговото решение е:

k = (n-2) - h

и тъй като порядъкът на числото 1 е +1, то окончателният израз за порядъка на числото ще бъде:

В крайна сметка числото Х ще има вида:

Когато дължината на разрядната мрежа с дясно фиксирана запетая е по-голяма от дължината на полето на мантисата (има се предвид, че общата дължина n на разрядната мрежа с фиксирана запетая е равна на тази с плаваща запетая),

(n-1) > (m-1) (3.7.3)

е възможно някои числа да не се изобразяват във форма с плаваща запетая точно, тъй като поради по-малката дължина на полето за мантиса, ще бъдат отрязани (загубени) младшите им разряди. Възможно е загуба на един, на два или на повече разряди, но не повече от (n-m). За да се намали грешката, може да бъде изпълнено закръгляне на мантисата. Така например, ако n=32[b], преобразуването на едно цяло число в число с плаваща запетая и формат SP, ще има мантиса от 23 цифри. Така превръщайки се в мантиса цялото число може да загуби до 8 младши цифри. Абсолютната стойност на максималната загуба в този случай представляват 255 единици. Ако се направи обратно преобразуване отпечатъкът (стойността) на числото няма да бъде същият. Тази загуба на информация е неизбежна и следва да се разбира от програмиста, за да употребява и преобразува типовете на данните правилно.

Неизвестният порядък p_x се определя апаратно в процеса на нормализиране с помощта на изваждащ брояч, реализирайки по този начин уравнение (3.7.2). Началната стойност на брояча следва да бъде (n-1). Полученото крайно съдържание в този брояч, се записва като окончателна стойност на порядъка в полето за порядък от разрядната мрежа.

В края на обясненията ще споменем и изключителния случай, когато изходното число е числото X_min. За това число описаното правило не е в сила. Това е единственото число, което в този алгоритъм прави изключение. Лявата нормализация на това число, имащо модул с n-разрядното двоично изображение (100...0), изисква едно изместване надясно, за да се получи мантиса от вида

Порядъкът на това число се получава по същия начин, но тогава h=-1, т.е. отрицателно, тъй като посоката на изместването е обратна, т.е.

В случай, че формата с плаваща запетая използува техниката на "скрития бит", лявата нормализация изисква намаление на порядъка с единица, а описаното по-горе изключение вече няма да бъде изключение.

Основните елементи в структурата на разрядната мрежа с изместен порядък (вижте фигура 1.1.6.2.3) ), която за удобство представяме по-долу, са разместени, а вместо порядък трябва да се представи характеристиката H_x.

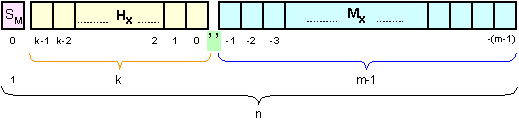
Фиг. 3.7.2. Структура с изместен порядък

Характеристиката, както е известно се определя според (1.1.6.2.17) така

а при използване на техниката на скрития бит така

откъдето следва и съответното управление на брояча, който ще формира стойността й в процеса на нормализация на мантисата. Тя, аналогично на описания вече случай, ще се получи в резултат на необходимото позициониране на значещата част на цялото число, но вече спрямо новото положение на запетаята. Тя, както се вижда от рисунката по-горе, е позиционирана на (m-1) позиции вляво от десния край на разрядната мрежа. Като имаме предвид отношението (3.7.3) следва, че значещата част на цялото число може да е необходимо да се измества наляво (когато числото е по-късо от (m-1) бита) или надясно (когато е по-дълго от (m-1) бита). Така възникват 2 въпроса – в каква посока да се измества значещата част на цялото число и на колко бита?. Целта на това изместване е старшата единица на числото да попадне в бит №(-1), при което значещата част ще се приема за нормализирана мантиса. Казаното можем да илюстрираме със следната рисунка

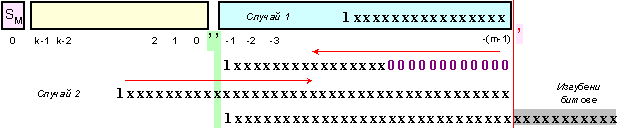
В първия случай, когато цялото число е по-късо от (m-1) бита, то се измества наляво до постигане на лявата нормалност. При това вдясно се добавят цифри нула. Броят на изместванията ще означим отново с h, при което порядакът на цялото число може да се определи така

В един брояч с начална стойност (m-1) след всяко изместване наляво ще се изважда единица, така в крайна сметка в брояча ще остане p_x. За получаване на характеристиката е необходимо да се добави отместването D. Нормализацията на мантисата във варианта, когато тя има скрит бит, не се отличава принципно в действията, описвани тук, ето защо си спестяваме тяхното изложение. Ще споменем само, че характеристиката се получава от порядък чрез добавяне на (D-1).

Във втория случай, когато дължината на цялото число е по-голяма от тази на полето, отредено за мантисата (m-1) бита, значещата част се измества надясно до постигане на лявата нормалност. В този случай порядакът на цялото число се определя така

което определя брояча като реверсивен. Както се вижда и от рисунката в този случай номализацията е свързана със загуба на младши цифри от значещата част на числото. Грешката, която при това настъпва, коментирахме по-горе.

За получаване на характеристиката е необходимо към получения порядък да се добави отместването D или (D-1). Към този случай може да се отнесе и числото X_min.

В крайна сметка в разрядната мрежа се сглобява изображението на числото от знак, характеристика и нормализирана мантиса. Последната е възможно да е неточна, ако е загубила част от младшите си цифри, което вече коментирахме по-горе.

В заключение твърдим, че всяко число, представено във форма с фиксирана запетая, може да се преобразува в число, представено във форма с плаваща запетая. При това не винаги точно. Грешката, свързана с по-малката дължина на полето за представяне на мантисата, се избягва в съвременните устройства за работа с ПЗ, тъй като те използват така наречения “вътрешен формат”, който има 64-битов формат за значещата част на числото. Все пак грешката се появява отново, ако потребителят поиска крайният формат за представяне на числото да бъде с по-малка дължина.

Б) Преобразуване на двоични числа с плаваща запетая в двоични с фиксирана запетая

Изходното число, представено във форма с плаваща запетая, в общия случай се превръща в число, чийто естествения вид има както цяла, така и дробна част (вижте фигура 1.1.6.1.2). Във форма с фиксирана запетая такова число не може да бъде изобразено, без да загуби дробната си част, т.е. това преобразование в общия случай не е точно. Обикновено то се реализира без закръгляне и представлява отделяне и представяне само на цялата част на числото. Например, числото 4,5 ще се представи като 4. В случаите, когато за формата с фиксирана запетая се използува същата дължина на разрядната мрежа, съществуват числа, които са непредставими и предизвикват препълване. Това се дължи на факта, че диапазонът на представимите числа за формата с плаваща запетая е много по-голям от този на формата с фиксирана запетая.

Всички числа с ПЗ, които имат отрицателен порядък, са числа по-малки от единица. В естествен вид, т.е. във форма с ФЗ, те имат нулева цяла част, ето защо в тези случаи преобразуването се свежда до просто нулиране на разрядната мрежа. Във всички останали случаи порядъкът на изходното число е положително число.

Същността на преобразуването е такова изместване на значещата част, т.е. на мантисата, при което тя ще има нулев порядък, тъй както например

Тук, при извеждане на математическите зависимости, имаме предвид структурата на разрядната мрежа с плаваща запетая от фигура 1.1.6.2.3, приведена тук за удобство.

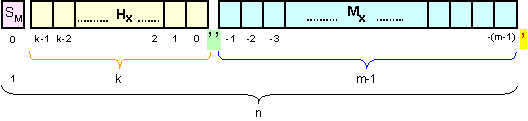
Мантисата е число с ляво фиксирана запетая, а цялото число – с дясно фиксирана запетая. Мантисата, която има (m-1) на брой цифри, следва да се измести така, щото броено от най-дясната позиция на разрядната мрежа, в нея да останат p_x на брой цифри. Тук следва да припомним на читателя, че порядъкът на числото показва колко са цифрите в цялата му част. Остава само да бъде определен броят на изместванията на мантисата. В случая следва да се реши уравнение (3.7.2) спрямо неизвестното h

За да използваме порядъкът p_x в годното уравнение, той трябва да бъде възстановен от характеристиката H_x.

В случай, че разрядната мрежа с плаваща запетая използува структурата от фигура 1.1.6.2.2, изместванията трябва да компенсират и k-битовата дължината на полето за порядък.

Тогава

Стойността h може да се изчисли, като от константата [(n-2)+1] (или респективно от константата [(n-2)+1+k] ) се извади стойността на порядъка p_x на изходното число. Ако получената разлика е положително число (h>0), посоката за изместване на мантисата е надясно, ако обаче е отрицателно (h<0) - посоката е наляво. Броят на изместванията е │h│, стойност, която се явява начална за изваждащ брояч, организиращ циклическия алгоритъм на последователно изместване. Последователното изместване на мантисата на повече от един бит е бавен процес, ето защо тук има място за приложение на рагледаното в раздел §3.5 програмируемо логическо изместване. Числото h се използва за инициализация на изместващата матрица.

Препълването, което е възможно да настъпи в разрядната мрежа с ФЗ, се открива чрез отношението

Горното отношение означава, че числото е по-дълго от разрядната мрежа. Ако порядъкът е равен на n и знака на числото е отрицателен, това е случай, когато числото е X_min, което е прдставимо в допълнителен код. Броят на числата, чиято дължина е по-голяма от (n-1) е огромен. Това се дължи на значително по-големия диапазон на представимите с ПЗ числа. Най-често отношението (3.7.8) е твърде силно (p_x>>>n) и води до препълване.

В края на това преобразование цялото число следва да се представи в разрядната мрежа в допълнителен код.

В заключение твърдим, че не всяко число, представено във форма с плаваща запетая, може да се преобразува в число, представено във форма с фиксирана запетая. Представимите с фиксирана запетая числа след преобразуване са значително по-малко. При загуба на дробната част цялата част, която остава, е точна. Както читателят може да забележи, и тези преобразования са свързани с принципни и неотстраними грешки, което засилва разбирането ни, че програмистът носи голяма отговорност за правилните и възможно най-точните резултати.

Описаните по-горе преобразования са илюстрирани с числени примери, които читателят ще намери в книга [2].

2. Преобразуване на формáта на числата

За по-голяма гъвкавост, универсалност и удобство, съвременните процесори поддържат различни формати на данните, но само такива, които са възможни в пълната апаратна дължина на разрядната мрежа. Това се изисква от езиците за програмиране. Формати, по-големи от този на разрядната мрежа, се моделират програмно.

Декларирането на променливите в една програма определя освен формата за представяне (ФЗ) или (ПЗ) още и формата (дължината) на полето за представяне. Така, в един алгебрически израз могат да се комбинират променливи и константи различни не само по форма, но и по формат. По този начин възниква нов по своята същност проблем. Тъй като АЛУ обработват еднакви по форма и формат операнди, следва преди изпълнението на основната операция задължително да се постигне тази еднаквост. Що се отнася до форматите, заявени от програмиста, възможните преобразования се свеждат до удължаване или до скъсяване. Естествено, при уеднаквяване в рамките на алгебрически израз, доминантен е по-дългия формат. Така, преди основната операция, по-късия формат следва да се удължи до по-дългия. Обикновено най-късият формат, който процесорите поддържат, е с дължина 1 байт. Когато става дума за числа с дясно фиксирана запетая, същите са представени в допълнителен код. Правилата за удължаване на късия формат са две:

1. Към изходния формат, в ляво от него, се добавя още една порция със същата дължина, т.е. удължаването е двойно. Ако изходния формат е 1 байт, се получават 2 байта. Това преобразование се извършва от машиннинни команди, като например командата CBW (Convert Byte to Word). За формат 2 байта съществуват команди CWD, CWDE (Convert Word to Doubleword), които постигат 32 битова дължина на формата за операнда. За различните модели процесори са разработени и други машинни команди, разглеждането на които обаче е извън контекста на нашите обяснения тук;

2. Добавеното поле, удължаващо отляво изходния формат, се запълва автоматично с цифри, които са определни от правилото, което вече много пъти сме пояснявали, наричано “правило за знаково удължаване”. Според него, добавеното отляво поле, се запълва с цифри, имащи стойността на знаковата цифра. Знаковата цифра е най-старшата (най-лявата) цифра в изходния формат.

Обратното преобразование, при което изходният формат следва да се скъсява, не се залага като изпълнима операция и машинни команди за него няма. Това е разбираемо по следните причини:

· Ако форматът се скъси чрез отрязване на младшата половина, рискувате на загубите младшата значеща част на съдържащото се число, което е груба грешка;

· Ако се отреже старшата половина, съществува риск от загуба на старши значещи цифри на числото (една или повече), което е още по-голяма грешка. Такава не съществува само в случай, че значещата част на числото се побира само в младшата половина на изходния формат. Това обаче не може да бъде предварително известно, особено за междинни числени стойности.

Следва да добавим още, че преобразуване на изходния формат, може да се наложи и в рамките на оператор за присвояване. Скъсяване на формат по принцип е възможно, но то може да бъде постигнато само програмно, ако алгоритъма, който програмистът реализира, го изисква. Ако такова преобразование се поиска от оператор за присвояване, тази ситуация се сигнализира като грешка още на етап компилиране на програмата.

Сега ще разгледаме темата при условие, че изходният операнд е представен във форма с плаваща запетая според фигура 3.7.2. Тези преобразования са два вида:

· при зареждане на операнд във входен регистър на FPU;

· и обратно, при запомняне на резултат, получен в FPU, в паметта в съответния формат MemF, заявен от програмиста.

Запомнените в паметта стойности имат структурата MemF:(S,H,M). Тези формати бяха означени като SP (единична точност) и DP (двойна точност). След прочитане на операнд от паметта той следва да се зареди във входен регистър на устройството за работа с плаваща запетая, при което трябва да се преобразува до пълния вътрешен формат от 80 бита (1+15+64). Като се имат предвид дължините на изходния формат SP от 32 бита (1+8+23) или на DP от 64 бита (1+11+52), става ясно, че както характеристиката Н, така и мантисата М, трябва да бъдат представени в полета с по-голяма дължина, а към мантисата още трябва да се конкатенира старша единица, стойност на скрития бит. Постигането на вътрешния формат на мантисата е лесно. Тъй като тя е число с ляво фиксирана запетая, удължаването й е отдясно чрез добавяне на необходимия брой незначещи нули. Например, ако изходният вид на мантисата е:

,bbbb … bbb - комбинация с дължина 23 или 52 бита

за вътрешния формат получаваме:

1,bbbb … bbb000 ... 000 - комбинация с дължина 64 бита

Характеристиката Н е цяло число, т.е. число с дясно фиксирана запетая. Стойността на това число се определя от формулата

H = p+(D-1) = (p-1)+D . (3.7.9)

От своя страна стойността на отместването D е равна на теглото на старшия бит в полето на характеристиката, т.е. D=2⁷ или D=2¹⁰ или D=2¹⁴ за съответните формати. Ако стойността (p-1) е положително число, видът на характеристиката може да бъде:

100...00bb…bb, - комбинация с дължина 8 или 11 бита.

Ако модулът на порядъка е достатъчно голям, е възможно комбинацията да има следния вид:

1bbb…bbb…bb, - комбинация с дължина 8 или 11 бита.

За да стане тази комбинация характеристика във вътрешния формат от 15 бита, след старшата единица се вмъкват (добавят) липсващите незначещи цифри нула (0):

100...0000...00bb…bb, - комбинация с дължина 15 бита, или

100...00bbb…bbb…bb, - комбинация с дължина 15 бита.

Добавеното поле (Supplement) има известна дължина, която ще означим с буква S. Дължината на това поле може да се изчисли както следва

където от дължината на полето за характеристика L_ЕР на вътрешния формат (15 бита) се изважда дължината на същото поле в по-късите формати (8 или 11 бита). Така дължината S на добавеното поле може да бъде 7 или 4 бита съответно.

Ако стойността (p-1) е отрицателно число, видът на характеристиката е:

011...11bb…bb, - комбинация с дължина 8 или 11 бита.

Ако модулът на порядъка е достатъчно голям, е възможно комбинацията да има следния вид:

0bbb…bbb…bb, - комбинация с дължина 8 или 11 бита.

За да стане тази комбинация характеристика във вътрешния формат от 15 бита, след старшата нула се вмъкват липсващите незначещи цифри единица (1):

011...1111...11bb…bb, - комбинация с дължина 15 бита, или

011...11bbb...bbb…bb, - комбинация с дължина 15 бита.

Преобразования не се изпълняват, когато числото пристига в устройството с формат EF, който съвпада с вътрешния, т.е. 80 бита или 10 байта.

Вторият вид преобразования се изпълняват, когато изчисленият в FPU резултат трябва да се запомни в паметта, където ще се съхранява в заявения от програмиста MemF. Не се извършват преобразования ако резултатът се запомня във формата, в който е получен (10 байта). В останалите случаи се налага скъсяване. Аналогично на преобразованията, описани по-горе, и тук се налага да се изяснят действията, свързани с двата основни елемента на структурата – характеристика и мантиса.

Характеристиката е цяло число, записано в поле с дължина 15 бита. Пренасянето на това число в поле с дължина 8 или 11 бита изисква скъсяване на изображението отляво. Но ако значещата част на съдържащия се в изображението порядък е достатъчно дълга, то той няма да може да се изобрази в по-късия формат. Така възниква въпросът - как да се разпознава тази ситуация? Ще приемем първоначално, че характеристиката изобразява положителен порядък, което пък означава, че най-старшият й бит е единица. Ако вдясно от тази единица съществува група от поне S на брой нули (0), то комбинацията има следния вид:

100...00bbb…bbb…bb, - комбинация с дължина 15 бита.

Отнемането на тази група от S на брой нули ще даде характеристиката в желания формат и тя ще има вида:

1bbb…bbb…bb, - комбинация с дължина 8 или 11 бита.

Ако обаче вдясно от старшата единица на характеристиката не съществуват S на брой последователни нули, това означава, че изобразеният порядък е по-голям от максимално възможния за потребителския формат на характеристиката. Това за преобразованието означава препълване на разрядната мрежа с искания по-къс формат.

Ако най-старшата цифра на характеристиката е нула, това означава, че изобразеният порядък е отрицателно число. Ако вдясно от тази нула съществува група от поне S на брой единици (1), то комбинацията има следния вид:

011...11bbb...bbb…bb, - комбинация с дължина 15 бита.

Отнемането на тази група от S на брой единици ще даде характеристиката в желания формат и тя ще има вида:

0bbb...bbb…bb, - комбинация с дължина 8 или 11 бита.

Ако обаче вдясно от старшата нула на характеристиката не съществуват S на брой последователни единици, това означава, че модулът изобразения порядък е по-голям от максимално възможния за потребителския формат на характеристиката. Това за преобразованието означава силно отрицателно препълване на разрядната мрежа с искания по-къс формат. Нормално е в този случай резултатът в по-късия формат на се замести с машинната нула.

И на края остана да изясним как се скъсява мантисата, което след всичко казано до тук, не е така неясно. Мантисата губи старшата си единица (скрития бит) и бива отрязана отдясно със съответния брой битове, така че от 63 да останат 23 или 52. С цел по-малка грешка е възможно да се изпълни закръгляне до младшия бит на формата MemF, в който се съхранява числото.

Илюстрация на изложените преобразования с числени примери читателят може да намери в книга [2].

Следващият раздел е:

§ 3.8 Обща организация на изпълнимите операции ( Common organization of executable operations )