Последната актуализация на този раздел е от 2020 година.

5.3.6 Откриване и премахване на зависимости между машинните команди при компилиране. Разгъване на цикли.

Вече многократно говорихме за задачите на компилаторите. Тук ще се спрем по-конкретно върху възможностите им да увеличават степента на паралелизъм, който може да се реализира по време на изпълнение на програмата. Ето защо следва да започнем със задачата за откриване на зависимостите и с отстраняването на зависимостите по имена (идентификатори).

А) Откриване и премахване на зависимости

Откриването на зависимостите по данни в една програма представлява важна част от три задачи:

1. Добро планиране на програмния код ;

2. Определяне на циклите, в които се съдържат паралелизми ;

3. Отстраняване на зависимостите по имена.

Сложността на анализа на зависимостите е свързана с наличието на масиви (и на указатели, в програми, написани на езици, подобни на Си). Тъй като обръщението към скаларните променливи се извършва явно, чрез техните имена, обикновено тези променливи се анализират достатъчно просто. Наличието в програмата на указатели и обръщението към параметри предизвиква усложнения, тъй като в процеса на анализ техните стойности могат да бъдат неизвестни. Анализът цели да се открият всички зависимости и да се определи съществува ли цикъл в тези зависимости, тъй като това е онова, което няма да ни позволи паралелно изпълнение на цикъла. Ще разгледаме следния пример:

for (i=1; i<=100; i=i+1) {

A[i] = B[i] + C[i] ;

D[i] = A[i] + E[i] ;

}

тъй като в дадения случай зависимостта, свързана с масива А, не води до зависимости между отделните итерации на цикъла, същият може да бъде разгънат за изявяване на паралелизма в по-висока степен. Не можем направо да разменим местата на двете обръщения към променливата А. Ако цикълът има зависимости между итерации, които не са циклически, може първоначално да го преобразуваме с цел отстраняване на тези зависимости, а после да го разгъваме, за изявяване на паралелизъм в по-висока степен. В много паралелни цикли степента на паралелизъм е ограничена само от броя на повторенията на тялото на цикъла, който пък от своя страна е ограничен само от броя на итерациите на цикъла. Разбира се на практика, за да спечелим от по-голямата степен на паралелизъм, се изискват много функционални устройства и голям брой регистри. Липсата на зависимости между итерациите на цикъла говори, преследваната голяма степен на паралелизъм е достъпна.

Приведеният по-горе алгоритмичен текст илюстрира също така и друга възможност за подобряване на машинния код. Второто обръщение към А не е необходимо да се компилира в команда за зареждане, тъй като ние вече знаем стойността, изчислена и записана от предидущия оператор. Ето защо второто обръщение към А може да се изпълнява като прочитане на регистър, съдържащ стойността. Изпълнението на тази оптимизация на кода изисква да се знае, че двете обръщения се отнасят до един и същи адрес от паметта, и че към тази същата клетка, между тези две обръщения, други обръщения с цел запис, няма. Обикновено анализът на зависимостите по данни дава разбиране само за това, че едното обръщение може да зависи от другото. За да се определи, че две обръщения следва да се извършват точно по един и същи адрес, е необходим по-сложен анализ. За по-горе приведения пример е достатъчна най-проста версия на такъв анализ, тъй като и двете обръщения се намират в един и същи базов блок.

Често зависимостите между итерациите на цикъла се появяват във формата на рекурентно отношение:

for (i=2; i<=100; i=i+1) {

Y[i] = Y[i-1] + Y[i] ;

}

Откриването на рекурентните отношения може да се окаже важно по две причини. Някои архитектури (особено векторните процесори) имат специална поддръжка за изпълнение на рекурентни отношения и някои рекурентни отношения могат да бъдат източник на паралелизъм с висока степен. Ще разгледаме например следния цикъл:

for (i=6; i<=100; i=i+1) {

Y[i] = Y[i-5] + Y[i] ;

}

По време на итерация №j цикълът се обръща към елемент №(j+5). Казваме, че този цикъл има зависимост с разстояние 5. Цикълът от предидущия пример обаче има зависимост с разстояние 1. Колкото по-голямо е разстоянието, толкова по-голяма е степента на потенциалния паралелизъм, който може да се получи чрез разгъване на цикъла. Например, ако ние разгънем първия цикъл, имащ зависимост с разстояние 1, последователните оператори зависят един от друг, има някаква степен на паралелизъм между отделните команди, но тя не е голяма. Ако разгънем цикъл, който има зависимост с разстояние 5, то има последователност от 5 команди, между които няма зависимости, като по този начин те притежават значително по-голяма степен на паралелизъм на ниво команди. Въпреки, че много цикли със зависимости между итерациите имат разстояние 1, случаите с по-големи разстояния на практика възникват и зависимостите с по-големите разстояния могат да осигурят достатъчна степен на паралелизъм, за да поддържат процесора зает.

Почти всички алгоритми за анализ на зависимостите, които се реализират в компилаторите, работят, изхождайки от предположението, че обръщенията към масивите са афинни. В най-простия случай индексът на елементите на едномерен масив е афинен, ако може да бъде записан във формата (a.i+b), където a,b са константи, а i – променлива на индекса на цикъла. Индексът на многомерен масив е афинен, ако всяка индексираща променлива в списъка на индекса е афинна. По този начин, откриването на зависимости между две обръщения към един и същи масив в цикъла се свежда до проверката, дали две афинни функции могат да имат една и съща стойност за различни индекси, между границите на цикъла. Например, ако предположим, че сме изпълнили запис в елемент от масив, чийто индекс има стойността (a.i+b), и изпълняваме зареждане в регистър от същия масив на друг елемент с индекс (c.i+d), където променливата i е индекс на цикъл for, който има интервала [m,n], тогава зависимост има, ако се изпълняват двете условия:

1. Ако има два индекса на две итерации – j и k, и двата в границите на цикъла for, които имат формата m.j и k.n ;

2. Ако се изпълнява запис в паметта на елемент от масива, индексиран с формата (a.j+b) и след това се изпълнява зареждане на елемент от същия масив, индексиран с формата (c.k+d), при което (a.j+b)= (c.k+d).

В общия случай по време на компилация не може да се определи има ли зависимости. Например, стойностите на променливите a, b, c, d могат да бъдат неизвестни, могат да бъдат елементи на друг масив и следователно е невъзможно да се каже, че зависимост съществува. В други случаи проверката за зависимости може да се окаже доста скъпа, но по принцип възможна по време на компилация. Например, обръщенията могат да зависят от индексите на итерациите на множество вложени цикли. Много програми обаче съдържат главно прости индекси, в чиито форми променливите a, b, c, d са константи. В такива случаи, за откриване на зависимостите, могат да се съставят не особено скъпи тестове. Така например прост и достатъчен тест за отсъствие на зависимости е най-големият общ делител (текст НОД). Той се базира на разбирането, че ако съществува зависимост между итерациите на цикъла, то НОД(c,a) трябва да дели разликата (d-b). Тук се има предвид целочислено деление без остатък. НОД-тестът е достатъчен, за да се гарантира, че зависимости няма. Съществуват обаче случаи, когато НОД-тестът постига целта си, но в реалната програма да има зависимост. Такава ситуация е възможна, ако НОД-тестът пропуска разглеждането на границите на цикъла.

В общия случай задачата за определяне на действителното съществуване на зависимостите изисква пълна проверка на всички възможни случаи (задачата е NP-пълна). На практика обаче много частни случаи могат да бъдат анализирани с помощта на сравнително евтини тестове. Тестът е точен ако той определя точно съществуването на зависимостите.

Освен че се опитва да определи има ли зависимости, компилаторът се старае и да ги класифицира по тип. Това му позволява да отделя зависимостите по имена и да ги отстранява чрез техниката на преименуване и копиране. Следващият цикъл например, съдържа няколко типа зависимости. Ще се опитаме да намерим всички истинни зависимости, зависимостите по изход и анти-зависимостите и да ги отстраним чрез преименуване.

for (i=1; i<=100; i=i+1) {

Y[i] = X[i] / c ; /*S1*/

X[i] = X[i] + c ; /*S2*/

Z[i] = Y[i] + c ; /*S3*/

Y[i] = c - Y[i] ; /*S4*/

}

В тези четири оператора съществуват следните зависимости:

1. Има истинни зависимости от S1 към S3 и от S1 към S4 заради Y[i]. Отсъстват зависимости между итерациите на цикъла, което позволява да разглеждаме цикъла като паралелен. Тези зависимости водят до това, че операторите S3 и S4 ще изчакват изпълнението на оператор S1 ;

2. Има анти-зависимост от S1 към S2 ;

3. Има зависимост по изход от S1 към S4.

Следващият текст не съдържа изявените зависимости:

for (i=1; i<=100; i=i+1) {

/* Y се преименува на T за да се отстрани

зависимостта по изход */

T[i] = X[i] / c ;

/* X се преименува на X1 за да се отстрани

анти-зависимостта */

X1[i] = X[i] + c ;

Z[i] = T[i] + c ;

Y[i] = c - T[i] ;

}

След цикъла променливата Х се оказва преименувана в Х1. В кода на програмата, след цикъла, компилаторът може отново да възстанови името Х1 на Х. В дадения случай преименуването не изисква действително копиране и може да бъде изпълнено като смяна на името или чрез съответното разпределение на регистрите. В други случаи обаче преименуването може да изисква копиране.

Анализът на зависимостите представлява най-важната технология за подобряване използването на паралелизма. На ниво команди тя дава информация, необходима за измененията в процеса на планиране реда на обръщенията към оперативната памет, а така също и за полезността от разгъването на циклите. За откриване на паралелизма на ниво цикъл анализът на зависимостите представлява базов инструмент. Ефективната компилация на програмите за векторните процесори, а така също и за многоядрените процесори, съществено зависи от този анализ. Освен това, при планиране на потока команди е полезно да се определи, са ли потенциално зависими обръщенията към паметта. Основният недостатък на анализа на зависимостите се състои в това, че той е приложим при ограничен набор обстоятелства, а именно за обръщенията вътре в един цикъл и използва афинни функции на индексите. Така остава огромно многообразие от ситуации, при които анализът на зависимостите не може да съобщи за онова, от което ние се интересуваме, а именно:

· Кога обръщенията към обектите се изпълняват чрез указатели, а не чрез индексите на масивите ;

· Кога индексацията на масивите се осъществява косвено, чрез друг масив, която индексация се прилага при работа с разредени масиви (разредени матрици) ;

· Кога съществува зависимост за някои стойности на входовете, но липсват в действителност при изпълнението на програмите, тъй като входовете никога не приемат определени стойности ;

· Кога оптимизацията зависи не просто от познаването на възможностите за съществуване на зависимости, но изисква точното определяне на това, от коя операция запис зависи четенето на променливата.

Б) Програмна конвейеризация: символично разгъване на цикли

Вече показахме, че един от методите за компилиране (разгъване на цикли) е полезен в това, че увеличава степента на паралелизъм на ниво команди, чрез създаване на по-дълги линейни структури. Съществуват още два важни метода, които са разработени за същата цел: програмна конвейеризация и планиране на трасетата.

Програмната конвейеризация е метод за реорганизация на циклите по такъв начин, че всяка итерация в получения код се състои от команди, които са избрани от различни итерации на първоначалния цикъл. В процеса на планиране по същество се подреждат команди от различни итерации на даден цикъл така, че да се отдалечат една от друга зависимите команди, възникващи в рамките на една итерация. Програмно конвейеризираният цикъл редува команди от различни итерации без реално разгъване на цикъла. Този процес е илюстриран на фигура 5.3.6.1.

По същество методът изпълнява програмно онова, което прави алгоритъмът на Томасуло, но с помощта на апаратни средства. Програмно конвейеризираният цикъл ще съдържа по една команда, отнасяща се към различни итерации на цикъла. При начално влизане в цикъла (при пролог) и при излизане от цикъла (при епилог) се изискват някои допълнителни команди.

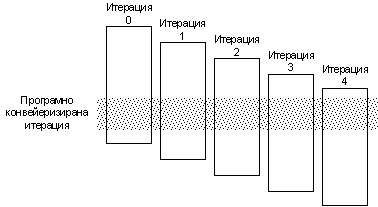
Фиг. 5.3.6.1. Процес на програмна конвейеризация

Ще разгледаме програмно конвейеризираният вариант на цикъл, който събира всеки елемент от даден масив, чийто начален адрес е записан в регистър R1, със съдържанието на регистър F2.

Loop: LOADD F0, 0(R1)

ADDD F4, F0, F2

STORED 0(R1), F4

SUBI R1, R1, #8

BNEZ R1, Loop

Следващата схема показва тялото на цикъла в три последователни итерации, разположени във времето през един такт, така както биха били зареждани командите в конвейера. В резултат на това представяне се вижда как се образува множеството от команди, изпълнявани в различни итерации и възможността за тяхното програмно конвейеризирано планиране.

Фиг. 5.3.6.2. Възможност за програмна конвейеризация

След горната илюстрация, игнорирайки пролога и епилога на цикъла, можем да препишем цикъла по следния начин:

Loop: STORED 0(R1), F4 ; // записва съдържанието на F4 в M[i]

ADDD F4, F0, F2 ; // събира съдържанието на F2 с M[i-1]

LOADD F0, -16(R1); // зарежда в регистър F0 елемент M[i-2]

BNEZ R1, Loop

SUBI R1, R1, #8 ; // формира нова стойност на адреса

Ако не се вземат под внимание пролога и епилога, този цикъл може да работи със скорост от 5 такта за една итерация. Тъй като командата LOAD извлича операндите със стъпка 2 елемента, цикълът следва да има 2 итерации по-малко. При това, преди началото на цикъла, съдържанието на регистър R1 следва да се намали с 16. Ще отбележим, че повторното използване на регистрите (например F4, F0 и R1), изисква използването на специални апаратни средства, за да се заобиколят конфликтите от тип WAR и задръжките в конвейера. В дадения пример такива не са необходими, тъй като никакви задръжки поради зависимости по данни не са наложителни.

Управлението на регистрите в програмно конвейеризираните цикли може да бъде достатъчно сложно. Последният пример не е достатъчно сложен за илюстрация на тези проблеми, тъй като в регистрите се изпълнява запис в една итерация, а тяхното четене става в следващата итерация. В други случаи може да се изисква увеличение на броя на итерациите между момента на зареждане на командата и момента, когато нейният резултат се използва. Това се случва, когато в тялото на цикъла се съдържа неголям брой команди, а задръжките при тяхното изпълнение са достатъчно големи. В такива случаи се налага използването на комбинация от методите за програмна конвейеризация и разгъване на цикли.

Програмната конвейеризация може да бъде разглеждана и като символично разгъване на цикъл. В действителност, някои алгоритми за програмна конвейеризация използват разгъването на цикъл в качеството на изходен материал за изготвяне на последващата програмна конвейеризация. Главното достойнство на програмната конвейеризация по отношение на прякото разгъване на цикъла се състои в това, че тя генерира по-малък по обем програмен (машинен) код. Програмната конвейеризация и в допълнение разгъването на цикъла позволяват по-добро планиране на вътрешния цикъл и от само себе си съкращават различни по тип излишни разходи. Така например, разгъването на цикъла съкращава разходите за организацията му, свързани с командите за преход и с модификацията на индекса (брояча) на цикъла. Програмната конвейеризация от своя страна съкращава времето, в което цикълът не работи с пълната си скорост, което се случва само по един път в началото и в края на цикъла. Ако разгъваме четирикратно цикъл, който изпълнява 100 итерации, то ще направим излишни (допълнителни) разходи 25 пъти (100/4=25 – всеки път, когато се инициира разгънатия цикъл). На следващата фигура 5.3.6.3 това поведение е изобразено графично.

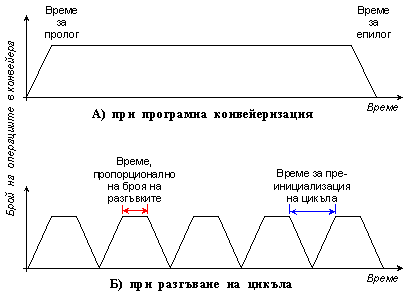
Фиг. 5.3.6.3. Времедиаграми на изпълнението на програмата

Тъй като тези два метода са насочени срещу различни по характер разходи, най-добре е те да се прилагат съвместно.

Друг метод, който се използва за изявяване на допълнителен паралелизъм представлява трасиращото планиране. Трасиращото планиране разширява метода за разгъване на цикли чрез методика за откриване на паралелизми в разклонени програмни структури, които не са свързани с циклически такива. Освен това трасиращото планиране е полезно за процесори с голям брой машинни команди, подавани за изпълнение в един такт, където само разгъването на циклите може да се окаже недостатъчно за изявяване на необходимата степен на паралелизъм за командното ниво, необходим за поддържане в заето състояние на конвейера. Трасиращото планиране представлява комбинация от два отделни процеса.

Първият процес, при който се избира трасето, се старае да намери възможна последователност от базови блокове, чиито операции могат да се поберат в по-малък брой команди. Разгъването на цикли се използва за генериране на дълги трасета, тъй като преходите при затваряне на цикли са изпълними с висока вероятност. Допълнително при използване на статично прогнозиране на условните преходи, останалите, не свързани с организацията на цикъла условни преходи, също избират своето направление и по този начин се получава една верига от последователно конкатенирани базови блокове. Тази верига представлява избраното трасе.

Върху избраното трасе работи вторият процес, чиято задача е да го уплътни, ето защо той носи това име (trace compaction). Уплътняващият процес се старае, чрез пренасяне на операциите колкото се може по-близо до началото на трасето, да го свие (компресира) в минимален брой дълги команди или пакети за зареждане в конвейера. Уплътнението на трасето представлява процес на глобално планиране на кода. Има две ограничения, които възникват и трябва да се обработват от всяка схема за глобална оптимизация на кода:

· Зависимости по данни, които изискват определен ред за изпълнение на операциите ;

· И точките на условните преходи, които създават (образуват) такива места, през които командите не могат да бъдат премествани.

Машинният код трябва да бъде уплътнен в най-къса последователност, която да съхрани зависимостите по данни и по управление. Зависимостите по данни се преодоляват чрез разгъване на циклите и чрез анализ на зависимостите за определяне на това, дали две обръщения към паметта се планират по един и същи адрес. Зависимостите по управление се съкращават още и при разгъване на циклите. Достойнството на методиката на трасиращото планиране, в сравнение с по-простите методи за планиране зареждането на конвейера, се състои в това, че тя осигурява схема за намаляване на ефекта от зависимостите по управление, чрез пренос на команди през условните преходи, които не са свързани с организацията на циклите, използвайки прогнозираното поведение на преходите.

По-долу на фигура 5.3.6.4 е показана блок-схемата на условен оператор, която можем да разглеждаме като една итерация на разгънат цикъл и избраното трасе.

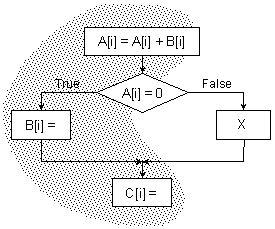
Фиг. 5.3.6.4. Фрагмент с разклонение и избраното трасе

Когато трасето, както е показано по-горе на блок-схемата, е избрано, то трябва да бъде употребено така, че да бъдат запълнени машинните ресурси. Уплътняването на трасето е свързано с преместване на операциите присвояване (машинните команди за запис) на променливите В и С нагоре по структурата на блока така, че да застанат преди точката, в която се определя посоката на прехода. Всяка схема за глобално планиране, включително и тази на трасиращото планиране, изпълнява такова преместване на команди, в условията на множество ограничения. В трасиращото планиране условните преходи се разглеждат като безусловни преходи във вътрешността на избраното трасе или извън него (което зависи от съответната прогноза), тъй като трасето, според определението му, представлява най-вероятния път, по който преминава реалното изпълнение на програмата. Когато командите се пренасят през такива входни или изходни точки на трасето, във входните и във изходните точки понякога се налага добавянето на допълнителни команди. Основното предположение при това се състои в това, че избраното трасе е най-вероятното събитие. В противен случай допълнително извършваната работа (от допълнителните команди) може да се окаже значителна по обем.

Какво по същество представлява процесът на пренасяне на операциите присвояване на променливите В и С? Изчислението на стойността и присвояването й на В е зависимо по управление от условния преход, докато в същото време изчислението на С не е зависимо. Преместването на тези оператори може да бъде изпълнено само, ако нито един от тях не променя зависимостта по управление и по данни, или ако ефектът от измененията на зависимостта не е виден и по този начин не се изменя изпълнението на програмата. Нека разгледаме типична последователност от команди, генерирана за ситуацията, илюстрирана на фигура 5.3.6.4. В текста се предполага, че адресите на променливите А, В и С, се намират в регистрите R1, R2 и R3 съответно.

LOADW R4, 0(R1) ; // зареждане на елемент A[i]

ADDI R4, R4, ... ; // събиране с A[i]

STOREW 0(R1), R4 ; // запис на елемента A[i]

... … … … …

BNEZ R4, elsepart ; // проверка на A[i]

... … … … … ; // тяло на клона then

STOREW 0(R2), ... ; // запис на елемента B[i]

JUMP join ; // прескачане на клона else

elsepart: ... … … … … ; // тяло на клона else

X ; // команден код за X

... … … … … ;

join: ... … … … … ; // обща точка след if

STOREW 0(R3), ... ; // запис на елемента C[i]

Най-напред ще разгледаме проблема с преместването на операция присвояване на В в положение преди командата за условен преход BNEZ. Тъй като променливата В зависи по управление от този преход, преди който искаме да я поставим, и след преместването вече няма да зависи от него, то е необходимо да се гарантира, че операцията не може да предизвика изключителна ситуация, тъй като такава изключителна ситуация не може да възникне в първоначалната програма, ако би бил избран клонът else на условния оператор. Преместването на присвояването на В не трябва също така да въздейства и на потока от данни. За да определим по-ясно изискванията, ни е необходима концепция (разбиране) за жизненост на променливата. Променливата Z живее в един оператор, ако съществува път за изпълнение от този оператор до друг оператор, който използва тази променлива, без да й присвоява нова стойност.

Разглеждайки нашия пример, могат да бъдат различени два възможни случая, в които преместването на В може да промени потока данни в програмата:

1. Към променливата В се извършва обръщение в кода на блок Х (в кода на клон else) в момент, преди на В да бъде присвоена нова стойност ;

2. Променливата В “живее” в края на оператора if и на нея не се присвоява нищо в блок Х.

И в двата случая преместването на операция присвояване на променливата В ще доведе до това, че някоя команда j (или в блок Х, или по-нататък в програмата) ще стане зависима по данни от така преместената команда, а не от по-ранна операция присвояване на В, която се изпълнява преди началото на цикъла и от която команда j първоначално е била зависима. Тъй като това ще доведе до промени в резултата на програмата, операция присвояване на В не може да бъде преместена в случая, ако е справедливо което и да е от посочените по-горе две условия.

Можем да си представим и по-прецизни схеми: например, в първия случай преди оператора if може да се направи копие на В и в блок Х да се използва само това копие. Такива схеми в общия случай не се използват, тъй като, първо, те са трудни за реализация и второ, тъй като те ще забавят програмата, ако избраното трасе не е оптимално и ако завършването на операциите изисква допълнителни команди.

За преместване на операцията присвояване на С в място непосредствено след първия условен преход, се изисква тя да бъде преместена по-високо от точката, в която се обединява трасето (входът на трасето) с клона else. Това прави командите за променливата С зависими по управление от условния преход и означава, че те няма да се изпълняват, ако бъде избран клона else, който не влиза в трасето. Затова ще бъдат засегнати командите, които са били зависими по данни от присвояването на С, и които се изпълняват след този кодов фрагмент. За да се осигури изчисляването на коректна стойност, се прави копие на онези команди, които изчисляват и присвояват стойност на С при стъпване на трасето, а именно в края на блок Х в клона else. Можем да преместим присвояването на С от клона then през условния преход, ако това не въздейства на някой даннов поток. Ако С се премества преди условната проверка, копието на С в клона else може да бъде премахнато.

Всички разгледани методи: разгъване на цикъл, планиране на трасе и програмна конвейеризация, се стараят да увеличат степента на паралелизъм в нивото на командите, който може да се използва в процесори, зареждащи за изпълнение повече от една команда за един такт. Ефективността на всеки един от тези методи и тяхното удобство за различните архитектурни подходи представляват най-горещите теми, с които се занимават конструкторите на високо производителните процесори.

Следващият раздел е:

5.3.7 Апаратни средства, поддържащи висока степен на разпаралелване