Този
раздел е
новосъздаден
през 2021
година.
5.5.2 Метастабилност.
Асинхронни
арбитри.
Арбитриране
в условия на
суперскаларност
– Продължение
2
В
древногръцката
митология се
разказва за Сизиф
строител и
цар на град Коринт
(около 1400 пр.н.е.). Никой
в Гърция не
можел да се
равнява по
коварство,
хитрост и
ловкост на
ума на Сизиф.
Благодарение
на своята
хитрост той
натрупал
несметни
богатства в
Коринт.

град
КОРИНТ
(древен
ЕРИФ)
Надалеч
се разнесла
славата на
неговите съкровища.
Сизиф
забелязал, че
Зевс
похищава
тайно
нимфата Егина
и го издал на
баща ѝ –
речния бог Азип.
Това
разгневило
Зевс и той
заповядал на бога
на смъртта,
мрачният Танатос,
да го заведе
долу, в
печалното
царство на Хадес.
Сизиф
почувствал
приближаването
на бога на
смъртта
Танатос,
затова
коварно го
подвел и
оковал във
вериги.
Тогава
хората на
Земята
престанали
да умират.
Никъде не
ставали вече
великолепни
погребения,
хората
престанали и
да принасят
жертви на
боговете от
подземното
царство. Бил нарушен
редът,
установен от Зевс
на Земята. И
ядосаният
гръмовержец Зевс
изпратил при Сизиф
могъщия бог
на войната Арес.
Арес освободил
Танатос от
оковите, а Танатос
изтръгнал
душата на Сизиф
и я отнесъл в
царството на
сенките на
умрелите.
Разказват
още, че пред
прага на
смъртта Сизиф
неблагоразумно
пожелал да
провери
любовта на
съпругата си Меропа
като й
поръчал да не
погребва тялото
му, а да го
остави на
градския
площад и да
не принася
жертви на
подземните
богове. Жена
му го
послушала. Разгневен
от подобна
покорност,
толкова противоположна
на човешката
любов, Сизиф издействувал
от Плутон
разрешение
да се върне
на Земята, за
да накаже
жена си и да й
заповяда да
принесе
богати
жертви, като
обещал след
това да се
върне обратно
в царството
на сенките
(царството на
Хадес).
Разбира
се, Сизиф не
се върнал в
Хадесовото
царство и не
бързал да
накаже жена
си. Когато
отново видял
света, когато
пак се
насладил на
водата и
слънцето, на
затоплените
камъни и на
морето, той
отказал да се
върне в
пъкления
мрак. Останал
в разкошния
си дворец и
весело пирувал,
като се
радвал, че
единствен
измежду всички
смъртни е
съумял да се
върне от
мрачното
царство на
сенките.
Подканите,
гневът и
предупрежденията,
които му
изпращали
боговете, не
послужили за
нищо. Той
живял още
много години
в залива, край
блесналото
море, сред
земните
наслади. Това
не можело да
се търпи, Хадес
се разгневил
и пак
изпратил Танатос
да вземе
душата на Сизиф.
Танатос се
явил в
двореца на
най-хитрия от
смъртните и
го заварил на
великолепен
пир. Омразният
и на
боговете, и
на хората бог
на смъртта измъкнал
душата на Сизиф
и я отнесъл
завинаги в
царството на
сенките.
В
задгробния
живот Сизиф
изтърпява
тежко
наказание
заради
всичкото си
коварство,
всичките
измами, които
е извършил на
Земята. Той е
осъден да
изкачва на
една висока,
стръмна
планина
грамаден камък.
Напрягайки
всички сили, Сизиф
работи
денонощно!
Едри капки
пот се стичат
от него
поради
тежката
работа. Все
по-близо е
върхът; още
малко усилие
и край на
Сизифовия
труд! Но
камъкът се
изплъзва от
ръцете му и с
трясък се
търкулва
надолу, като
вдига облаци
прах. И Сизиф
отново се
залавя за
работа ....
Сизиф
(картина на
Тициан) Сизиф
(картина от
Франц фон
Щук)


Уважаеми Читателю, разказахме тази кратка история по две причини: първо, за да те развеселим и второ, защото тя е една своеобразна прелюдия към същността на явлението метастабилност, на чието изясняване е посветен този пункт.
Проблемите, за които ще говорим тук, започват от момента, когато започва изследването на логически схеми с обратни връзки. Алгебрата на логиката и синтезът на логическите схеми, като нейна техническа реализация, започва с комбинационните схеми. Те най-общо се характеризират с това, че всички входни сигнали, както и всички междинни такива, се разпространяват по логическите връзки в схемата в посока на изходните точки. Такива схеми е прието да наричаме комбинационни. Логическите стойности на изходните функции не зависят от времето, което ни дава право да ги наричаме вечни. Идва обаче моментът, в който следва да се изследват логически схеми с обратни връзки. Най-елементарните такива схеми са показаните по-долу.
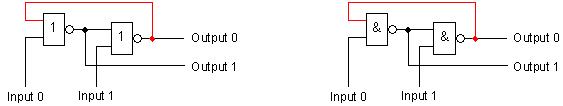
Фиг. 5.5.2.2.1. Елементарни логически схеми с обратна връзка
Известно е, че благодарение на обратната връзка горните логически схеми придобиват забележителното свойство паметливост и са добре известни под наименованието Latch RS-тригери. Това би следвало да е добре известно на читателя и ние няма да го доказваме тук.
Най-често представените две схеми се чертаят по следния начин:
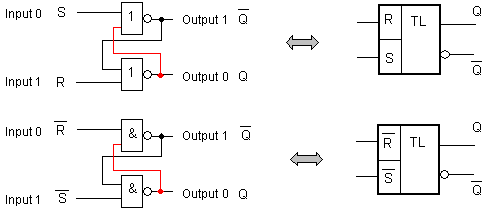
Фиг. 5.5.2.2.2. Логически схеми на елементарни асинхронни Latch RS-тригери и съответното им УГО (условно графично означение)
Схемите се определят като елементарни тригери или като градивни елементи с памет, които могат да съхраняват дълго време една логическа стойност (0 или 1). Първата схема, изградена от два елемента ИЛИ-НЕ (NOR) представлява асинхронен Latch тригер с право управление, т.е. неговото състояние, което се представя от изхода Q, се повлиява от входната логическа стойност “1" (Input=1). При това входната комбинация от две едновременни единици (Input 0 = 1, Input 1 = 1) се счита за забранена. При съответно показаното означение на изходите Q и notQ, входовете се определят като R и S според тяхното въздействие на схемата. При S=1, R=0, схемата се установява в състояние Q=1 (notQ=0), и обратно – при S=0, R=1, схемата се установява в състояние Q=0 (notQ=1).
Аналогичното може да се каже за втората схема, изградена от два елемента И-НЕ (NAND). Нейното състояние, което се представя от изхода Q, се повлиява от входната логическа стойност “0" (Input=0). При това входната комбинация от две едновременни нули (Input 0 = 0, Input 1 = 0) се счита за забранена. Схемата се определя като асинхронен Latch тригер с инверсно управление, което се изразява в условното графично означение (УГО) чрез инверсиите на входовете: notR и notS.
Когато се смени входната комбинация, се променя изходното състояние на тригера – говорим че той се превключва. Говорим още, че тригерът приема (записва, фиксира) активната входна стойност, която се запазва като ново изходно състояние на тригера след изчезването й. Последното означава, че активната входна комбинация се сменя с неактивна такава (R=0, S=0 за тригери с право управление и R=1, S=1 за тригери с инверсно управление). Именно в това се изразява свойството паметливост, за което беше споменато по-горе.
Метастабилност
при
асинхронни
тригери
Нека сега да се спрем на процеса, наречен превключване. Ще разгледаме тригер с право управление. Нека да приемем, че тригерът се намира в състояние нула (Q=0). В даден момент t0 подаваме входна комбинация R=0,S=1. Според казаното по-горе тригерът следва да се превключи в състояние Q=1. На практика обаче превключването не се случва мигновено, за това е необходимо време. Времето е необходимо за разпространение на входното въздействие във вътрешността на електронната схема, в резултат на което тя ще изчисли новата стойност на изходното напрежение. Обикновено във времедиаграмите, представящи процеса на превключване, забавянето се изразява с наклонен фронт на сигнала.
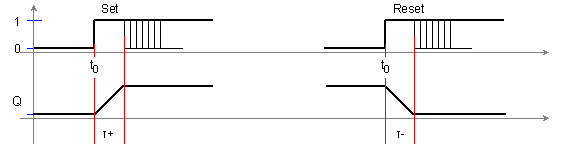
Фиг. 5.5.2.2.3. Времедиаграма на превключване
Както се вижда от рисунката, след команда Set, за установяване на състояние Q=1 е необходимо времето τ+ (преден или положителен фронт), а след команда Reset, за установяване на състояние Q=0 – необходимото време е τ- (заден или отрицателен фронт).
Всяко отнемане на входната команда преди изтичане на времето за превключване е опасно за стойността на крайното изходно състояние. Това е така, защото електронната схема, върху която се въздейства, съдържа обратни връзки, благодарение на които процесът на нейното превключване се определя като лавинообразен. Както се вижда от рисунката, командите могат да бъдат безопасно отнемани само след изтичане на посочените закъснения (τ+ или τ-). Крайното изходно състояние е гарантирано само ако продължителността на входното въздействие удовлетворява условието:
<Продължителност на команда Set> ≥ τ+ ; <Продължителност на команда Reset> ≥ τ- .
При отнемане на входната команда по-рано, т.е. когато тя е с недостатъчна продължителност, вътрешното състояние на схемата е нестабилно и се нарича метастабилно. Обикновено при неговото обяснение се използва следната илюстрация:
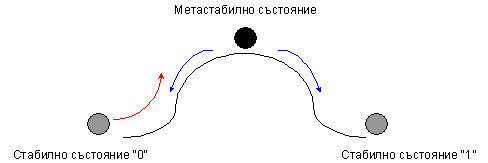
Фиг. 5.5.2.2.4. Илюстрация на явлението метастабилност
Метафорично, недостатъчната продължителност на командата за превключване е причина за неопределения край на процеса. Недоактивираните лавинообразни процеси в електронната схема не гарантират тяхното правилно развитие. В резултат крайното състояние на схемата е несигурно, негарантирано може да бъде 0 или 1. Многократните практически експерименти са илюстрирани със следната осцилограма.
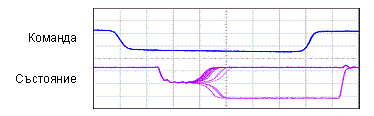
Фиг. 5.5.2.2.5. Осцилограма, илюстрираща явлението метастабилност
Вероятно читателят вече разбира аналогията на метастабилното превключване с историята за Сизиф, която разказахме в началото.
Метастабилност
при
синхронни
тригери
Основният метод за управление на тригерите и на логическите възли, изградени с тригери, е синхронният. Той разделя входните данни от командите за превключване. Обикновено практически говорим за запис на нови данни в тригер или регистър. Записът се извършва в момент на подаване на команда за това, която се интерпретира с появата на съответния синхроимпулс. Този начин на управление и свързаната с него терминология, както и начин на говорене е изложен подробно в книга [3] и ние настоятелно препоръчваме на читателя да се запознае със съответното изложение.
http://www.tyanev.com/home.php?lang=bg&mid=18&mod=1&b=8&s=417
Синхронното управление усложнява в известна степен анализа на явлението метастабилност, което води до необходимост от въвеждане на нови параметри. Най-лесен за анализ е синхронният Latch D-тригер.
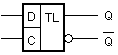
След горния указател ние считаме, че подробното представяне на този тип тригер не е необходимо и ще се спрем само върху процеса на неговото превключване. Към схемата на тригера са подведени поне две входни връзки – едната за данните, която е присъединена към вход D на тригера, другата за управляващия синхроимпулс, присъединена към вход C (Clock) на тригера.
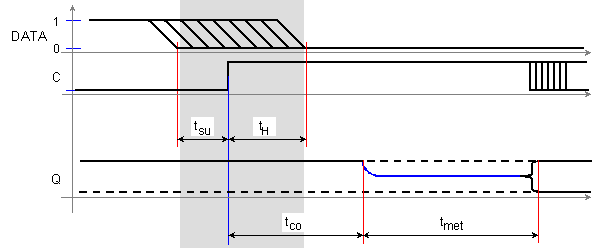
Фиг. 5.5.2.2.6. Параметри на синхронната метастабилност
tSU - register setup time (време за предварение за установяване на данните) ;
tH - register hold time (време за удържане на данните) ;
tCO - clock to output delay (време за достигане на метастабилната точка) ;
tmet - време на мъждене .
Рисунката показва, че всяка промяна в стойността на сигнала DATA в показания времеви интервал, води до не гарантирано превключване на състоянието Q, т.е. води до метастабилност.
При нарушение на времевите параметри понякога процесите излизат извън границите на “дигиталния свят”, който е своеобразна част от аналоговия. Излизайки от тези граници, изходната величина на тригера се колебае в междинно състояние, с напрежение, съответстващо на половината от стандартното, приемащо се за единица. В крайна сметка тригерът ще се превключи в едно от крайните си състояния, но да се каже в кой точно момент ще стане това, е невъзможно. Времевият престой на схемата в метастабилно състояние е вероятностна величина, която зависи от технологичните параметри на електронните елементи, от температурата, от флуктуациите на захранващото напрежение, от нивото и флуктуациите на входните сигнали и пр.
В крайна сметка трябва да кажем, че за надеждно и успешно превключване на тригера, Конструкторът следва да осигури изпълнението на следните условия:
1. Да подаде входните данни и да осигури тяхната стабилност с предварение не по-малко от tSU секунди до появата на активния фронт на управляващия синхросигнал ;
2. Да продължава да удържа и да не отнема входните данни най-малко tH секунди след появата на активния фронт на управляващия синхросигнал ;
3.
Да
реализира
достатъчна
продължителност
на активната
фаза на
управляващия
синхросигнал
(не по-малка
от tGO + tmet
секунди).
Когато подаването на входните данни нарушава минималните интервали tSU и tH изходът на тригерите в един регистър могат да преминат в метастабилно състояние. В метастабилно състояние изходът на тригерите зависват при стойност между високото и ниското ниво за определен период от време, което означава, че изходното превключване към истинното ниво се забавя над определеното време tCO .
Конкретните стойности на времевите параметри на елементната база Конструкторът следва да получи от фирмите производителки.
Ефектът метастабилност може да възникне в няколко класически ситуации:
1. При явно нарушение на посочените по-горе условия. Това са ситуации, когато се опитват да заставят устройството да работи на повишена тактова честота, на което пречи дължината на свързващите проводници ;
2. При явно нарушение на времевите параметри по входовете за асинхронен ресет. Въпреки че ресетът обикновено е асинхронен акт, той следва да бъде синхронизиран с тактовия сигнал на този тригер, който се ресетира ;
3. Синхронно подавани сигнали (на еднаква тактова честота, но с известно закъснение) от други устройства. В такива случаи се налага не прост анализ на времевите съотношения ;
4. И най-тежкият случай – сигналите се предават асинхронно и може би на съвсем друга тактова честота (и с неизвестни фазови отмествания) спрямо приемните тригери ;
5. При несъответствие на нивата на входните сигнали, определени чрез съответния стандарт, за логически стойности. Това е възможно и при несъответствие на нивото на захранващото напрежение или при негова нестабилност.
Арбитър.
Асинхронно
арбитриране
Думата арбитър е достатъчно позната. Обикновено тя се свързва с някой (или с нещо), който (което) има за задача да отсъди правото в полза на един от поне двама спорещи. В реалния човешки живот, който се регулира от общо известни морални норми и правила, при достигане на конфликтна ситуация и до спор, цивилизовано е последният да се отнесе за разрешаване до юридическо ведомство, институция на гражданското общество. Казано с други думи, спорът се решава от съд, който играе ролята на арбитър между спорещите страни. Често арбитърът е задължителен, особено в сферата на спорта.
В условията на компютърната техника, която е нашият обект на внимание, също настъпват ситуации, в които две или повече събития претендират за правото да владеят даден технически ресурс или правото да извършат определено действие върху съответен обект. Това право всяко от събитията се стреми да получи в резултат на състезание във времето. Убедени сме, че всичко това е достатъчно разбираемо за читателя, въпреки, че не е изказано конкретно. В този смисъл смятаме, че не е необходимо да се мотивираме повече и можем да заключим с извода, че проблемът на арбитрирането е реален за компютърната техника. Следва да разгледаме технически средства, които могат да играят ролята на арбитър.
Арбитриране
без
приоритет
Искаме
да
предупредим
читателя, че
тук не е
редно да
търси
аналогия с
проблема избор.
Този проблем
беше
разгледан
по-рано тук в § 5.4,
където бяха
представени
различни
схеми за
избор на
заявка за
прекъсване
според нейния
приоритет.
Тук
читателят
следва задълбочено
да вникне в
същността на
постановката
за арбитриране,
в противен
случай той ще
бъде объркан,
което ние
наблюдаваме
в
публикациите
на много
автори,
приемащи се
за
компетентни
или не толкова.
Съвременните разработки в областта на компютърните технологии се характеризират с неистови усилия за постигане на все по-висока степен на производителност. Едно от най-експлоатираните направления, целящи постигането на тази цел, се изразява в прилагане на разнообразни форми на паралелизъм. Формите на паралелизъм се търсят на всички възможни нива: на идейно ниво, на математическо ниво, на алгоритмично ниво, на системно ниво, на структурно ниво, на операционно ниво, на микрооперационно ниво. Но както показва практиката, оползотворяване на издиганите в това направление идеи и подходи е невъзможно да постигнат своята идейна ефективност на 100%. Това се дължи на множество същностно свързани съпътстващи и генерично появяващи се проблеми, в много случаи непредвидени в самото начало. Казаното важи както за софтуерната, но така и за хардуерната реализации. Едно от основните явления, проявяващо се в набелязаното направление, се изразява в появата на невъзможност да бъдат удовлетворени в определени моменти едни или други искания от страна на отделни софтуерни или хардуерни елементи, участващи в изчислителния процес. Причините могат да бъдат различни – ограничения в структурата, недостиг на ресурс, неизбежни латентности, загуба на синхронност, вътрешносхемни състезания, недостиг на време и пр.
В условията на подобен "хаос" и паралелни претенции от страна на източниците, изискващи обслужване, най-евтиното решение, което се практикува, е отказ от паралелизъм в конфликтната точка и организиране на последователно обслужване, но в условията на някаква специална организация, на някакъв ред. Възможностите за налагане на ред са две:
· Редът да се организира въз основа на определена ценностна система, т.е. с въвеждане на приоритет. Ресурсът се предоставя на най-значимия абонат ;
· Редът да се организира въз основа на принципа на състезание във времето, или с други думи, който пристигне пръв, той печели. Смисълът на този принцип не предполага никакъв приоритет. Той се характеризира с пълна асинхронност върху наблюдаваните събития.
Тук ние споделяме разбирането, че арбитрирането е логическа операция изразяваща същността на състезание във времето между настъпващи събития. В резултат на това ще търсим синтез на логическа схема на двувходов арбитър.
Разработени са много стратегии за изграждане на надеждни арбитри, които са се оказали дефектни и са били отхвърлени. Читателят може да се изкуши, и да предложи начини за пристрастяване към едно или друго състояние, така че тригерът да се възстановява от метастабилното състояние в рамките на ограничено време, но такива решения обикновено просто преместват метастабилната точка от едно напрежение в друго, с което не се постига реално подобрение (вижте по-горе фигура 5.5.2.2.4). По подобен начин всеки опит за изграждане на допълнителна схема за откриване и коригиране на метастабилното състояние (например чрез форсиране на нулевото състояние) просто замества една метастабилна трудност с друга, например, такава схема може да реши да причини нулево състояние точно както оригиналният тригер решава да излезе от метастабилното си състояние с преход в състояние 1.
Метастабилното състояние е неизбежна последица от проектните спецификации (изискванията) на арбитъра, и просто няма начин да се избегне изцяло, ако арбитражният проблем наистина трябва да бъде решен. Всъщност тригерите се възстановяват от метастабилни състояния като им се предостави достатъчно време и арбитрите могат да бъдат направени толкова надеждни, колкото се изисква, като увеличат времето, което им е позволено.
Арбитър, който позволява, да речем, няколко стотин наносекунди, за да стабилизира състоянието си (времето зависи значително от прилаганата технологията), намалява вероятността от грешки при синхронизация до порядъка на вероятността за повреда на компонент, което вероятно е поносимо ниво.
Последователностните схеми са абстракция, която изглежда измамно проста за поддържане, тъй като наивният цифров дизайн на циклични вериги с помощта на комбинационни схеми често крие проблемните точки, включващи синхронизация и метастабилни състояния. Дигиталната абстракция е толкова силно вкоренена сред дизайнерите, че мнозина все още не са сигурни, дали един проектиран тригер ще се държи правилно за произволно дълги периоди. В резултат на това проблемът арбитриране едва в последните години, и то с неувереност, се призна за сериозен проблем.
Спецификация
на асинхронен
двувходов
арбитър
Събитията, които се състезават във времето, следва да бъдат поне две. И тъй като метастабилният елемент е бистабилен, за него са характерни две състояния, които могат да се поставят в съответствие на двете входни събития. Както вече беше отбелязано, елементарният арбитър може да бъде някаква схема на метастабилен елемент. Задачата на този елемент е да се установи в едно от двете състояния, характерни за него и съответстващо на входните сигнали, при това по възможно най-бързия начин.
Метастабилната операция, или още самото арбитриране на входните събития, както вече отбелязахме, може да се признае за логическа операция и като такава, да се опише със следващата по-долу логическа таблица. Съответствието на изходите спрямо сигналите на входните събития е посочено в колонката “коментар".
Таблица
1.
Логика на
операция
арбитриране
|
Събития |
Изходи |
Коментар |
||
|
Еvent
0 |
Еvent
1 |
О
0 |
О
1 |
|
|
0 |
0 |
0 |
0 |
Няма
събития,
няма
необходимост
от избор |
|
0 |
1 |
0 |
1 |
Състезанието
във времето
печели
събитие Е1 |
|
1 |
0 |
1 |
0 |
Състезанието
във времето
печели
събитие Е0 |
|
1 |
1 |
1 |
0 |
Победата
се присъжда
принудително
на събитие Е0 |
![]()
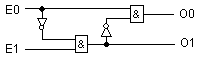
Фиг.
5.5.2.2.7. Логически
функции и
логическа
схема на операция
асинхронно
арбитриране
В
последната
входна
комбинация (11),
която съответства
на
едновременното
появяване на
двата входни
сигнали, се
съдържа
единственото
противоречие
в смисъла на
очаквания
резултат. В
идеалния
случай тази
ситуация е
патова – не
може да се
излъчи единствен
победител,
т.е. решение
няма. Налага
се решението
да се вземе
принудително.
Обикновено
конструкторът
решава в
полза на първото
събитие.
Такова
решение е
реализирано
по-горе в
логическите
уравнения и в
следващата
от тях
логическа
схема (фигура
5.5.2.2.7).
Много
автори, които
са
изследвали
различни
логически,
електронни и
смесени
схеми, са предлагали
свои
формулировки
на параметри,
характеризиращи
метастабилното
състояние на
тези схеми. Въпреки
че
арбитрирането
по същество е
асинхронна
операция, тя
има пряка
връзка с
метода на
синхронно
управление и
продължава
да бъде обект
на
изследване. Освен
времевите
изисквания,
към спецификацията
на
метастабилния
елемент
следва да
бъдат
включени
следващите
три изисквания:
1.
След
появата на
входните
събитията и
веднага след
тяхното
арбитриране,
когато
победителят
е определен,
входовете на
арбитъра следва
да се
затворят за
да се
предотврати
влиянието на
новите
събития. Това
не бива да означава,
че след
затваряне на
входните връзки,
метастабилният
елемент ще се
превключи в
изходно
състояние
(вижте
таблицата
по-горе).
Напротив,
направеният
избор следва
да бъде
съхранен във
времето ;
2.
От така
изказаното
съображение
следва твърде
същественият
извод, че
схемата на
арбитъра
трябва да
притежава
свойството
паметливост.
От тук и следващият
извод –
схемата на
метастабилния
елемент
трябва да
съдържа
тригер. По
смисъла на
така
направените
изводи,
логическата
схема от
фигура 5.5.2.2.7 не
може да бъде
призната за
метастабилен
елемент ;
Много автори твърдят, че арбитрирането е основен феномен на последователни логически схеми, които обработват асинхронни входове. Всъщност тези твърдения не са съвсем ясни. Според нас, както по-горе посочихме, метастабилността е характерна само за системи с обратни връзки. Обратната връзка е основен елемент и обект на изследване в теорията на системите. Обратната връзка също е и инструмент за придаване на определени качества на системите. Така например, благодарение на обратната връзка, при синтеза на логически схеми са създадени схемите на елементарните RS-тригери. Практически обратните връзки се изграждат в електронните схеми, при което параметрите на последните определят и параметрите на метастабилността на дадена схема. Тук трябва да припомним и значението на вътрешносхемните състезания, от които силно зависи крайното състояние на всяка схема. Обратните връзки и метастабилността са причината някои схеми да се възбуждат, при което изпадат в състояние на резонанс – едно състояние, което в определени практически случаи може да бъде много полезно.
Има
научни
публикации, в
които се
твърди, че
маргиналният
вход поставя
бистабилната
схема в метастабилно
състояние, в
което
теоретично може
да остане за
неопределено
време, преди да
премине
към едно от
стабилните
си състояния.
В същото
време са
уверени в
това, че обратните
връзки в
електронната
схема на тригера
винаги
извеждат
схемата от
метастабилното
състояние.
Твърди се
още, че ако
тригерът
попадне в
метастабилно
състояние, вероятността
P
той все още
да е в това
състояние
след време t, може
да бъде
апроксимирана
както следва
![]()
където k и τ са
константи,
които трябва
да се
определят експериментално.
Тази оценка
показва, че вероятността
метастабилността
да се запази
във времето
намалява
експоненциално,
но не
гарантира
ефективността
на тригера при
високи
честоти.
Определянето
на времевите
параметри на
това
състояние е
вероятностен
процес и
изисква
сложно
организиран и
добре
осигурен
експеримент.
Съществува теорема, според която обикновеният Latch RS-тригер е възможно да има неограничена продължителност на това състояние и следва да се приема за нестабилен арбитър. Такива тригери обикновено се използват при изграждане на по-сложни арбитърни схеми. За отстраняване на възможността за резониране, когато схемата е метастабилна, и за да избяга от състояние на метастабилност възможно най-бързо, в проекта на един арбитър обикновено се включва допълнителна мощност. В този смисъл се предлага комбинация от RS-тригер и метастабилен филтър (MUTEX елемент), включени последователно, схема известна като арбитър на Seitz. Като допълнение, последователно към този елемент се употребява още един елемент с подобна функция, така известният Мюлер С-елемент. MUTEX елементът играе ролята на филтър и трябва да има по-ниско прагово ниво спрямо RS-тригера. Например в схемата на 4 битовия асинхронен шинен арбитър 74F786, след входния RS-тригер, съдържа един елемент Exclusive Or и два елемента And. Предлагат се още различни усложнени логически схеми на двувходов арбитър с последователно свързани структурни елементи, като асинхронни Latch RS-тригери, Latch или Edge D-тригери. Достига се дори до два последователни Edge D-тригера. Вече обърнахме внимание на факта, че метастобилността може да се провокира и от не достатъчно високото ниво на входния сигнал, т.е. от това, че той не съвсем категорично удовлетворява стандарта, за да бъде признато неговото ниво за логическа стойност. Желанието е да се запази изходната стойност постоянна, докато входният сигнал не се отклони достатъчно от междинно метастабилно ниво към стандартното цифрово ниво и така да се осъществи бърз преход на крайния изход. Обобщението е, че в практическите реализации метастабилността трябва да бъде определена за ограничен интервал от времето. По ред причини обаче интервалът, в който може да се появи метастабилност, не може да бъде сведен до нула. Според нас, в интерес на арбитрирането е, той да бъде максимално минимизиран, което ще направи арбитъра чувствителен.
3.
И накрая,
но не на
последно
място, е
следното
съображение:
след
арбитрирането
арбитърът
съхранява
направеното
отсъждане. За
да се състои
обаче
следващото
арбитриране,
арбитърът
трябва да
бъде приведен
в изходно
състояние,
което изисква
нулиране на
запомнящия
елемент в
неговата
схема. Според
първото
съображение
на тази
спецификация,
възстановяването
на изходното състояние
на арбитъра
означава
отваряне на
неговите
входове с
разрешен
достъп на събития.
Тук следва да
поясним
възможните ситуации
относно
събитията
към този
момент.
Възможностите
са две:
·
Да са
налични
събития,
които са
настъпили до
този момент и
техните
сигнали вече
са
достигнали
входовете на
арбитъра ;
·
Все още
събития не са
настъпили и
сигнали на
входа на
арбитъра
липсват.
При
първата
ситуация
следва да
разбираме, че
последващото
арбитриране
по същество е
безсмислено,
тъй като при
нея е
нарушена логиката
на операция
арбитриране
в смисъла на
възприетия
тук ред. Все
едно да
търсим
победител,
след като
всички
състезатели
са пресекли
финалната
линия. Тази
ситуация не е
нормална за
асинхронния
арбитър и
може да се определи
като
състояние на
насищане. За
това е
виновен
ресурсът,
който
арбитъра
обслужва. Ето
защо би
следвало да
се работи за
повишаване
на неговата
производителност.
Ако все пак
установяването
на арбитъра в
изходно
състояние
заварва
множество
вече състояли
се събития,
то по силата
на тази патова
ситуация,
победата ще
бъде
присъдена на
събитието с
най-малък
номер.
Установяването на арбитъра в изходно състояние по същество е старт за следващото арбитриране. Казаното е пояснено със следващата примерна времедиаграма.

Фиг. 5.5.2.2.8. Представа
за процеса на
асинхронно
арбитриране
Арбитър.
Анализ и
синтез на
логическа
схема с RS Latch
тригер
Изхождайки от разбирането, че арбитърът трябва да определи победителя в състезанието между две събития (Event), ще формулираме проектните му концептуални спецификации (изисквания).
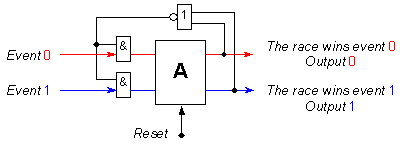
Фиг. 5.5.2.2.7. Постановка и място на арбитъра
И така, схемата на арбитъра има два входа, на които, за своето настъпване, двете събития изпращат преден фронт на правоъгълен сигнал. Арбитърът има за задача да определи кой от двата фронта се е появил първи на вход, т.е. кое събитие печели състезанието. В изходно състояние арбитърът очаква появата на сигнали за настъпили събития. В това състояние той следва да се установи и след подаване на сигнал Reset. Изходното състояние се характеризира с нулеви изходни сигнали (Event 0 = 0, Event 1 = 0). След акта на арбитриране на един (и само на един) от изходите на арбитъра се установява единица, с което той показва, че съответният входен сигнал е спечелил състезанието. С други думи на изходите на схемата не са възможни едновременно две единици. От схемата се вижда, че след акта на арбитриране, сигналът на обратната връзка затваря входните схеми И. Нов акт на арбитриране може да бъде осъществен след привеждане на арбитъра в изходно състояние. В това състояние входовете на арбитъра са разрешени за постъпване на сигнали.
Арбитърът установява стойност единица (1) на принадлежащия на съответното събитие изход. На изхода, принадлежащ на събитието, загубило състезанието, се установява стойност нула (0). Една разумна проектна спецификация може да изисква следните условия:
· Входът за нулиране на арбитъра (Reset) заставя и двата му изхода да се установят в състояние нула 0, в което остават, докато не се появят един или и двата входни сигнала. Това практически е изходното състояние ;
· Появата на един или и на два входни фронта (Event 0, Event 1, (E0, E1)) води след интервал от най-много от td (delay, закъснение) секунди точно един от изходните линии да се установи в състояние 1, а другият да се установи в състояние 0. Тези нива на изходите се запазват до следващия сигнал за нулиране на арбитъра. През това време е забранено постъпването на други входни сигнали, както и тяхното изменение ;
· Ако се появи преден фронт на сигнал Е0 и той остане активен в продължение на tNM (by Narrow Margin, с малка разлика) секунди или повече преди да се появи преден фронт на сигнал Е1, тогава състезанието печели събитието Event 0 (The race wins event 0 = 1, Output 0 = 1). Изходът Output 1 ще остане в състояние 0 (Output 1 = 0).
Аналогично, ако се появи преден фронт на сигнал Е1 и той остане активен в продължение на tNM секунди или повече преди да се появи преден фронт на сигнал Е0, тогава състезанието печели събитието Event 1 (The race wins event 1 = 1, Output 1 = 1. Изходът Output 0 ще остане в състояние 0 (Output 0 = 0) ;
· Ако предните фронтове на сигналите E0 и E1 се появят едновременно или най-много точно на отстояние tNM секунди един от друг, тогава на един от изходите - не ни интересува кой - ще бъде ще се установи валидна стойност 1, а на другия ще се установи валидна стойност 0.

Фиг. 5.5.2.2.8. Почти едновременност
Това ще се случи след td секунди. С други думи, спечелването на състезанието между двете събития все пак ще бъде присъдено на едно от събитията. Изборът между двете събития в този случай ще се дължи на вероятното поведение на метастабилността на схемата.
Латентността на арбитъра td следва да бъде избрана така, че да отразява реалните закъснение на логическите елементи на схемата и вземането на приемливо решение от нейна страна. Времето за арбитриране tNM позволява възможност за грешка при извършване на “фото-финиш". Така при близки състезателни резултати се допуска да бъде взето произволно решение. При подходящи стойности за параметрите td и tNM арбитърът изглежда достатъчно конструктивен. Например, двойка RS-тригери могат да бъдат свързани така, щото да бъдат установявани от единия Event-вход и едновременно да деактивират другия вход.
Проблемът с асинхронния арбитър се корени в това, че входните променливи се разглеждат в нашия дискретен модел като непрекъснати величини. В крайна сметка за начален анализ се предлага следната логическа схема на арбитъра.
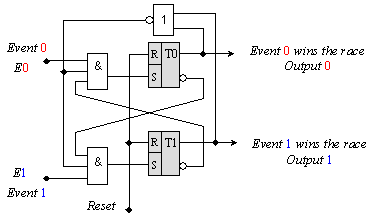
Фиг. 5.5.2.2.9. Първоначална логическа схема на арбитър.
Входовете (Event) са предназначени за логически нива, които обикновено носят сигнал с ниско ниво (логическа стойност нула 0), но се превключват в логическа стойност единица 1 при настъпване на съответното събитие. Линията Reset служи за нулиране на двата Latch RS-тригера, така че на правите им изходи се установява логическа стойност нула (0), а на инверсните им изходи – единица (1). При пристигане на който и да е от предните фронтве на сигналите E0 или E1, съответният тригер е свързан така, че неговият прав изход се установява в логическа стойност 1. Съответно, на инверсния му изход се установява логическа стойност 0, която по обратната връзка затваря входната врата на другия сигнал. Тъй като входните процеси са асинхронни, то е напълно възможно те да се явят едновременно или с минимална разлика (приехме не повече от tNM), която е по-малка от латентността td на арбитъра. Така в крайна сметка ще бъдат избрани двама “победители", което е недопустимо според приетите спецификации.
Този анализ показва, че предложената логическа схема може да се определи за наивно синтезирана!
За да се отстрани изявената некоректност, схемата е ревизирана, както е показано по-долу.
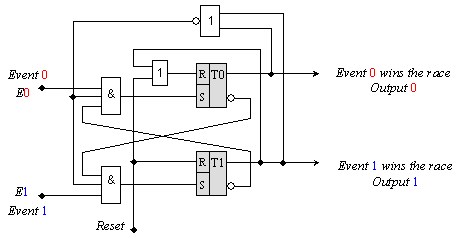
Фиг. 5.5.2.2.10. Подобрена логическа схема на арбитър.
Въведена е обратна връзка от правия изход на тригер Т1 към вход R на тригер Т0, с което се гарантира наличието на изходите на арбитъра само една единица или две нули. Така, ако се появи описаната по-горе ситуация, за победител винаги ще се определя сигнал Е1.
През повечето време (след сигнал Reset) тригерите в схемата ще се намират в нулево състояние. Но съществува неизбежната възможност кратък пулс импулс с точно правилната продължителност да изпрати схемата в крайното състояние, между двете стабилни състояния. Явлението се нарича метастабилно състояние и е резултат от липсата на синхронизация между двата входни процеса, което от своя страна приемаме за невъзможно, тъй като противоречи на началната концепция и смисъла на състезанието.
На практика, сигналите от тип Event, се оприличават най-често на сигнали от тип Request, т.е. заявки от определени източници за събития, които изискват бърз отговор или някакво последващо незабавно обслужване. Изходните сигнали от своя страна са предназначени в отговор да уведомят предпочетения, в смисъла на операцията арбитриране, източник. В този смисъл изходните сигнали от тип Output се оприличават обикновено на сигнали от тип Acknowledgement, Confirm или Grant, които имат смисъла на потвърждаващи, разрешаващи или одобряващи следващите действия, които ще предприеме съответно посочения източник.
Трябва
да се
съгласим с
положението,
че това
изразява
същността на
асинхронните
цифрови
системи и на
асинхронния
цифров
дизайн.
Проблемите,
които причинява
асинхронността
не са
непреодолими,
но те
въвеждат
допълнителни
апаратни
разходи и
ограничения
на
производителността,
които от своя
страна
влияят на
организацията
на системите
като цяло по
съществен
начин и по-специално,
те
ограничават
нивото, до
което асинхронните
техники
могат да
бъдат използвани
на практика.
Арбитър.
Синтез с
комбинационна
логическа
схема
Вече
повече от 40
години
синтезирането,
изследването
и
практикуването
на логически
схеми
показва
силната си
зависимост
от реалното
поведение на
последните. Счита
се, че
арбитрирането
е основен
феномен на
последователностни
логически
схеми, които
обработват
асинхронни
входове.
Реалността в
последователностните
логически
схеми се
характеризира
с
вътрешносхемните
състезания,
явление,
което често
наричат хазарт.
За
логическите
схеми с
обратни
връзки обаче
това
твърдение не
е съвсем
точно. Според
нас
метастабилността
е характерна
само за
системи с
обратни
връзки.
Обратната
връзка е
основен
елемент и
обект на
изследване в
теорията на
системите.
Обратната
връзка също е
и инструмент
за придаване
на
определени качества
на системите.
Ето защо,
такива елементарни
схеми като
например RS-тригерите
или даже така
нареченият Muller C-елемент, които
много автори
използват
като метастабилен
елемент, не
могат да се
приемат като последователностни
схеми.
За
латентностите
на
логическите
елементи, за
вътрешносхемните
състезания,
за преходните
процеси в
логическите
схеми, за временните
неистинни
логически
нива на изходите
им и още
много други
ефекти, които
не могат да
бъдат
изразени от
логическите
функции, са
написани
множество
публикации. С
продължаващия
напредък в
дигиталната
технология и
нарастващата
сложност на
системите с
мащабен
паралелизъм,
особено в тези,
които
интегрират
над един
милиард транзистора
в чип, силно
нараства
вероятността
за поява на
много
високочестотни
асинхронни
взаимодействия,
които могат
да доведат до
чести откази.
Така с
годините
асинхронната
природа не
можеше вече
да бъде
заобикаляна,
тя трябваше
да бъде
забелязана и
взета под внимание,
което
представлява
същността на
съвременното
състояние в
дигиталния
дизайн.
Асинхронните
методи за
дизайн
доведоха до
появата на
изключително
оригинални и
полезни
решения. Едно
от
интересните
явления,
което се
оказва
полезно в
светлината
на разглежданата
тук тема, е
метастабилността
на логически
схеми с
обратни
връзки. Метастабилното
състояние е
онова състояние,
в което се
оказва всяка
система,
която в
момента,
когато
трябва да
направи своя
избор, се
сблъсква с
Хамлетовия
въпрос: “… to
be, or not tot be”.
В
повечето
научни
публикации и
в учебната и
в
популярната
литература на
метастабилността
се гледа като
на негативно
и опасно
явление,
водещо до
откази в
логическите
схеми. Ще
цитираме
мнението на
В. И.
Варшавский,
който
отбелязва: “Арбитражният
проблем
възниква
независимо
от
естеството
на процесите
и споделения
ресурс. Дори
и да е софтуер,
проблемът в
крайна
сметка се
свежда до
изграждането
на работещ
хардуерен арбитър".
Разбира се в
определени
случаи този
негативизъм
е оправдан,
но ние
определено
считаме, че
дълбокото
познаване на
явлението
води до изява
на неговата
полезност. А
полезността
се изразява
във
възможността
за бърз,
лавинообразен
и
безвъзвратен
избор на едно
от крайните
състояния,
отговарящо на
моментната
входна
реалност. И
тук случаят е
точно такъв –
направеният
от нас анализ
позволи
формулирането
на
спецификация
за синтез на
метастабилен
елемент,
изложена по-горе,
и
превръщането
му в градивна
схема на двувходов
асинхронен
арбитър.
Отчитайки
анализа на
операция
арбитриране,
както и споменатата
по-горе
спецификация,
тук предлагаме
още една нова
и оригинална
схема за нейната
техническа
реализация.
Последната
се основава
на
синтезираните
за нея
логически
функции и
тяхната
схема,
представени
на фигура 5.5.2.2.7.
Комбинационната
арбитражна
схема е
допълнена с
два
асинхронни Latch RS-тригерa,
които
удовлетворяват
изискванията
на
спецификацията,
осигурявайки
свойствата
паметливост
и
управляемост.
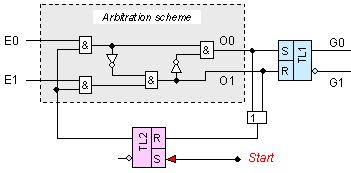
Фиг.
5.5.2.2.11. Логическа
схема на
2-входов
асинхронен
арбитър
Свойството
паметливост
арбитърът
получава чрез
асинхронния
тригер TL1.
В обратната
връзка е
поставен
тригер, който
забранява
двете входни
линии
веднага след
направения
избор. Тригер
TL2
осигурява на
заявения
ресурс
възможността
да управлява
арбитъра,
като разрешава
чрез строб
сигнала Start
следващото
арбитриране
в
необходимия
за него
момент. Преди
всяко ново
арбитриране тригер
TL1
трябва да
бъде
принудително
нулиран, което
означава
подаване на
строб сигнал Reset (не е
показан на
схемата)
преди сигнал Start.
Изборът
на
арбитражната
схема (O0,O1) има
латентност,
която ще
означим ( tAS ). Той
се записва в
тригер TL1 и
излиза на
изход (G0,G1)
със
закъснение ( tTL1 ). Така
минималното
закъснение
между двата входни
сигнала (E0,E1), което
определя
чувствителността
на арбитър, е
равно на
сумата
( tAS + tTL1
).
Следващата
логическа
схема, която
предлагаме,
представена
на
следващата
фигура, е оптимизирана
към по-висока
чувствителност
на
арбитриране.
Изходите (G0,G1)
получават
своите
логически
стойности по изпреварващите
тригер TL1
връзки,
директно от
изходите на
арбитражната
схема (O0,O1).
Освен това
затварянето
на входовете
на арбитражната
схема също се
извършва
изпреварващо
във времето
чрез
инвертора,
включен
паралелно на
тригер TL2.
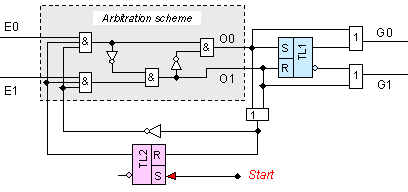
Фиг.
5.5.2.2.12. Логическа
схема на
чувствителен
2-входов асинхронен
арбитър
При
така
добавените
връзки
закъснението
на
осъществения
от
арбитражната
схема избор (G0,G1)
оценяваме
със сумата ( tAS + tOR ), където с ( tOR ) е
означена
латентността
на
логическия елемент
ИЛИ. Уверено
можем да
твърдим, че
сумата ( tAS +
tTL1 ) е
съществено
по-голяма от
сумата ( tAS +
tOR ).
Подобна е
оценката за
скоростта, с
която се
затварят
входовете на
арбитражната
схема от
фигура 5.5.2.2.12.
Въз основа на горните констатации, можем да изтъкнем следните положителни характеристики на предложената логическа схема на 2-входовия асинхронен арбитър:
1.
Тя е
възможно
най-бързата –
латентността
ѝ е сравнима
със
закъснението
в
превключването
на
комбинационната
арбитрираща
схема. Това я
прави
възможно
най-чувствителната
по отношение
на
изоставането
във времето
на едното от входните
събития
спрямо
другото ;
2.
Тя е
по-икономична
от
представената
на фигура 5.5.2.2.10.
Арбитриране
на повече от
две събития
Случаят с арбитриране на две събития е само едно начало, изразяващо същността на проблема, т.е. дефиниращо го. Практиката обаче може да създаде значително по-сложни ситуации, като например, арбитриране на повече от две събития. На пръв поглед това е напълно възможно, но синтезът на практическото решение не е никак лесен.
Първата идея, върху която ще търсим практическо решение, се основава на последователното арбитриране на следващото (трето) ново събитие с победителя от първоначалните две. Ще получим следната схема с три входа и три изхода, като само на един от тези изходи е възможна единица.
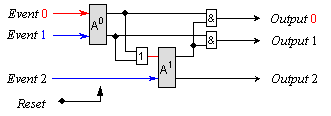
Фиг. 5.5.2.2.13. Схема на 3-входов последователен арбитър
Виждаме, че на горния вход на втория арбитър се подава обединението на изходите от първия арбитър. Това е така, защото изходната комбинация от дву-входовото арбитриране, може да съдържа само една единица (10 или 01). В последствие, ако вторият арбитър посочи за победител събитието, което му е подадено на горния вход, окончателната конкретизация се осъществява от включените паралелно логически елементи И. Така на изходите на арбитъра са възможни три комбинации с една активна единица – 100, 010 или 001.
Към входното множество събития добавяме още едно и прилагаме същата идея. Единственият възможен победител от 3-входовото множество обединяваме в 3-входовия елемент ИЛИ и подлагаме на арбитриране с новото събитие E3. Така достигаме до следващата логическа схема. Победителят от четирите входни сигнали е само един, което означава, че на изход са възможни единствено следните комбинации – 1000, 0100, 0010 или 0001.
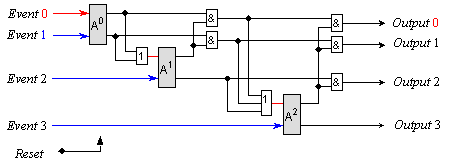
Фиг. 5.5.2.2.14. Схема на 4-входов последователен арбитър
След аналогични съждения се достига до следващата логическа схема на 5-входовия арбитър.
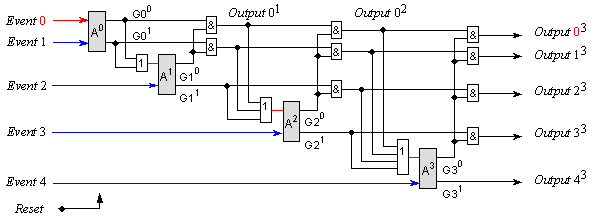
Фиг. 5.5.2.2.15. Схема на 5-входов последователен арбитър
Следвайки последователния синтез на представените логически схеми по индукция стигаме до извода, че всяка от степените на арбитъра може да се изрази със следните общи уравнения.
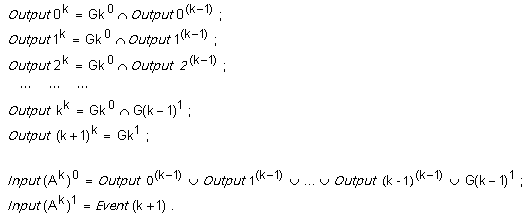
Възможността да бъде изразен общият случай на логическата схема налага извода, че подходът е универсален и синтезът на логическата схема на арбитър с произволен брой входове е гарантиран.
От логическата схема разбираме, че всяко следващо събитие се състезава с победителя от всички предидущи събития. На изходите е възможна само една единица, т.е. победителят е един. Неговият номер е непосредствен, но може да бъде шифриран във вид на цяло число.
Основният недостатък на показаната схема е последователното увеличаване на латентността на междинните резултати, което може да доведе до изкривяване на крайния резултат за събитията с по-големи номера. По тази причина е редно да се потърси схема за паралелно арбитриране на събитията.
За по-задълбочени познания по темата читателят следва да се запознае с научните публикации, като една от достатъчно обхватните е книгата на Дейвид Кинимент:
David J. Kinniment, Synchronization
and Arbitration in Digital Systems, John Wiley & Sons Ltd, 2007, ISBN
978-0470-51082-7, pp. 274.
Внимателният читател вероятно вече е забелязал анонсирането на следващата идея, върху която ще търсим практическо решение за арбитриране на повече от две събития. Същността се състои в едновременното арбитриране на наличните събития, така както в спорта, при еднакви начални условия, стартират и се състезават няколко спортиста едновременно. Като за начало, при наличие на двувходова схема за арбитриране, за нас е естествено да формираме и анализираме една начална група от 4 въпросни събития, които е възможно да бъдат обхванати само с две еднакви схеми за арбитриране. Така ще трябва да търсим схема с 4 входа и 4 изхода, реализирана с помощта на двувходовия арбитър, с който разполагаме, в качеството му на градивен елемент, показан по-горе на фигура 5.5.2.2.10.
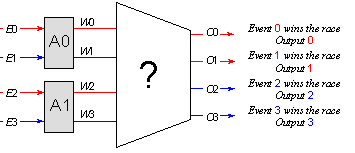
Фиг. 5.5.2.2.16. Организация на 4-входово паралелно арбитриране
Тъй като излъчените от първите двойки победители са напълно независими, то следва те да бъдат подложени на съвместно арбитриране. Възможните съвместни комбинации от стойностите на изходните сигнали W0, W1, W2 и W3 са сведени в следващата таблица.
|
W0 |
0 |
0 |
1 |
1 |
|
W1 |
1 |
1 |
0 |
0 |
|
W2 |
0 |
1 |
0 |
1 |
|
W3 |
1 |
0 |
1 |
0 |
Посочените 4 комбинации са взаимоизключващи се, т.е. възможна е първата, ИЛИ втората, ИЛИ третата, ИЛИ четвъртата. Това ни навежда на идеята за възможно съвместно арбитриране на двете двойки, което в същност се и преследва. Победител (със свой състезател) се явява една от двойките. Последващото разпознаване на конкретния състезател Е0, Е1, Е2 или Е3, ще осъществим чрез дешифриране, което ни води до окончателната схема, показана на следващата фигура.
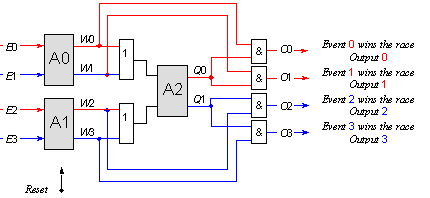
Фиг. 5.5.2.2.17. Схема на 4-входово паралелно арбитриране
Възможностите за увеличаване на броя на паралелните входове са няколко, от които ние тук най-напред ще разгледаме тази, която се изразява в двойното им увеличение. Анализът на двете паралелни половини на нивото на изходите на вторите арбитри Q0, Q1, Q2 и Q3 изявява аналогичната зависимост, която беше установена в предходната схема и е изразена със съответната таблица. Така синтезът ни води до следната логическа схема на 8-входовия арбитър.
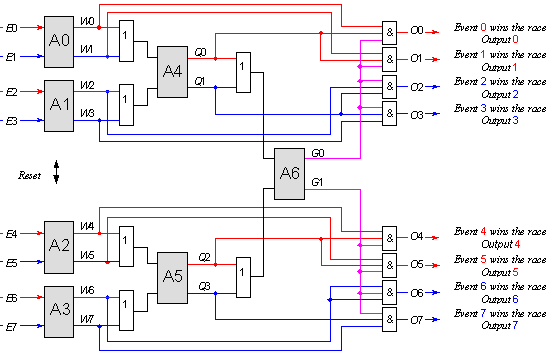
Фиг. 5.5.2.2.18. Схема на 8-входово паралелно арбитриране
От получената логическа схема се вижда, че тя има тристепенна структура. По-нататъшното увеличаване на броя на входовете на арбитъра може да продължи по различни начини. Например, може да бъде добавен един нов сигнал, или два, а може да увеличим броя на входовете двойно (до 16), следвайки вече възприетия подход. Ако увеличим броя на входовете до 16, структурата на логическата схема ще се нуждае от още един двувходов арбитър А7. Може да се твърди, че по отношение на неговите два входа, комбинациите от изходите на предходната степен G0, G1, G2 и G3, са също така взаимно изключващи се, както тези от изходите Q и W на предидущите степени. Така може да обобщим и да твърдим, че взаимоизключването на комбинациите от изходите на предходната степен във всяка нова степен на арбитъра е принципно и е в сила за всякакъв брой новодобавени входове в схемата на арбитъра. Този принцип прави синтезът на логическата схема на арбитър с произволен брой входове универсален.
Синтезираният
многовходов
асинхронен арбитър
с паралелно
присъединяване
на входните
събития е
едно
усъвършенствано
продължение
на арбитъра с
последователно
присъединяване.
Той е по-бърз
и това лесно
се показва – в неговата
8-входова
логическа
схема има само
3
последователни
нива, срещу 7 в
сравнявания
арбитър. С
увеличаване
на броя на
входовете
разликата
нараства в
полза на представения
тук арбитър.
В общия
случай имаме
следните
количествени
оценки,
сведени в
следващата
таблица.
Приведените
количествени
оценки могат
да помогнат
за качествена
оценка на
сравняваните
арбитри. Обобщението
се
осъществява
чрез
параметъра k,
който приема
за стойности
цяло число
без знак,
различно от
нула – (k>0,
k≠0).
|
Брой на входовете |
Присъединяване на входове |
Брой на 2-входовите арбитри |
Брой на степените |
|
|
Последователно |
|
|
|
|
Паралелно |
|
k |
Синтез на
бързи
многовходови
асинхронни арбитри
За да бъде запазена скоростта за арбитриране при многовходовите арбитри не бива да се допуска последователно използване на градивната схема в логическата структура на абитъра. Това е възможно да се осъществи единствено при пълно комбиниране по двойки на входните събития. Така например, за 4-входов арбитър следва да бъдат реализирани следните комбинации: (0-1), (0-2), (0-3), (1-2), (1-3) и (2-3). Всяка комбинация се арбитрира от собствен 2-входов арбитър. За да бъде избрано дадено събитие, то трябва да бъде победител при арбитрирането с всяко от останалите събития. Следвайки тази логика стигаме до следващата логическа схема.
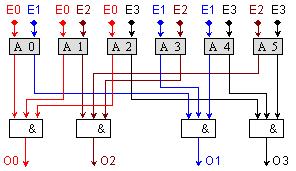
Фиг.
5.5.2.2.19. 4-входов
асинхронен
арбитър
Добавянето на входно събитие към наличните до момента събития се подчинява на вече създадената логика. Така например, ако към разгледаното по-горе множество от събития добавим още едно (E0, E1, E2, E3, E4), ще създадем следната логическа схема.
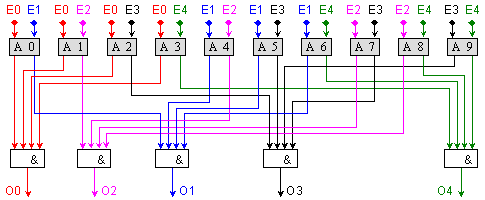
Фиг.
5.5.2.2.20. 5-входов
асинхронен
арбитър
Арбитрирането определяме като логическа операция, изпълнявана от метастабилния елемент А, който вече определихме като градивен елемент за многовходовите арбитри. Тази операция няма математическо означение и за да можем да изразим аналитично логическата функция на всеки изход на многовходовия арбитър, ще въведем означението (<≡). Основният символ в това съчетание е символът на съответствието (≡). С помощта на символа (<) искаме да посочим кое е събитието, което операцията арбитриране е избрала или посочила в конкретната комбинация. Така изразът
![]()
следва да означава, че спечелилото събитие е Ei. Ето и общия вид на произволна изходна функция.
![]()
![]()
Както
се вижда,
това е
конюнкция от
всички едноименни
събития,
спечелили
състезанието
по
възможните
двойки
събития.
Изразът на
конюнкцията
съдържа две
части. В
първата част
дадено
събитие Ei се
сравнява с
всички останали,
следващи
позицията i, а във
втората част
– с всички
предхождащи
позицията i.
В
многовходовия
арбитър
всички
градивни арбитри
функционират
паралелно
във времето.
Така
латентността
на всеки
такъв многовходов
арбитър е
равна на тази
на единичния
градивен
елемент. Това
прави
предлаганата
логическа
структура
възможно
най-бързата.
Казаното
обаче се
отнася само
за случая,
когато целта
е определяне
единствено
на победителя
в цялото
множество
събития.
Както обаче
вече
пояснихме,
съществуват
приложения, в
които е
необходимо
да се
използва
закъснението
между
отделно
подредените
в състезанието
събития
(втори, трети
и пр.). В такива
случаи може
да се
определи
закъснението
между първия
и последния
участник в
състезанието,
както и между
победителите
в отделните комбинационни
двойки. Това
е възможно да
бъде необходимо,
когато за
отделните
ресурси е важно
да избират
момента, в
който следва
да бъде
издаван
стробът Start.
Броят на двувходовите градивни арбитри, необходими за логическата схема на n-входов комбинативен арбитър, може да се определи с помощта на следната формула:
![]()
Въпреки че на представените логически схеми не е изобразен управляващият строб Reset, той следва да бъде реализиран във всеки градивен елемент, а оттам, като обединен, той ще присъства в схемите на всеки многовходов арбитър.
Необходимо е да поясним още, че поради закъсненията във времето на входните сигнали, отделните градивни елементи ще осъществяват своя избор в различни моменти от времето. Това означава, че автоматичното затваряне на входовете на отделните градивни арбитри, също ще се извършва в различни моменти. Това обаче не може да попречи на функционирането на арбитрите.
Арбитриране
в условия на
суперскаларност
Както беше указано в началото, съвременната реалност се характеризира с множество форми на паралелизъм. Най-ранната се изразява в конвейерна организация на изчислителните структури. Следващата форма е суперскаларната, към която е насочен нашият интерес тук. Въвеждането на повече от един еднакъв по функция и строеж елемент (ресурс) в структурата на изчислителната система винаги е правено с надеждата, че това ще я направи по-производителна. В много случаи това е така. В сложните системи обаче това не е съвсем така, което е свързано с възникването на нови и специфични проблеми, отнасящи се до управлението на тази суперскаларност.
Във връзка с разглежданата тук тема, арбитрирането на събития, които се отнасят до ресурс, работещ е в условия на суперскаларност, се изявява като нов и неизследван проблем. Следва да отбележим, че за възникващите събития, броят на клонингите на ресурса, към който те се стремят, е неподозиран, а и той е без значение, стига да се “докопат” до него, или от наша гледна точка – до един от многото екземпляри.
Арбитрирането на идващите във времето събития ще изяви първия победител, който е редно да ангажира един от клонингите на ресурса, който условно можем да наречем "първи". С това обслужването на искането на първото събитие стартира. Вторият клонинг на ресурса все още е свободен и очаква избора на своето събитие. Така вече имаме за задача да изберем второто в състезанието събитие. След като отделим първото събитие, което вече е определено, можем да определим второто събитие като първо измежду останалите, т.е. без първото . Това е възможно да стане с клонинг на същия арбитър, условно наречен “втори" арбитър. Вторият арбитър ще определи победителя измежду останалите състезаващи се събития, който по отношение на първото събитие, ще бъде втори. Условието е вече избраното събитие да бъде изолирано от останалите и да не участва в състезанието. Така спечелилото събитие ще бъде насочено за обслужване от втория клонинг на ресурса. Описаната логика е илюстрирана на следващата фигура.
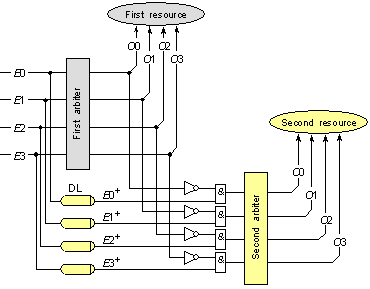
Фиг. 5.5.2.2.21. Логическа структура с дублиран ресурс
На рисунката се виждат двата клонинга на ресурса и на многовходовия арбитър. Събитията постъпват и към двата арбитъра. Изключването на по-ранно избраното събитие от арбитриране се постига с логически елемент И, забранен от инверсията на самото събитие.
Интересното в представената структура са симетричните закъснителни линии DL. Тяхната задача е разбираема – те са длъжни да задържат във времето всяко едно входно събитие, като по този начин ще отчетат латентността на избора в първия арбитър. Работата на втория арбитър е аналогична. Избраното от него второ по ред в състезанието с времето събитие естествено ще забави на време τDL стартирането на работата на втория ресурс, но такива са реалностите на съвременния хардуер. Техническата стойност на латентността на закъснителните елементи зависи от сложността на логическата схема на арбитъра и определянето ѝ е задача на проектанта.
Ако се налага, описаният подход може да се приложи аналогично за следващи нива на логическата структура.
Определяне
на финалните
закъснения и
логическа
структура за
реализация
Ще
анализираме
най-съществената
част от състезанието
на събитията
в подхода им
към финала.
Завършващата
част от
процеса е илюстриран
на фигурата
по-долу,
където са
изобразени
назад във
времето
закъсненията
на отделните
събития
спрямо
финалния
момент на
победителя (събитие
E4).
Рисунката
изобразява
най-съществената
част от
времевия
процес –
разсейването
на движението
на събитията
във времевия
интервал на
финализация (TLIE).
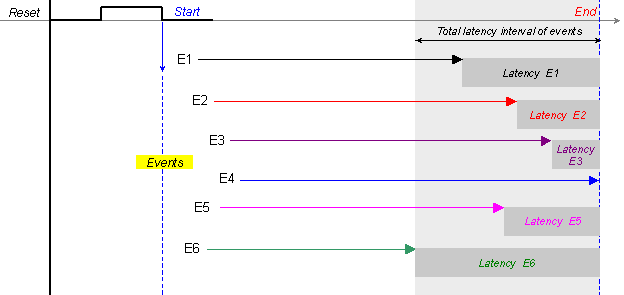
Фиг.
5.5.2.2.22. Интервал
на
разсейване
на събитията
във времето
преди финал
Изобразени
са
закъсненията
на отделните събития
E1, E2, … , E6 относно
базовия
момент End, назад във
времето. За
интервала TLIE може да
се каже, че
той не е
постоянен и
може да бъде
както много
тесен така и
достатъчно
широк, което
зависи от
структурните
елементи в
системата,
формиращи и
издаващи сигналите
E1, E2, … , E6.
Конструкторът
на системата
е този, който
е в състояние
да влияе на
този
интервал при
необходимост.
Във всички
случаи той
влияе на
общата
честота на циклическо
повторение
на основните
функции на
системата.
Съществуват
системи, в
които се
използват
под някаква
форма оценки
на тези
латентности.
По този начин
се формират
числени
параметри на
системата, които
се използват
в
последствие
за нейното
адаптивно
управление.
Ето защо тук
ще предложим
една
възможност
за измерване
на
продължителността
на отделните
закъснения.
Примерното
решение,
което
предлагаме
по-долу
(фигура 5.5.2.2.23), се
основава на
логическата
структура за
определяне
(излъчване)
на поредноста
на събитията
в тяхното
последователно
подреждане
назад във
времето, пояснена
по-горе, във
връзка с
обслужване
на дублирани
изчислителни
ресурси.
Решението
на
изследвания
тук проблем е
конкретно за
проследяване
само на 4 от
събитията (E1, E2, E3, E4), което е
достатъчно
за да може по
индукция да
бъде
съобразена
необходимата
структура
при повече
събития. В
него са
използвани 4
арбитъра (A1, A2, A3, A4),
включени
последователно,
върху
съответно
последователно
задържаната
във времето съвкупност
от входни
сигнали (E1, E2, E3, E4).
В
логическата
структура за
измерване на
времевите
интервали се
използва
еталонен тактов
генератор (Etalon Clock Generator - ECG). Генерираните
последователно
еталонни периоди
се отброяват
в броячите CLEi (Country Latency Events). Отброяването
се разрешава
в момента, в
който от
първия
арбитър бъде
определен
сигналът на
първото
събитие, т.е.
на
спечелилото “състезанието” събитие. Може да се
проследи как
от този
момент нататък
сигналите “+1”
започват да
постъпват
едновременно
във всички
броячи. Този
момент
съответства
на времевата
база “end”,
определена,
както е
изобразено
на фигура 5.5.2.2.22.
Отброяването
в отделните
броячи CLEi
се
преустановява
(забранява)
съответно от изходните
сигнали (O2, O3, O4), както
те са
разпознати
във времето. В
представената
логическа
структура не
са
изобразени
управляващите
сигнали Reset и Start.
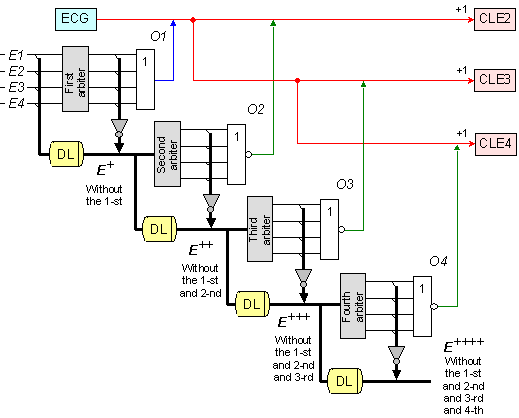
Фиг. 5.5.2.2.23. Структура за измерване на финалните латентности
Така представеното на горната фигура решение обаче страда от един недостатък. Той се изразява в това, че броячите CLEi измерват латентностите на второто, третото, четвъртото и пр. събития, но в смисъла на съответната им подреденост при достигане на “финала”. Подредеността на финиширане обаче по никакъв начин не идентифицира събитието като принадлежащо на съответния източник, който го е генерирал. Това ясно може да се забележи от рисунката на фигура 5.5.2.2.22. На нея се вижда следната подредба: LE3 < EL2 < LE5 < LE1 < LE6. С други думи, например, събитие E1 финишира 5-то по ред и неговото закъснение ще бъде измерено от брояч CLE4. Идентификацията, че стойността в брояч CLE4 се отнася за събитие E1, а не за някое друго, изисква към изхода на съответния арбитър (в случая A5) да бъде подключен шифратор.
Следващият
раздел е:
5.5.2 Шини. Синхронен и асинхронен обмен. Арбитриране на шинния обмен – Продължение 3