Този раздел е нов. Създаден е през 2021 година.

3.1.1. Схеми с паметливост. Промишлени схеми. Допълнение

Въведение в схемите с паметливост

Схемите, притежаващи свойството паметливост най-общо могат да бъдат причислени в две големи групи:

· Схеми с динамична паметливост и ;

· Схеми със статична паметливост.

Паметливите схеми, с които се занимаваме в областта на цифровото инженерство, се определят като дву-стабилни или още би-стабилни. Би-стабилните електронни вериги имат две стабилни работни състояния - състоянието, при което на извода, определен като “изход", се наблюдава логическа единица “1”, и състоянието, при което на извода, определен като “изход", се наблюдава логическа нула “0”. Когато би-стабилната схема се намира в едно от тази двете стабилни състояния, е необходимо известно количество енергия, за да бъде тя извадена от даденото състояние и да влезе в другото, противоположно стабилно състояние. По време на прехода между състоянията изходният сигнал следва да се придвижи през регион, където той е нестабилен. Паметливите схеми следва да са проектирани така, че да не могат да останат в нестабилно състояние, при това за неопределено време. След като навлязат в преходната област на нестабилното състояние, те веднага се опитват да възвърнат (да преминат) едно от двете стабилни състояния. Ето защо този преход се определя като лавинообразен. Той трябва да бъде възможно най-кратък, т.е. преходът (превключването) трябва да бъде високо скоростно, което по този начин определя така известното бързодействие на схемата.

Следващата фигура илюстрира казаното по-горе. Топчето може да се намира в стабилно състояние или отляво на възвишението (състояние, условно отбелязано с “0”), или отдясно на възвишението (състояние, условно отбелязано с “1”). За да придвижим топчето от едната страна към другата, трябва да прехвърлим нестабилната област. За целта е необходимо определено количество енергия. В тази аналогия съществува трето потенциално стабилно състояние, в което с точното количество енергия би било възможно да се балансира топката точно на върха на възвишението. Това състояние се нарича метастабилно. То е междинно състояние и в този смисъл не е полезно, тъй като не може да се признае за логическо. За неговото преодоляване е важно да се гарантира, че подаваната на вход енергия е достатъчна, за да се гарантира безвъзвратното пресичане на нестабилната област.

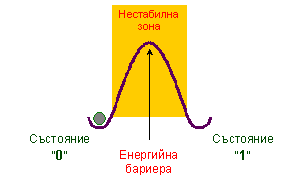
Фиг. 3.1.1.1. Илюстрация на явлението метастабилност

Състоянията “0“ и “1“ в би-стабилната верига се поддържат лесно след като бъдат постигнати. За промяна на едно стабилно състояние в друго е необходим входен управляващ сигнал, който трябва да достави определено минимално количество енергия, необходимо за преодоляване при прехода на нестабилното състояние. Ако входният сигнал доставя повече от минимално необходимата енергия, тогава преходът става много бързо. Ако управляващият сигнал доставя по-малко от минимално необходимата енергия, тогава веригата се връща в първоначалното си стабилно състояние. Съществува вероятност входът да доставя енергия, която е достатъчна за да започне преход, но не достатъчно, за да го принуди да премине бързо през нестабилната област. Тогава веригата може временно да “заседне“ в нестабилната област. Схемите с паметливост се проектират така, че да сведат до минимум тази възможност и да намалят времето, през което веригата е възможно да остане в нестабилно състояние. Ако една схема се задържи в нестабилно състояние твърде дълго, изходът ѝ може да се колебае или да остане по средата между „0“ и „1“, като по този начин кара цифровата система да изпитва непреднамерено и често непредсказуемо поведение. Схема с паметливост, която се застоява в нестабилната област, се определя като метастабилна.

За постигане на статична верига с паметливост е необходима обратна връзка, а всяка верига с обратна връзка притежава свойството паметливост. Всяка логическа схема може да има обратна връзка, ако изходният сигнал е просто "подаден обратно“ и свързан към отделен вход. Повечето схеми с обратна връзка нямат полезно поведение - те или са моно-стабилни (т.е. заседнали в състояние на изход „1“ или „0“), или се колебаят (превключват, осцилират) непрекъснато. Някои вериги с обратна връзка ще бъдат би-стабилни и контролируеми и тези схеми са кандидати за прости схеми с паметливост. Простите схеми с обратна връзка са показани по-долу на следващата фигура и са обозначени като управляеми/не управляеми и би-стабилни/не би-стабилни.

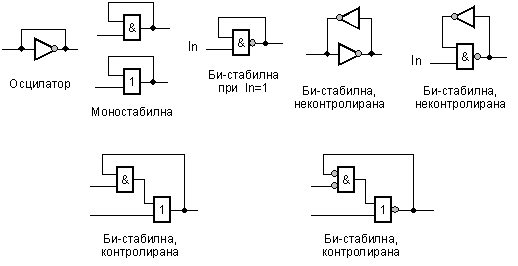
Фиг. 3.1.1.2. Елементарни логически схеми с обратна връзка

Схемите от долния ред в горната рисунка са едновременно би-стабилни и управляеми. Всяка една от тях може да се използва в качеството си на елемент с памет.

Елементарни клетки

И двете вериги, споменати по-горе, използват два входа, наречени S (за установяване - Set) и R (за възстановяване или още нулиране - Reset). Изходът и на двете схеми обикновено се означава с буква Q. Подаване на логическа единица на вход S (S=1, R=0) следва да доведе до изходна единица (Q=1). Аналогичният сигнал по вход R (S=0, R=1) причинява нулиране на изхода (Q=0).

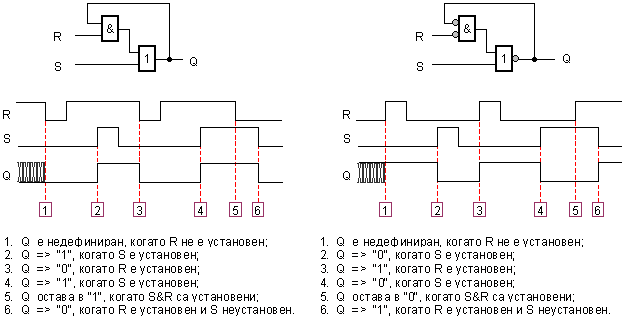
Фиг. 3.1.1.3. Схеми NOR и NAND

В лявата схема И/ИЛИ от горната фигура, сигналът S трябва да бъде повдигнат до “1”, за да промени изходния сигнал Q до стойност "1", след което ниското ниво на входния сигнал R може да възстанови нулевото ниво на изхода Q. С други думи входният сигнал S активно въздейства на схемата с високо ниво, докато сигналът R въздейства с ниско ниво. Паметливостта на тази схема се изразява в това, че изходът Q се задава от положителния входен импулс на S в момент 2, при което изходът Q остава установен и след снемане на входния сигнал S до ниско ниво. Аналогично появата на активната нулева стойност по вход R в момент 3 причинява нулирането на изходния сигнал Q.

Аналогично поведение има и дясната логическа схема, което читателят може да проследи върху приложената времедиаграма. Разликата тук е в това, че въздействията на входните сигнали на изходната стойност се причинява в разменен смисъл.

Веригите NAND и NOR са симетрични, така че всеки вход може да бъде обозначен като S или R. По конвенция изходът Q, който S управлява до “1“, се нарича "прав", а изходът, който S управлява до “0“, се нарича "обратен или инверсен" (notQ). В този смисъл, както вече отбелязахме, дясната схема от горната фигура е обозначена неправилно. Читателят следва да обърне специално внимание и на факта, че в схемата с елемент NOR активните входни стойности са високите (единиците), докато в схемата с елемент NAND, активните нива на входните сигнали са ниските (нулевите).

На следващата фигура 3.1.1.4 по-долу основните клетки са изобразени с кръстосано свързани връзки, като тази на обратната връзка е подчертана. В основната NOR-клетка, изходът Q се извлича от елемента, контролиран директно от вход R, при което R може да определи изхода Q независимо от S - ако R е повдигнат до “1“, то Q ще бъде “0“ независимо от S. По този начин може да се твърди, че базовата NOR-клетка е “reset-доминантнa“. В основната NAND-клетка входът S може да определи изхода Q, независимо от подаденото на R - ако S е снет “0“, изходът Q ще бъде “1“, независимо от R. Така базовата NAND-клетка може да се определи като “set-доминантна“.

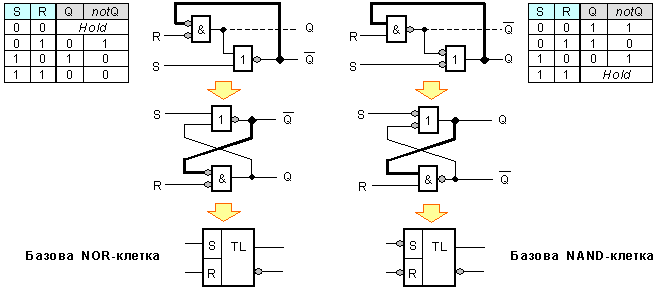
Фиг. 3.1.1.4. Кръстосано свързана верига за обратна връзка.

Разглеждането на горната фигура ни навежда към следните заключения:

· Средните два реда в таблиците на истинност за двете схеми са сходни (т.е. и Q, и notQ се превключват противоположно един от друг, когато е стабилен един от входовете S, или R);

· Когато и двата входа са потвърдени, Q и notQ се управляват до едно и също логическо ниво (т.е. те вече не са инверсни един към друг);

· Когато нито един вход не е потвърден, логическото ниво, присъстващо в контура за обратна връзка, определя изхода на веригата.

Въз основа на тези наблюдения можем да заявим следните поведенчески правила на основна клетка (помнейки, че SET и RESET са активни при високо ниво на сигнала за NOR-схемата и при ниско ниво за NAND-схемата):

· Когато е активиран само вход SET, изход Q се превключва в състояние "1”, а notQ в състояние “0” ;

· Когато е активиран само вход RESET, изход Q се превключва в състояние “0”, а и notQ в състояние “1" ;

· Когато и SET и RESET са активни, Q и QN се превключват в “0” (NOR-клетка) или “1” (NAND-клетка);

· Когато нито SET, нито RESET са активни, изходът се определя от логическата стойност подавана по веригата на обратната връзка.

Ако и двата входа към клетката бъдат деактивирани точно по едно и също време, цикълът за обратна връзка може да стане нестабилен и схемата може временно да се “забие” в нестабилната област. Това е резултат от факта, че две различни логически нива се въвеждат в цикъла за обратна връзка едновременно и тези стойности се “преследват“ един друг в контура, създавайки трептене. Показаното в симулатора трептене е резултат от факта, че закъсненията на логическия елемент могат да бъдат зададени на точно същата стойност, а входовете могат да се променят точно по едно и също време. В реална верига закъсненията не са идентични и входните стойности не могат да се променят точно по едно и също време. По този начин могат да се видят трептения, но само за кратко. Също толкова вероятно е изход, който “плува“ временно между “1“ и “0“. И двете поведения представляват метастабилност, където изходът от схемата временно не е в едно от двете стабилни работни състояния. Метастабилните състояния са малко вероятни в реална верига и ако евентуално се появят, те бързо се прекратяват до стабилно състояние. Но е важно да се отбележи, че възможността схемата с паметливост да влезе в метастабилно състояние никога не може да бъде елиминирано. За това е виновна обратната връзка.

Основните NAND или NOR-клетки могат да се използва в различни практически схеми на памет. В следващото изложение ще използваме NAND-клетка, но подобни схеми могат да бъдат изградени с клетката NOR.

Тригер D-Latch (DL)

Разгледаните основни запомнящи клетки са най-елементарните схеми с памет и са много полезни в определени ситуации. Чрез добавяне само на два логически входа към основната клетка, може да се създаде много по-полезна схема с памет, наречена D-тригер. D-тригерът използва основна клетка за елемент памет, но позволява да се променя съхранената в него стойност (или “да се програмира“). Това може да стане, само когато е потвърден входът C (Control), който управлява момента за промяна. По този начин D-тригерът има два входа: вход C за управление на времето и вход за данни D. Входът за управление на времето, обикновено е наричан “Clock”, “Control” или “Latch enable”, се използва за координиране на момента, когато новите данни могат да бъдат записани в тригера, и обратно, когато данните не могат да бъдат записани. Тригери с управляващ вход С се наричат още "синхронни".

Фиг. 3.1.1.5. D-Latch тригер с NAND-клетка (синхронен) и УГО

Логиката на този процес е илюстрирана по-долу на фигура 3.1.1.6.

Фиг. 3.1.1.6. Времедиаграма за превключване на D-Latch тригер

Читателят следва да обърне внимание на логическата схема от фигура 3.1.1.5, според която стационарната “1" по вход С държи входните NAND елементи “отворени", което означава, че стойността по входа D свободно може да контролира, т.е. да променя, изходната стойност Q. С това се компрометира разбирането, че вход С е входът, който управлява записа на нови данни.

Всички полезни схеми с памет имат поне два входа - един за данновия сигнал, носещ входните стойности, които тригерът трябва да се запаметява, и втори сигнал за управление на времето (на момента) за запис. На фигура 3.1.1.7 е показано разбирането за информацията във времето.

Фиг. 3.1.1.7. Разбиране за данните във времето на входа и на изхода на тригера

Както специално отбелязахме по-горе, в D-тригера настоящото (текущото) състояние и следващото състояние са едни и същи, стига входът за управление на времето С да е установен в “1”. Следва да подчертаем, че полезното управление на тригера, което вход С може да осъществи, е онова управление, при което D-тригерът променя състоянието си в момент на поява на фронт на синхронизиращия сигнал С. Именно появата на този фронт изразява нашето желание (нашата заповед) за запис на нова стойност в тригера. Въпросът за кой фронт става дума (преден или заден) определя конструкцията на логическата схема на тригера, т.е. това зависи от Конструктора.

D-Flip-Flop Тригер (DFF)

D-тригерът, означаван като DFF, за разлика от тригер DL, следва да се разбира като тригер, “работещ по фронт". Разработен е най-вече с цел отстраняване на недостатъка на DL тригера. Той е един от фундаменталните елементи с памет. DFF обикновено има три входа: вход за данни D, който определя следващото състояние; вход С за управление на времето, който задава момента на запис на входната стойност; и приоритетен вход R за нулиране (установяване в нулево състояние).

Управляващият сигнал С е правоъгълен единичен импулс и въпреки, че най-често бива наричан “Clock". Той не е периодичен тактов сигнал, а следва да се разбира като управляващ сигнал, издаван в необходим момент, свързан с алгоритъма за управление на цифровата структура. Записът на нови данни, по чиято заповед се извършва в тригера (регистъра), става в момента на фронта на С импулса. Според логическата схема това може да бъде както предния фронт (RET) така и задния фронт (FET). Такива тригери се наричат “с динамично управление”, "синхронни" и още “работещи по фронт”. Тяхното условно графично означение е следното.

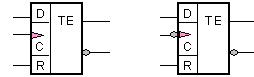
Фиг. 3.1.1.8. Условно графично означение на D-тригер (структура Edge)

Временната диаграма на фигура 3.1.1.9 по-долу илюстрира превключването на RET DFF. Обърнете внимание, че изходът Q се променя само по време на активния фронт на сигнала С. Сигнал по вход R за нулиране принуждава изхода Q да се установи в състояние "0" независимо от другите входове.

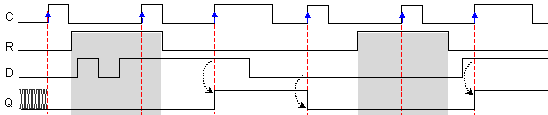
Фиг. 3.1.1.9. Времедиаграма за превключване на D-Edge тригер

Както при основните клетки, тригерите D-Latch или D-Edge могат да влязат в метастабилно състояние, ако данновите и управляващите сигнали се променят точно по едно и също време. Ето защо всеки проектант следва да обезпечава стабилност и надеждност според техническите изисквания, които производителят предписва за своето изделие. Latch тригерите, за които се казва че работят по ниво, данните трябва да са стабилни, докато управляващият вход не отпадне. Edge тригерите, за които се казва че работят по фронт, данните трябва да са стабилни както преди активния фронт, така и известно време след него. Ако данните не са стабилни по време на активния фронт, метастабилно състояние може да бъде синхронизирано в тригера. Ако това се случи, тригерът може да не успее незабавно да разреши ниско или високо ниво да установи на изход. Времето за настройка и задържане на данните варира между няколко десетки пикосекунди (за дизайни в единични интегрални схеми) до няколко наносекунди (за дизайни, използващи дискретни логически чипове).

Логическата схема на основен D-Edge тригер е показана по-долу на фигурата. Различните производители са свободни да предлагат логически схеми, в които има малко различия, но цялостната им функционалност следва да бъде една и съща.

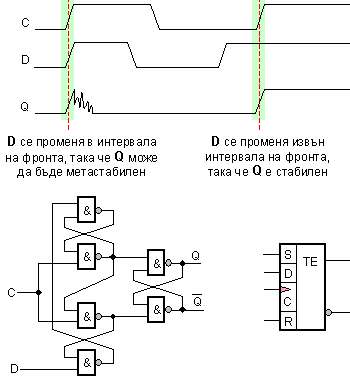
Фиг. 3.1.1.10. Фундаментална логическа схема на D-Edge тригер и УГО

В логическата схема на различните тригери могат да бъдат предлагани различни сигнали за нулиране или за установяване, които обикновено са приоритетни.

В допълнение към нулирането и установъчните сигнали R и S, в схемите на тригерите често се включват още два сигнала. Първият, наречен Clock_Enable (CE), може да се използва, за да се направи тригера отзивчив или неотзивчив към управляващия сигнал C. В много приложения е удобно временно да деактивирате тригера. Изкушаващо е да направите това, като пропуснете сигнала С през елемент И заедно с разрешаващия сигнал СЕ, както е показано по-долу на фигурата. По много причини това е лоша техника на проектиране, която трябва да се избягва, особено при проектиране с FPGA (всъщност много съвременни CAD инструменти не позволяват логическите изходи да управляват синхронните входове). Въпреки че повечето от причините да не се “разрешава управляващия вход” са извън обхвата на това изложение, една от причините е, че изходът елемента И може да се обърка, което да доведе до “изтичане” на нежелани импулси към тригера. Входът CE е специално проектиран да забрани управлението, като същевременно избягва възможни проблеми.

Друга често срещана функционалност се изразява в необходимостта за синхронно нулиране на тригера.

Фиг. 3.1.1.11. Възможни схеми за контрол над управляващия вход

Други Flip-Flop Тригери

Тригерите със структура D-Edge са най-често използваните запаметяващи елементи. Най-същественото им достойнство е, че имат само един даннов вход. В случай че данните са парафазни могат да се използват тригери с парафазни входове като например RS-Edge тригери.

Съществуват тригери и с по-сложна функционалност, като например така наречените JK-Edge или T-Edge тригери. Първият тригер се определя като “универсален”, тъй като чрез различни опроводявания на входовете J и K, могат да се постигат функционалностите на останалите видове тригери. Т-тригерът е единственият тригер, който освен паметливост има още една функция, която се изразява най-ясно чрез логическото ѝ уравнение:

С други думи, новата стойност на изхода Q е сума по модул 2 от текущата му стойност и стойността, подавана по входа Т. Изчислението се извършва по време на записа на новите данни в схемата на тригера. На следващата фигура е илюстрирано превключването на споменатите по-горе тригери.

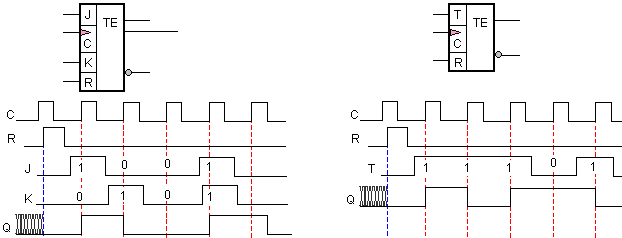
Фиг. 3.1.1.12. Времедиаграми за превключване на JK-тригер и на T-тригер и УГО

Тези тригери обикновено се използват в по-стари цифрови системи (особено в тези, изградени от дискретни логически интегрални схеми, като например тези от серията SN74xxx), но рядко се срещат в съвременния дизайн. Както JK-FF тригер, така и T-FF тригер могат лесно да бъдат конструирани от D-FF тригер, или от първични основни клетки. В съвременния цифров дизайн, и по-специално в проекти, предназначени за FPGA или други сложни логически чипове, тези тригери от последните видове не предлагат никакви предимства и рядко се използват.

Следващият раздел е:

3.2 Логически възли