Последната актуализация на този раздел е от 2019 година.

4. ПРОЕКТИРАНЕ НА УСТРОЙСТВО ЗА СКАЛАРНО УМНОЖЕНИЕ НА ДВА ВЕКТОРА

Поставяме си задачата да проектираме специализирано устройство за изчисление на скаларното произведение S на два вектора x и y:

(x, y)=S (4.1)

Както е известно, скаларното произведение на два вектора по определение е числото:

От гледна точка на математиката, задачата е известна и изчислението на решението се постига чрез формула (4.2).

Тук обаче нашата цел не е самото число S, а техническото средство за получаване на всяко подобно число S. Ето защо ще следваме системната последователност за неговото проектиране, която беше изложена в пункт 1.

Етап А) Изясняване на проблема

Нашите действия, според същността на този етап, са крайно ограничени и улеснени, като се има предвид математическата яснота на поставената задача. Единственото, което читателят може би следва на направи, е да си припомни понятията вектор, скаларно произведение на два вектора, геометрична и алгебрична същност на скаларното произведение, значение и място на тази задача, както и други въпроси, отнасящи се за произхода и областта на приложение на скаларното произведение.

Етап Б) Анализ на поставената задача

Ако трябва да се изчисли числото S, то е необходимо да се знаят стойностите на елементите на двата вектора:

където с m е означен броят на елементите.

Според формула (4.2) и двата вектора имат еднакъв брой елементи. Елементите могат да бъдат числа със знак. Ако имаме предвид произволни стойности, тези числа следва да бъдат представени във форма с плаваща запетая, от където и изчисленията да се проведат в устройство, съобразено с алгоритмите за обработка на такива числа.

Тъй като ние считаме, че формата с плаваща запетая ще усложни ненужно проектирането, което искаме да илюстриране чрез този пример, ще приемем без загуба на общност, че елементите на векторите са цели числа, представени в допълнителен код. На този етап дължината на разрядната мрежа, в която ще бъдат представяни те, ще приемем равна на n[b]. Изчисляването на скаларното произведение S, според формула (4.2), ще протича като повтарящи се операции умножение и натрупващо събиране, което ни води към циклически алгоритъм от вида с предварително известен брой повторения – m. В бъдещото устройство този параметър не може да бъде произволно голям и ще трябва да го ограничим отгоре, т.е. ще приемем за известно някакво максимално число m_max.

Ако приемем, че елементите на двата вектора са даденост вътре в устройството, то те ще бъдат разположени като масиви в две запомнящи устройства с обем от по m клетки всяко. Ако запомнящите устройства за масивите x, y са факт, това означава, че техният обем определя максималната стойност на параметъра m (m_max). От тук следва, че всяка двойка вектори с по-малко на брой елементи също ще може да бъде умножавана скаларно в това устройство, за което ще бъде необходимо да се знае предварително конкретната стойност на m.

Всяка отделна операция умножение на два поредни елемента

ще води до получаване на произведение

което е число с двойна дължина – 2.n[b]. Всяко такова произведение ще се натрупва към междинната сума

която в крайна сметка ще се формира като стойност на скаларното произведение. Събиранията ще бъдат m на брой и ще се извършват върху числа с двойна дължина. Всяко събиране може да удължи междинната сума в старшата й част по причина на възможния пренос, както е показано схематично на фигура 4.1.

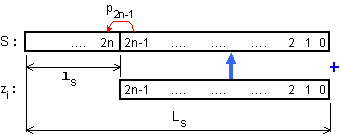
Фиг. 4.1. Схема на вероятното удължаване на междинната сума S

От фигурата се вижда, че старшата част на междинната сума се формира от натрупващият се в нея единствено възможен пренос от (2n-1)-я разряд. Както вече споменахме, събиранията са m на брой, така че необходимата дължина l_s на старшата част на окончателното произведение ще се определи по следния начин:

а общата дължина на полето на резултата ще бъде сумата:

Скаларното произведение ще бъде цяло число, представено в допълнителен код, в поле с дължина L_s.

Всеки път, когато дължината m на векторите x, y , които реално ще се умножават в бъдещото устройство, е по-малка или равна на , ще се получава резултат, който е представим в L_s -разрядното изходно поле, в допълнителен код. Така за резултата от изчислението в устройството признакът препълване няма да бъде възможен.

И на края, последното съображение, което може да бъде изказано на този етап, е конструктивно и се отнася до дължината на полетата, в които ще се представят стойностите на променливите

Ако се приеме, че елементите на векторите са с единична дължина от n[b], то входната шина, през която ще се зареждат в устройството, ще бъде със същата ширина. Тъй като тази шина ще бъде и изходна за устройството, то скаларното произведение като резултат, който е с по-голяма дължина, ще се прочита на части. Тези части ще бъдат три. В тази връзка при една практическа реализация, с цел постигане на простота и ефективност, може да се определи конкретна стойност за параметъра n, която да бъде кратна на дължината на адресируемата единица, източник и приемник на данните. След това с тази дължина следва да се съобразят параметрите m_max и L_s, както и алгоритмите за зареждане на устройството с данни и изчитане на резултата от изходния регистър на същото. Ако адресируемата единица (т.е. входната шина) например има по-малка дължина, нанасяща се няколко пъти в n-битовата разрядна мрежа на числата, то същите ще се записват в паметта на нашето устройство на части, в няколко последователни такта, постъпвайки по входната шина с малка ширина.

Етап В) Синтез на решението

От изложения анализ и изказаните съображения читателят вероятно е вече с изяснено разбиране относно решението на поставената задача. Решението, както беше пояснено в пункт 1, е алгоритмичната схема на изявените в подробности действия. На този етап тази схема е предварителна и формално може да се изложи по следния начин:

1. Инициализация на началните условия:

- нулиране на началната сума S:=0;

- нулиране на индексната променлива i:=0.

2. Последователно зареждане на елементите на първия вектор, i:=i+1.

3. Нулиране на индексната променлива, i:=0.

4. Последователно зареждане на елементите на втория вектор, i:=i+1.

Крайната стойност, която остава в индексната променлива, е m, i=m.

5. Получаване на произведението:

6. Натрупване в междинната сума: .

7. Изменение на индексната променлива: i:=i-1.

8. Проверка на условието за край на цикъла: i=0?:

- ако то не е изпълнено, следва изпълнение на точка 5;

- ако то е изпълнено, следва изпълнение на точка 9.

9. Край, вдигане на флаг “Готов”.

Етап Г) Реализация на решението

Описаната схема е все още обща. Например, сега е моментът да поясним, че устройството което проектираме, ще възприемаме като работещо в състава и по инициатива на външната за него среда. Тази позиция ще ни позволи да определим:

· Входовете и изходите в логическата структура на устройството;

· Алгоритъма на собствената функция и задачите на външната среда.

Още сега ще декларираме, че устройството ще бъде проектирано според изискванията на синхронния метод за управление.

Имайки предвид представената вече последователност, казаното току що се отнася най-вече за инициализацията, зареждането с данни и прочитането на готовия резултат. Устройството ще функционира както самостоятелно, така и под управление на външната среда, което означава, че ролите следва да бъдат разпределени и диалозите уточнени.

Можем да приемем, че проектираното устройство ще бъде неинициативно. Това означава, че в изходно състояние устройството се самоопределя чрез признак (Flag) за готовност, в смисъла на “Готово” или “Заето”, т.е. неготово в смисъла на следната негова кодировка:

Изходното състояние, когато Flag=1, трябва да се постига в два случая:

- принудително, чрез външен сигнал от тип Reset, който ще се подава на специален вход;

- естествено, след изчисляване на всеки пореден резултат.

В изходно състояние ще считаме, че изходният регистър на устройството съдържа резултата и той може да бъде прочетен. В същото време в паметта на устройството продължават да се съхраняват елементите на умножените вектори. Тъй като скаларното произведение се натрупва отзад напред, което се разбира от точка 7 на алгоритмичната последователност, крайната стойност на индексната променлива е нула и тя е удобна за следващата операция.

За всяко следващо изчисление съдържанието на изходния регистър и на паметта са без значение. Ако обаче желаем да улесним потребителя в случай, когато той желае да изчисли последователно няколко различни скаларни произведения:

(x, a) = S_a ; (d, y) = S_d ;

(x, b) = S_b ; (e, y) = S_e ;

(x, c) = S_c ; (f, y) = S_f ;

…….… , или ….…… ,

запазвайки като аргумент един от векторите неизменен, то зареждането на паметта с данни трябва да се реализира разделно, по един и същи начин за всеки от векторите.

Можем още да приемем, че зареждането на данните в паметта на устройството и прочитането на резултата от изходния регистър, ще бъдат функция на външната среда. За целта, освен входната и изходната шина, устройството ще трябва да притежава входове за външни управляващи сигнали, чрез които ще се манипулират логическите възли в неговата структура, при осъществяване на външните алгоритми, както и изход за признака Flag.

Така при тази постановка външната среда ще трябва да изпълнява върху устройството следните алгоритми:

а) Зареждане на първи операнд;

б) Зареждане на втори операнд;

в) Стартиране на изчислението;

г) Прочитане на резултата.

Бъдещото устройство можем да си представим като “черна кутия”, чиито функция, входове и изходи са вече определени – фигура 4.2.

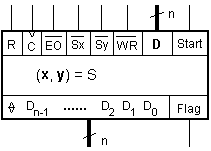
Фиг. 4.2. Функционално означение на устройството

Входната даннова шина е n-разрядна и подава за запис един елемент (едно число) за едно обръщение. Изходната е също n-разрядна, но по нея излиза само една част (порция) от резултата за едно обръщение. Изходната шина е буферирана. Останалите изводи на устройството са следните:

· R Вход за подаване на сигнал Reset. Нормално на този вход ще се подава нула, която е неактивна логическа стойност. При подаване на единица устройството ще минава в изходно състояние, при което трябва да се нулира съдържанието на регистъра на скаларното произведение и на брояча на индекса;

· C Вход на тактовата последователност, която е необходима за тактуване на вътрешното управляващо устройство. Според указателя на входа за сега имаме предвид превключвания по предния фронт на импулсите в тактовия сигнал;

· not(EQ) Вход за разрешаване на изходната даннова шина на устройството. При отсъствие на сигнала шината трябва да е в състояние на висок импеданс. Разрешението на шината е необходимо само при четене на резултата;

· not(Sx ) Вход за избор на запомнящото устройство на вектор х;

· not(Sy) Вход за избор на запомнящото устройство на вектор y;

· not(WR) Вход за стробиращ импулс при запис в запомнящите устройства. Нормалната (дълготрайната) логическа стойност на този вход е единица;

· Start Вход на сигнала за стартиране на изчислението на скаларното произведение;

· Flag Изход - признак за готовност на резултата.

На този етап, когато не сме конкретизирали външната за устройството среда и я приемаме като твърде аморфна и недетерминирана, ще приемем, че тя е в състояние да формира необходимите ни връзки и сигнали. Така, без да се съобразяваме особено с някакви изисквания, ние свободно ще определим нейните алгоритми. След това по-лесно ще се формира алгоритъмът за функциониране на проектираното устройство.

Ще започнем със съвместения алгоритъм “зареждане на първи/втори операнд”:

1. Установява се сигналът

в резултат на което следва да се нулира брояча на индексната променлива i=0.

2. На данновата шина външната среда поставя числото на поредния елемент ( xi , yi ) от съответния вектор (x , y). В рамките на такта, на вход not(WR) се подава стробиращ импулс за запис (not(WR)=0), който фиксира подадения елемент в отворената клетка на избраното запомнящо устройство. С изчезване на нулевия импулс от входа not(WR), следва да се модифицира брояча на индексната променлива i по закона i:=i+1. С това се прави достъпна следващата клетка в запомнящото устройство на съответния вектор (x , y).

3. Проверка за край на зареждането:

- ако все още не са заредени всички елементи на вектора (x , y), следва изпълнение на точка 2;

- ако вече са заредени, следва изпълнение на точка 4.

4. Възстановява се на нормалната стойност на сигнала:

Алгоритъмът “стартиране на изчислението” се състои само от един такт, през времето на който на вход Start, трябва да се подаде активната стойност Start=1. Тази единица следва да се възприеме от вътрешното управляващо устройство, което в отговор трябва да стартира алгоритъма на собствената си функция. В същото време, докато тече изчислението на скаларното произведение, външната среда може да изчаква или да се занимава със себе си.

Последният алгоритъм е “прочитане на резултата”. Той се изпълнява след като се установи готовността на устройството. За целта външната среда трябва да изпълни следното:

1. Проверка на признака за готовност:

- ако устройството е готово (Flag:=1), следва изпълнение на точка 2;

- ако устройството не е готово (Flag:=0), следва изпълнение на точка 1.

2. На вход not(EQ) се подава активна нула (not(EQ)=0), с което се разрешава по принцип четенето на данни от изходния регистър. Тъй като този сигнал е определен от външната среда, можем да приемем, че неговото появяване е синхронизирано с импулсите в тактовата последователност С така че, в края на този първи такт, този сигнал да осигури достъп до младшата порция данни от изходния регистър.

3. В следващия такт, излизащите от устройството данни се фиксират (записват) в клетка на външната среда. В края на такта данновата шина трябва да се превключи към втората порция от изходния регистър.

4. Следва второ по ред записване на данни в нова клетка на външната среда, а в края на такта следва ново вътрешно превключване на данновата шина към третата порция от изходния регистър.

5. В този такт се прочита и фиксира третата порция данни. Тактът е последен и в неговия край изходната шина на устройството трябва да се изключи, като на вход not(EQ) се възстанови неактивната му стойност (not(EQ)=1). При това положение съдържанието на изходния регистър може да бъде четено многократно.

И на края остана да представим алгоритъма на собствената на устройството функция. Според изложеното до момента разбиране, изходното състояние на устройството се представя от признака за готовност (Flag=1), което означава, че в изходния му регистър се намира резултатът, а в паметта – операндите. Ако външната среда междувременно е изпълнила операция “зареждане на операнд”, то съдържанието на паметта на устройството е променено, но то продължава да се намира в изходно състояние. Съдържащият се в изходния регистър резултат обаче вече не съответства на операндите в паметта. Това положение на устройството можем да характеризираме с отделен признак, но на този етап не виждаме необходимост от това. Осигуряването на съответствието между резултат и операнди, както съответствието по дължина между двата операнда, оставяме като грижа и отговорност на външната среда (може да се каже на програмиста). В това състояние индексната променлива i съхранява стойността m, актуална от последното зареждане на операнд.

Вътрешното управляващото устройство поддържа изходното състояние като начално за алгоритъма на скаларното умножение. В това състояние се очаква външната среда да заповяда “стартиране на изчислението”.

Алгоритъмът на собствената функция на устройството вече можем да представим чрез следната последователност:

1. Проверка за стартиране на изчислението (Start=?):

- ако на вход Start е подадена единица (Start=1), следва изпълнение на точка 2;

- ако на вход Start е подадена нула (Start=0), следва изпълнение на точка 1.

2. Нулиране на съдържанието на изходния регистър на устройството (S:=0) и установяване на признака “Заето” (Flag=0).

3. Изпълнява се умножението на двата текущи елемента (zi=xi.yi). За целта текущата стойност на индексната променлива i следва да се интерпретира като адрес и за двете запомнящи устройства x, y едновременно.

4. Полученото произведение се натрупва към междинната сума S:=S+zi.

5. Модифицира се индексната променлива i:=i-1.

6. Проверка на условието за край на изчислението (i=0?):

- ако i¹0, следва изпълнение на точка 3;

- ако i=0, следва изпълнение на точка 7.

7. Установява се признак “Готов”, т.е. Flag:=1.

8. Изпълнява се преход към точка 1.

Етап Г1) Синтез на логическата структура

След всичко казано до момента, готовността ни да представим логическата структура на проектираното устройство вече е голяма. Единствената точка от алгоритъма, която се нуждае от допълнително анализиране, е операция умножение на двата векторни елемента. Известно е, че умножението е циклически алгоритъм. За да облекчим управлението на устройството и за да ускорим изчислението на скаларното произведение, вземаме решение да реализираме операция умножение чрез схемен умножител, т.е. ще търсим реализацията й като еднотактна операция. Тъй като операция умножение ще се изпълнява между числа със знак, представени в допълнителен код, схемният умножител ще проектираме според алгоритъма на Бут (вижте книга [1]), реализиран по схемата с неподвижно множимо. Изборът ни се мотивира от хомогенността на този алгоритъм.

На фигура 4.3 е представена логическата структура на устройството за скаларно умножение на два вектора. В нея се съдържат следните възли:

· RAM X - запомнящо устройство за първи операнд – вектор x;

· RAM Y - запомнящо устройство за втори операнд – вектор y;

· Б.Рг. X - буферен регистър на множимото – вектор x;

· Б.Рг. Y - буферен регистър на множителя – вектор y;

· Бр.i - реверсивен брояч на индексната променлива i;

· УМН - схемен умножител;

· АКМ - натрупващ суматор;

· Л.Сх.1 - логическа схема №1, използвана при четене на резултата;

· Л.Сх.2 - логическа схема №2, използвана при зареждане на операнд;

· Т1 - тригер на признака за готовност на резултата;

· Т2 - тригер за управление на RAM-паметите;

· ВУУ - вътрешно управляващо устройство.

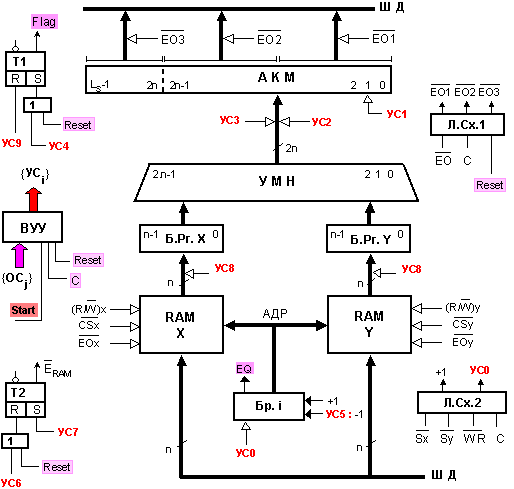
Фиг. 4.3. Логическа структура на устройството

Запомнящите устройства за елементите на двата вектора имат обем от m_max на брой клетки с дължина от n[b]. Така организацията на тези памети се определя като (m_max*n). Ще приемем тези памети за статични, което означава, че те ще имат, както обикновено, три управляващи входа:

· За код на операцията R/not(W) ;

· За избор на паметта not(CS) и ;

· За разрешение на изходните даннови линии not(EQ).

Ако стойността m_max е число, което може да се представи като степенна функция при основа 2, като например числото 256=2⁸, то разрядността на брояча Бр.i се определя лесно (в примера на 8[b]). При такава зависимост броячът е пълноразряден, без излишък и може да бъде определен като кръгов и двоичен. Съдържанието на брояча се дешифрира с цел формиране на признака EQ, (EQ=1 при (Бр.i)=0). При зареждане на данни в паметта на устройството, същата се управлява от логическата схема Л.Сх.2, а при умножение на двата вектора – от тригер Т2 и вътрешното управляващо устройство ВУУ. Изпълнението на функцията на устройството се стартира чрез сигнала Start, който се подава към ВУУ. Към него са подадени още сигналът Reset и множеството оповестяващи сигнали {ОС_j}, а от него излиза множеството на управляващите сигнали {УС_i} .

Буферните регистри Б.Рг. Х и Б.Рг. Y поддържат съмножителите на входа на умножителя, докато паметта се преадресира и станат достъпни следващите съмножители. Самият умножител УМН ще проектираме като комбинационна схема според избрания алгоритъм на Бут.

Акумулаторът АКМ, който натрупва поелементните произведения, ще бъде двутактов.

Логическата схема Л.Сх.1 управлява изходните шини на устройството при четене на резултата от изходния регистър АКМ.

Ще опишем изпълнението на всички операции, отнасящи се до устройството, като само за алгоритъма на собствената функция ще построим микропрограма.

Операция “Зареждане на операнд”

При изпълнение на алгоритмите от тип “зареждане на операнд” се използва логическа схема Л.Сх.2. След стартиране, тези алгоритми установяват на вход not(Sx) или not(Sy), активна логическа нула, при което not(CSx)=0 или not(CSy)=0. На входовете not(EOx) и not(EOy) по това време и на двете RAM-памети се поддържа логическа единица, с което техните изходи са изключени.

Тъй като се предвижда логическата нула на съответния разрешаващ вход not(CS) да е постоянна по време на изпълнение на алгоритъма “зареждане на операнд”, то тя не е удобна за непосредствено нулиране на брояча на индексната променлива Бр.i , защото той ще трябва да се превключва след всеки запис, подготвяйки по този начин следващия адрес в RAM-паметта. Следователно сигналите

ще разглеждаме само като условие за изработване на нулиращия импулс УС0. Този импулс трябва да се издаде от разглежданата схема само веднъж, в началото на алгоритъма.

Втората задача на схемата е да модифицира брояча Бр.i след всеки запис чрез подаване на единичен импулс на входа му “+1”.

Ще приемем, че RAM-паметите работят по принципа на синхронизираната с тактовата последователност операция, без използване на сигнал “готов”. Фиксирането на данните в отворената клетка се осъществява от импулс на активна нула not(WR)=0, който външната среда подава на вход R/not(W) в рамките на всеки такт, когато прави запис. Така алгоритмите “запис на операнд” можем да представим като процес във времето, чрез времедиаграмата от фигура 4.4.

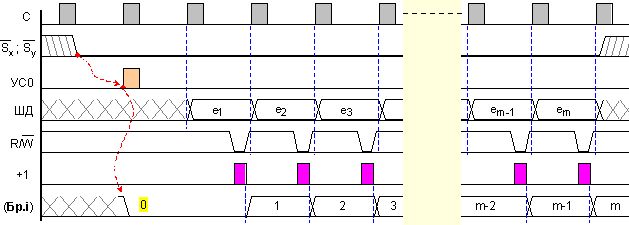
Фиг. 4.4. Времедиаграма на алгоритъм “зареждане на операнд”

Предварително ще обърнем внимание на това, че елементите на векторите, според формула (4.3), се номерират от начална стойност 1, а клетките в RAM-паметите – от адрес 0.

От времедиаграмата се вижда, че подаването на елементите

на зареждания вектор, е съпроводено с подаване на импулс за запис. От всеки такъв импулс се формира импулс “+1” така, че крайното съдържание на Бр.i е числото m. Всяко ново съдържание на Бр.i адресира нова клетка в RAM-паметта и ако последното записване е на елемент №m, и m<m_max, след зареждане на всички елементи, Бр.i ще сочи клетка №m, която е “празна”. Тъй като броячът Бр.i е кръгов (с модул m_max), само в случай, че зарежданите вектори имат дължина равна на максимално възможната m_max, след зареждане на последния елемент, броячът Бр.i ще се нулира, т.е. ще се окаже в своето изходно състояние и ще сочи “пълна” клетка с адрес 0.

Алгоритъм на собствената функция

Както вече беше казано, този алгоритъм е вложен във вътрешното управляващо устройство. В изходно състояние проектираното устройство очаква постъпването на стартиращ единичен импулс на вход Start. Тъй като този импулс се появява асинхронно по отношение на импулсите в тактовата последователност, неговото въздействие ще бъде успешно, ако продължителността му е поне 2 периода на тактовата последователност.

След разпознаване на стартиращия импулс, управляващото устройство започва изпълнението на алгоритъма. В първия такт то издава следните управляващи сигнали:

· УС1 – Сигналът нулира съдържанието на акумулатора АКМ;

· УС6 – Сигналът нулира тригер Т2. От този момент нататък правият изход на този тригер ще поддържа разрешаващия сигнал not(E_RAM)=0, който включва изходните даннови линии на RAM-паметите. Разрешението е едновременно и за двете памети

· УС9 – този сигнал нулира тригер Т1, който ще поддържа от този момент нататък признака “заето”, т.е. Flag=0.

Освен това, за да работят правилно RAM-паметите, на техните входове следва да бъдат осигурени следните постоянни логически стойности:

·

така и двете памети са избрани;

·

така операцията и за двете памети е еднаква.

В следващия такт се подава управляващият сигнал УС5, който модифицира съдържанието на брояча Бр.i с “-1”. В този начален такт, когато след зареждане броячът адресира клетка с №m, която определихме по-горе като “празна” в общия случай, след изваждането на единица броячът подготвя адреса на последно заредената клетка, т.е. (m-1)-та. Това важи включително и за случая, когато m_max.

След адресирането на i-тите клетки, тяхното съдържание е достигнало входовете на буферните регистри Б.Рг.Х и Б.Рг.Y. Така в този следващ такт, чрез УС8, двата елемента (xi и yi), излизащи от RAM-паметите, се записват в тези регистри. Със записването си в регистрите двата елемента встъпват в операция умножение и тяхното произведение следва да се очаква на изхода на умножителя УМН. Произведението ще възникне със закъснение, което е по-голямо от един такт, тъй като умножителят е сложна комбинационна схема. Ето защо се налага в микропрограмата да се включат определен брой празни тактове, преди това произведение да се натрупа в акумулатора. Броят на тези тактове ще определим по-късно.

В следващия такт, когато произведението е вече получено, може да се подаде управляващият сигнал УС2 и да бъде извършено натрупването му към междинната сума, която се съхранява в акумулатора АКМ. Тъй като акумулаторът е двутактов, в следващия такт се подава управляващ сигнал УС3, който разпространява възникналите при събирането преноси.

Така всички микрооперации в цикъла са вече изпълнени и следва проверка на условието за край, т.е. проверява се стойността на признака EQ, който се формира от съдържанието на брояча Бр.i.

В случай, че броячът се е нулирал, това означава, че скаларното произведение е окончателно получено. От това следва, че трябва да се вдигне флагът за готовност като се подаде управляващият сигнал УС4, който установява тригер Т1 в единично състояние (Flag=1). Едновременно с това се подава и управляващият сигнал УС7, който изключва изходните даннови линии на RAM-паметите, като установява тригер Т2 в единично състояние (not(E_RAM)=1).

След този такт, т.е. при следващия тактов импулс, управляващото устройство се връща в изходно състояние, в което очаква следващото стартиране.

Така изказаният алгоритъм на собствената функция е представен на фигура 4.5.

Операция “Прочитане на резултата”

След като външната среда установи готовността на резултата, тя трябва да го прочете. За целта към данновата шина следва да се включат последователно във времето изходните шини на устройството. Те са три, тъй като приехме, че размерът на данновата шина и на елементите на векторите ще бъде еднакъв. Включването на изходните шини се постига чрез сигналите

Формирането на тези сигнали е задача на логическата схема Л.Сх.1. В изходно състояние тази схема трябва да поддържа стойностите

Това състояние на сигналите следва да се осигурява и принудително чрез сигнала Reset.

След подаване на активна логическа нула на вход not(EO), следва да се появи разрешаващият сигнал not(EO)=0. Така младшата порция от скаларното произведение излиза на данновата шина и може да бъде записано в избрана от външната среда клетка. Този запис обикновено се постига от някакъв стробиращ сигнал, чиято активна стойност е нула. Това може да бъде сигналът not(WR), но тъй като този запис е във външната среда, той не ни интересува. В следващите тактове логическата схема Л.Сх.1 се превключва последователно, като генерира и останалите разрешаващи сигнали not(EO2)=0 и not(EO3)=0. След последния такт, когато логическата схема Л.Сх.1 е осигурила достъп до последната порция данни, външната среда прекратява активната логическа стойност на входа not(EO) . От този момент нататък схемата Л.Сх.1 следва да се установи отново в изходно състояние, с което операцията ще завърши.

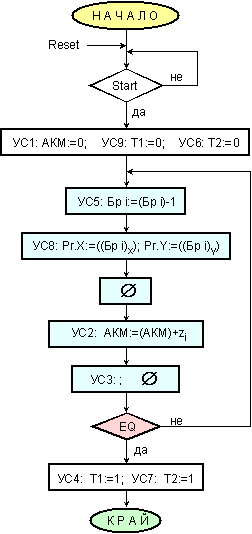
Фиг. 4.5. Блок-схема на собствения алгоритъм

Процесът на четене може да се представи във времето, подобно на процеса зареждане на операнд. Времедиаграмата на този алгоритъм е представена на фигура 4.6.

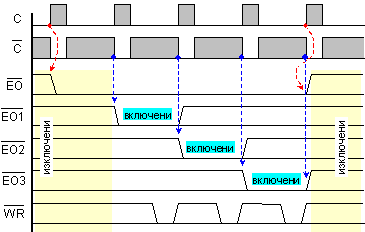
Фиг. 4.6. Времедиаграма на алгоритъм “прочитане на резултата”

Следващият раздел е:

4. Продължение 1