Последната
актуализация
на този
раздел е от 2019
година.
5.
ПРОЕКТИРАНЕ НА УСТРОЙСТВО ЗА ДЕЛЕНИЕ
5.1 Метод за деление
За
реализиране
на операция
деление тук е
избран
методът на реципрочната
стойност.
Според този
метод
частното се
получава чрез
умножение на
делимото с
реципрочната
стойност на
делителя, т.е.
Z=X.(1/Y), където
отношението
1/Y се нарича
реципрочна
стойност на
делителя.
Този метод е
избран от нас
не защото той
е често
използван, а
защото е
много подходящ
в качеството
си на илюстрация
на
структурното
логическо
проектиране,
което тук е
нашата
истинска
задача.
Етап А) Изясняване на проблема
Считаме,
че операция
деление е
изучена от
читателя и
тук няма да
бъде
специално пояснявана.
Ще припомним
само, че тя е
недефинирана
при Y=0. Тук
имаме за цел
проектиране
на устройство
за нейното
изпълнение
по
споменатия
по-горе
метод.
Етап
Б)
Анализ на
поставената
задача
Ако
реципрочната
стойност на
делителя е:
![]()
то
частното Z се
получава
след
умножението X.R=Z.
Ако
приемем, че
операция
умножение не
представлява
проблем на
този етап,
още повече, че
тя беше
разглеждана
в предидущия
раздел 4, на
преден план
излиза
изчислението
на R.
Тъй
като
операция
деление не е
точна операция,
за резултат
се приема
някакво
число Ak , като
негово първо
приближение.
Относителната
погрешност
на този
резултат се
изразява
както следва:
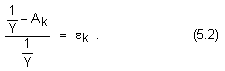
От
получения
израз се
изразява
търсения точен
резултат:
![]()
За
относителната
погрешност ek е
известно, че
е число
по-малко от
единица,
което позволява
отношението,
в което тя
участва, да
бъде
изразено
чрез
разложението
си в безкраен
степенен ред:
![]()
След
заместване в
(5.3), за
реципрочната
стойност се
получава следното:
![]()
Тъй
като не е
възможно да
се работи с
елементите
на един
безкраен ред,
той се
ограничава,
при което
лявата част
на горното
равенство не
е точна и се
замества с
поредното
приближение:
![]()
За
да се намали
броят на
неизвестните
величини в (5.6),
се търси
заместител
на относителната
погрешност ek.
От (5.3) за нея се
получава:
![]()
След
заместване
на ek в
израза (5.6), се
получава:
![]()
Полученото
равенство (5.8)
представлява
рекурентна
формула за
изчисление
на поредното
приближение Ak+1 с
помощта на
предидущото Ak в един итерационен
процес,
чиято
сходимост е
гарантирана
от сходимостта
на
разложението
в степенен
ред (5.4).
За да
се осъществи
итерационният
процес трябва
да бъдат решени
две задачи:
1.
Да се избере
начално
приближение A0 ;
2. Да се
формулира
условие за
край на итерационното
изчисление.
Първа задача
Тъй
като
условието за
сходимост (e<1) трябва
да бъде
изпълнено на
всяка
итерация и
тъй като
оценката за e е известна
от (5.7), то може
да се запише,
че:
![]()
От
така
записаното
отношение
могат да се определят
границите на
интервала на
всяко приближение:
![]()
С
други думи:
![]()
което
се отнася и
за k=0, т.е.:
![]()
При
условие, че
делителят Y е ляво
нормализирано
число в една n-битова
разрядна
мрежа (виж
подробностите
в книга [1]),
то като такъв
,той
удовлетворява
следното
неравенство:
![]()
![]()
Тогава
неравенството
(5.11) може да се
преопредели
както следва:
![]()
И
така, на ляво
нормализиран
делител от
вида Y=(0
1yy…yyy) в n-битова
разрядна
мрежа с дясно
фиксирана запетая:

съответства
начално приближение
![]()
което
ще бъде
представено
в разрядна
мрежа с ляво
фиксирана
запетая:
![]()
което
според
неравенство
(5.13) може да бъде
избрано
измежду
следните n-разрядни
стойности:
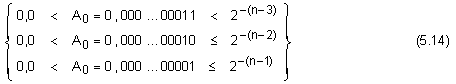
Втора задача
Заедно
с
изчисляването
на
приближенията
![]()
трябва
да се
изчисляват и
съответните
им относителни
погрешности
![]()
които
гарантирано
намаляват и
клонят към нула.
Навярно на
читателя
вече е ясно,
че условието за
край на
цикличното
итерационно
изчисление
на
реципрочната
стойност се
формулира
чрез
относителната
погрешност с
помощта на
следното
неравенство:
![]()
Етап
В)
Синтез на
решението
Необходимите
изчисления,
определени в
избрания
метод, могат
да бъдат
описани чрез
последователността
представена
по-долу,
представляваща
алгоритъма-решение
на
поставената
задача: Като
имаме
предвид
множеството
изложени в книга [1]
алгоритми,
без загуба на
общност тук
ще приемем,
че
операндите
са само положителни
числа. С това
фактически
отстраняваме
проблемите
със знака и
съсредоточаваме
усилията
само върху
същинската
операция.
1.
Приемат се
двата
операнда.
2.
Установява
се
конструктивно
избраната
начална
стойност на
приближенията
A0.
3.
Изчислява
се произведението (Y.Ak).
Полученото
произведение
е необходимо
за изчисление
на
относителната
погрешност ek според (5.7) и
за
изчисление
на израза (2-Y.Ak), според
(5.8). Според (5.9)
полученото
произведение
е число
по-малко от
единица и
изчислението
на посочения
израз не се
извършва
фактически,
тъй като по
определение (книга [1]),
неговата
стойност
представлява
допълнителния
код на
двоичното
число (-Y.Ak).
Относителната
погрешност
също не се
изчислява
фактически,
тъй като тя
представлява
дробната
част на числото
(2-Y.Ak). Така за
следващата
точка на
алгоритъма
се формулира
следното
действие:
4.
Получава се
допълнителният
код на числото
(-Y.Ak).
5.
Проверява
се условието
за край на итерационния
процес
- ek < e ?
- ако
условието е
изпълнено,
следва изпълнение
на точка 7.
- ако
условието не
е изпълнено,
следва изпълнение
на точка 3;
6.
Изчислява
се
следващото
приближение
![]()
При това
изчисление
текущото
приближение Ak - (число
с ЛФЗ) се
умножава с
полученото в
предидущата
точка 4 число.
Въпреки, че
това число е
по-голямо от
единица, то
се приема за
число с ЛФЗ,
като в последния
такт се
умножава и с
цифрата,
стояща в
неговия
знаков бит.
7.
Множимото Х
се умножава с
последно полученото
приближение.
Полученото
произведение
(X.Ak) следва
най-правилно
да се
възприема
като реално
число.
Бихме
могли да
усъвършенстваме
изказания
алгоритъм.
Например в
него не е
заложена нито
проверката
на условието
за дефинираност,
нито
проверката
за
изпълнимост
на операцията.
Интересно би
било и
бързото получаване
на резултат в
случай, че X=Y,
когато Z=1, или в
случай, че Y=1,
когато Z=X,
както и някои
други
интересни
случаи. Това
обаче ние не
сме
направили
умишлено. Усложняването
на
алгоритъма
би ни затруднило
излишно в
постигането
на учебната
ни цел – проектиране
на
логическата
структура
като процес.
В този смисъл
искаме да
предупредим
читателя, че
окончателните
схемни решения,
които ще
бъдат
получени
по-нататък,
не са
достатъчно
перфектни за
директно
практическо
приложение.
На тях
читателят
може да гледа
като на една
много добра
основа за
по-нататъшно
развитие на
устройството.
Следващият
раздел е: