Последната актуализация на този раздел е от 2019 година.

5.2 Примери

Синтезираният алгоритъм следва да се демонстрира на практика, т.е. при изпълнение върху конкретни операнди. Изпълнявайки на ръка операцията по предписаната последователност е изключително полезно, предвид предстоящия синтез на логическата структура на устройството за деление.

ПРИМЕР 1. Да се изпълни операция деление Z=X/Y на числата X=120 и Y=3, които са представени в разрядна мрежа с дължина n=8[b] в прав код.

Този пример се характеризира с това, че частното е точно (Z=40,0) и то се изчислява вярно по методите цифра по цифра. Когато обаче се прилага разглеждания тук метод, реципрочната стойност на делителя Y=3,0 е неточно число, тъй като е периодична дроб: R=0,333333333…=0,(3). Тогава при умножение на делимото X с тази стойност ще се получи частно, което е по-малко от точния резултат, колкото и дълъг да е множителят R. Ето защо при този метод правилно е на частното да се гледа като на реално число, т.е. число с цяла и дробна част. В случай, че частното трябва да се формира като цяло число, то може да се извърши закръгляне.

Тъй като зададената разрядна мрежа е на числа с дясно фиксирана запетая, то според (5.14), началното приближение A₀ ще изберем да бъде стойността: A₀ = 0,0000011.

При това положение за относителната погрешност, която трябва да удовлетворим според (5.15), се получава числото

Първа итерация:

Забележка: Всички операции умножение на делителя Y с текущото приближение A_k в примера тук са изпълнени като за множител е използван делителят Y, т.е. (A_k.Y). Това е направено единствено с цел икономия на място. Изключение прави последното умножение, с което се получава резултатът Z. Последното умножение (X.A_k) читателят може да разглежда като пример за всички умножения, за които става дума в тази забележка, като например следващото по-долу.

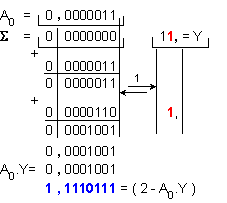
Следва изчисление на приближението A₁ във формат с двойна дължина:

Полученото приближение е с двойна дължина. Относителната погрешност на полученото приближение се изчислява по формулата:

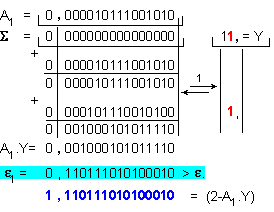
Втора итерация:

Полученото приближение е с четворна дължина, но в следващите изчисления то се фиксира с двойна дължина без закръгляне. Тази загуба на точност може да доведе само до по-бавен процес на схождане.

Относителната погрешност на полученото приближение се изчислява по формулата

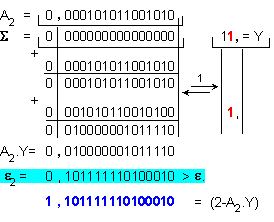
Трета итерация:

Относителната погрешност на полученото приближение се изчислява по формулата

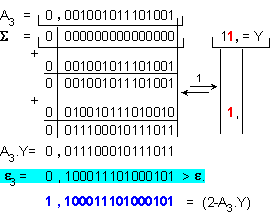
Четвърта итерация:

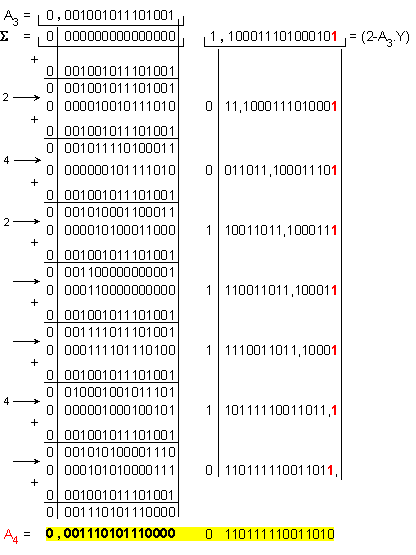
Относителната погрешност на полученото приближение се изчислява по формулата

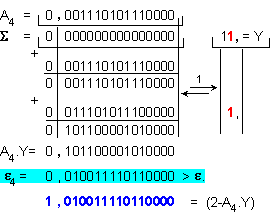
Пета итерация:

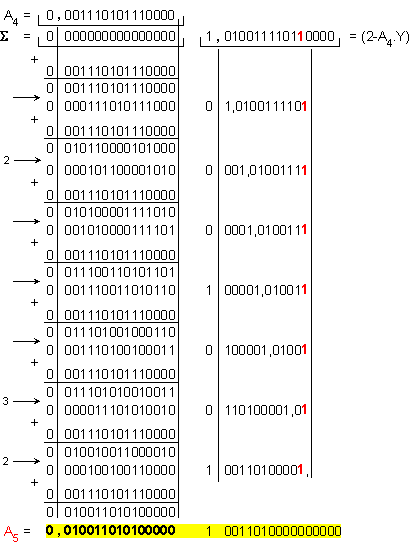
Относителната погрешност на полученото приближение се изчислява по формулата

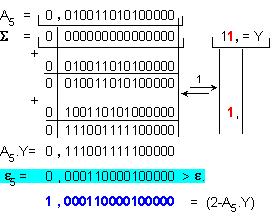
Шеста итерация:

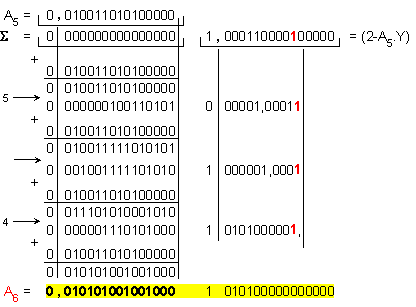
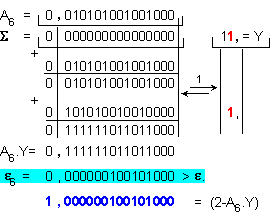
Относителната погрешност на полученото приближение се изчислява по формулата

Седма итерация:

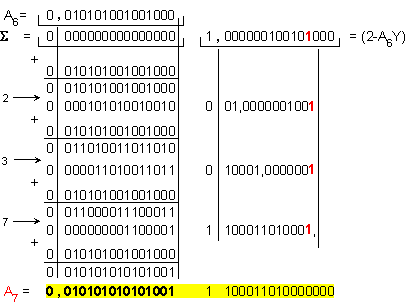
Относителната погрешност на полученото приближение се изчислява по формулата

.

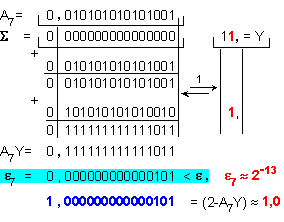
Тъй като след тази итерация относителната погрешност на приближението A₇ става по-малка от допустимата, зададена в началото, то получената стойност 0,010101010101001 се приема за стойност на отношението (5.1). Остава последното умножение, с което се получава частното Z.

Полученото двоично частно е с четворна дължина (двойна дължина за цялата част и двойна дължина за дробната част) и има следния приблизителен десетичен еквивалент:

100111,111111100111 » 39,993896484375 ,

което потвърждава казаното в началото на примера за точността на резултата. Полученото частното е по-малко от точния резултат, тъй като междинните резултати са с фиксиран формат и закръгляне не е правено. Запетаята на реалното число е фиксирана в средата. Ако е необходим резултат с дясно фиксирана запетая с единична дължина, може да се извърши закръгляне, при което ще се получи частно: 101000, = 40, и след това за резултат се вземе само цялата част на числото, която се намира в младшата част на лявата половина.

ПРИМЕР 2. Да се изпълни операция деление Z=X/Y на числата X=68 и Y=5, които са представени в разрядна мрежа с дължина n=8[b] в прав код.

Тъй като зададената разрядна мрежа е за числа с дясно фиксирана запетая, то според (5.14), за начално приближение A₀ ще изберем стойността: A₀ = 0,0000010.

При това положение, за относителната погрешност, която трябва да удовлетворим според (5.15), се получава числото

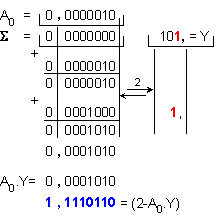
Първа итерация:

Забележка: Всички операции умножение на делителя Y с текущото приближение A_k в примера тук са изпълнени като за множител е използван делителят Y, т.е. (A_k.Y). Това е направено единствено с цел икономия на място. Изключение прави последното умножение, с което се получава резултатът Z. Последното умножение (X.A_k) читателят може да разглежда като пример за всички умножения, за които става дума в тази забележка, като например следващото по-долу.

Следва изчисление на приближението A₁ във формат с двойна дължина:

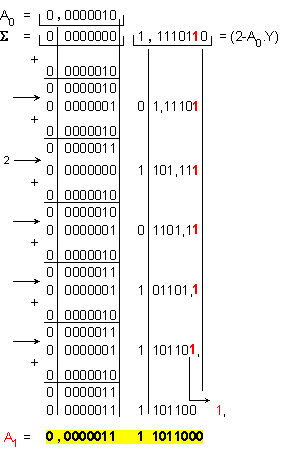
Полученото приближение е с двойна дължина.

Относителната погрешност на полученото приближение се изчислява по формулата

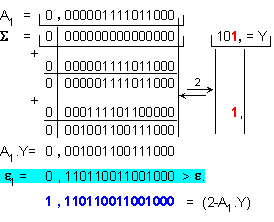
Втора итерация:

Относителната погрешност на полученото приближение се изчислява по формулата

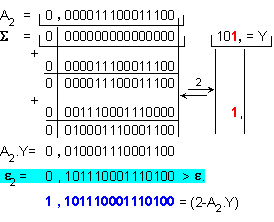
Трета итерация:

Относителната погрешност на полученото приближение се изчислява по формулата

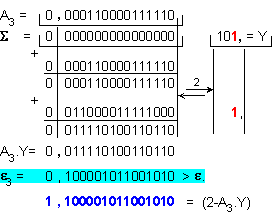
Четвърта итерация:

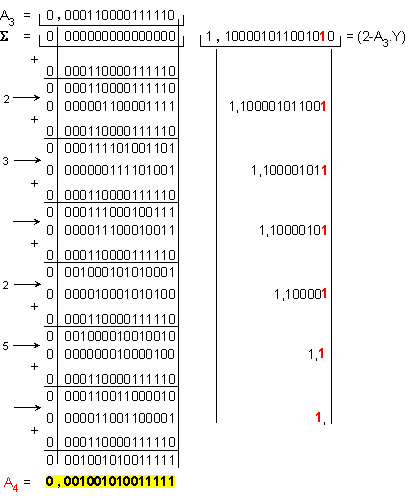
Относителната погрешност на полученото приближение се изчислява по формулата

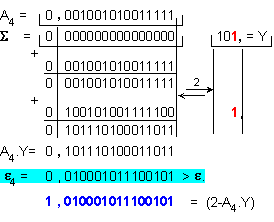
Пета итерация:

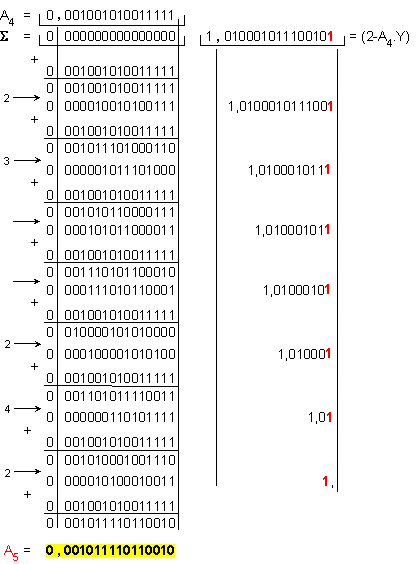
Относителната погрешност на полученото приближение се изчислява по формулата

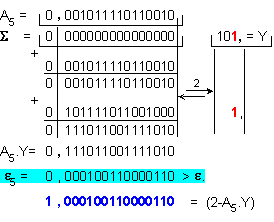
Шеста итерация:

Относителната погрешност на полученото приближение се изчислява по формулата

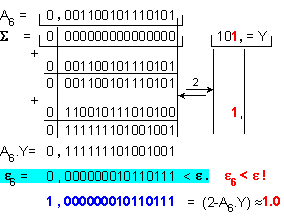
Тъй като след тази итерация относителната погрешност на приближението A₆ става по-малка от допустимата, която е зададена в началото, то получената стойност 0,001100101110101 се приема за стойност на отношението (5.1). Остава да се извърши последното умножение, с което се получава частното Z.

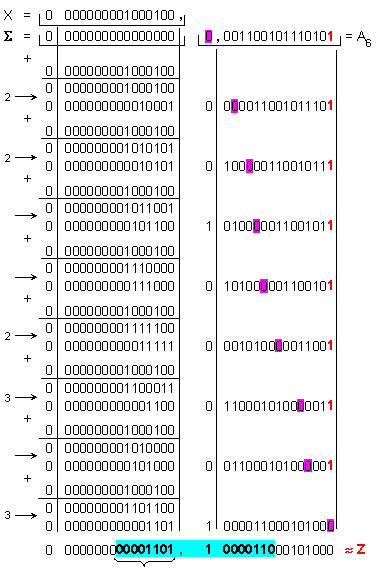
Полученото двоично частно е с четворна дължина и има следния приблизителен десетичен еквивалент:

1101,100001100010100 » 13,5240478515625 .

Точната стойност на частното е 13,6. Запетаята на реалното число е фиксирана в средата. Ако е необходим резултат с дясно фиксирана запетая с единична дължина, може да се остави само цялата част на числото, която се намира в младшата част на лявата половина.

Следващият раздел е:

5.3 Проектиране