I.
КОМБИНАЦИОННИ
СУМАТОРИ
I.1.
Основни
положения
Операция
аритметическо
събиране Z=X+Y се
изразява
чрез
системата
уравнения (1.2.1),
представена
в книга [1].
Операндите X,Y в
тази
двуместна
операция са
числа,
представени
в позиционна
бройна
система.
Операцията
се изпълнява
поразрядно и
последователно,
започвайки
от
най-младшия
разряд в
посока към
най-старшия,
според определението
й в
съответната
бройна
система. Например
за
десетичните
цифри 8 и 7 получаваме:
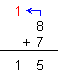
т.е.
двуцифрената
сума 15, където
старшата цифра
1 е получена в
резултат на
възникналия
пренос.
Операция
събиране в
двоична
бройна система
се дефинира с
помощта на
следната
таблица:
Таблица I.1
Аритметическо
събиране на
двоични
цифри
|
x |
y |
z |
p |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
където: x,
y -
аргументи, елементарни
количества
на бройната
система - (двоични
цифри 0,1);
z - функция на
двоичната
сума x+y -
(двоична
цифра);
p -
функция на
двоичния
пренос
- (двоична
цифра).
В
таблицата и в
представения
пример е изразено
следното
общо
определение
за събиране в
позиционна
бройна
система: ако при
събиране на
двете цифри (x+y) се
получи
резултат,
който
представлява
елементарно
количество,
последното
се представя
от
съответната
му цифра, в
противен
случай
резултатът
се намалява с
число, равно
на основата
на бройната
система.
Получената разлика
е
елементарно
количество,
което се
представя от
съответната
му цифра.
Ощетеният в
дадената
позиция
резултат в
този случай
се
компенсира с
помощта на
функцията на
преноса в
следващата
по-старша
позиция.
Основната
ни задача тук
е да построим
такова
техническо
средство,
което би
могло да извършва
описваната
операция
вместо нас. Това
техническо
средство се
нарича полусуматор.
В общият
случай, в
един разряд
се изчислява сумата:
![]()
където
се вижда, че
последователно
следва да се
изпълнят 2
операции
събиране, т.е.
събират се 3
операнда. Тъй
като горната
таблица дефинира
само едно
събиране, т.е.
половината
от необходимите
изчисления,
то
техническото
средство се
нарича
полусуматор.
Техническото
средство
полусуматор
трябва да има
два входа, на
които ще се
подават двата
операнда и
два изхода,
на които ще
излизат
стойностите
на двете
функции.
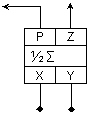
Непосредствена
реализация
на аритметичната
операция
събиране
според
цитираните
уравненията (1.2.1)
от книга [1], в
произволна
позиционна
бройна
система, не е
известна.
Решението
на така
поставената
задача все пак
се постига в
условията на
двоична бройна
система, при
отчитане на
факта, че двоичните
цифри могат
да се
интерпретират
като логически
константи,
а таблицата,
която
дефинира
аритметичната
операция
(таблица 1) - да
се
интерпретира
като таблица
на истинност.
При тези
условия е
възможно
функциите на
сумата и
преноса да се
търсят като логически
функции
чрез
методите на
алгебрата на
логиката. И тъй
като за
реализация
на
логическите
функции са
известни
технически
средства, то
може да се
приеме, че
поставената
задача за построяване
на
техническо
средство, е
решима.
Прилагайки методите на алгебрата на логиката за търсените логически функции се получават следните уравнения:
![]()
Логическата
схема,
реализираща
уравненията
(1), работи
с логически
стойности,
провежда логически
изчисления и
получава за
резултат
логически
стойности, но
за щастие те
напълно
съответстват
на
аритметическите,
интерпретирани
според
таблица 1.
Тук
е необходимо
да обърнем
внимание на
факта, че в
някои не особено
прецизни
литературни
източници, наименованието
полусуматор
се приписва
на схеми,
реализиращи
само първото
от
уравненията
(1), т.е. елементарната
логическа
функция
"неравнозначност",
която се
предлага на
пазара
например в
интегралната
схема 7486 и др.
Това е
некоректно,
тъй като
полусуматорът
се определя
като схема с
два изхода,
реализиращи
съответните
логически
функции на
сумата z и
преноса p,
според
синтезираните
за тях
уравнения (1).
Следващият
раздел е: