Този раздел е добавен в тази книга през март 2023 година.

I.10. Микроконвейерни комбинационни суматори

Обоснование за синтез на конвейерна организация

Често математическите изчисления се нуждаят от стойността на последователни операции събиране, които в общия случай можем да изразим така

, (1)

Такива ситуации се срещат често във векторните и матричните изчисления, в статистическите изчисления, при изчисление на различни оценъчни норми.

Подобни ситуации влияят и на архитектурата на цифровите процесори, стремящи се към осигуряване на все по-висока производителност. Типичен пример са така наречените VLIW-архитектури.

Последователните операции от тип събиране ни навеждат на идеята за една нова организация на изчисленията, при която би било възможно прилагане на непосредствено конвейеризиране. Естествено главната цел, която ще преследваме, е свързана с повишаване на производителността.

В нашите изследвания (книга [1], [2], [3], [5]) могат да се намерят разнообразни методи, разработвани както върху схемата, така и върху структурата на самия суматор, а освен това и върху общата организация на едновременното събиране на много операнди и получаване на структури и схеми, наричани концентратори. Прилагат се разнообразни методи за организация на разпространение на преноса между отделните разряди, който е основният източник на закъсненията. Така се стига до суматори с ускорен последователен пренос, с асинхронен пренос, с групов пренос, с паралелен пренос, с групов паралелен пренос и пр. С увеличаване на броя на едновременно подаваните входни операнди на 3 и повече са разработени и изследвани различни схеми и логически структури, наречени концентратори.

Тъй като операция събиране на две мнигоразрядни числа (a+b) се извършва поразрядно и паралелно във всички разряди по един и същи начин, то синтезът на логическата схема на един многоразряден суматор се свежда до набиране на необходимата дължина за резултата с помощта на схемата на едноразряден двоичен суматор, чиито логически уравнения са следните:

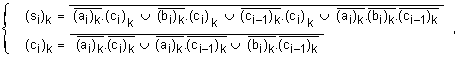(2)

където с буквите s, c са означени значенията на i-тия бит на сумата и преноса при събиране на k-тата двойка операнди.

Така например, за събиране на два 8-разрядни операнда ще трябва да се реализира 8-разряден паралелен суматор от 8 еднакви едноразрядни суматора, които следва да се свържат помежду си така, че възникващите в по-младшите разряди преноси да се разпространяват в посока на по-старшите разряди като аргументи с необходимата логическа стойност. Това включване води до логическата схема на суматор с последователен пренос. Техническите параметри на този суматор, както и на вече споменатите, могат да бъдат намерени в посочените по-горе източници.

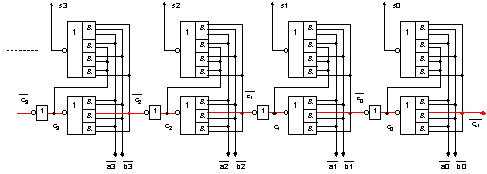
Фиг. I.10.1. Логическа схема на комбинационен суматор с последователен пренос

За да поясним тук нашето изследване, ще обърнем внимание на времето за превключване на логическата схема и процеса на закъснение при разпространение на междуразрядните преноси. Разпространението е последователно от по-младшите разряди към по-старшите, което е обусловено от теорията на позиционните бройни системи. В резултат на това лесно се съобразява, че продължителността на изчисляването на резултата зависи от дължината на суматора, при което обикновено се приема, че закъснението е едно и също във всеки отделен разряд.

И така, възниква главното съображение, че след като формираният пренос в даден i-ти разряд, се разпространи в следващия (i+1)-ви разряд, то текущият едноразряден суматор се оказва свободен. Спрямо горната схема това означава, че след преминаване на преноса c₀ в разряд №1, младшите входове (a₀,b₀,c_-1) се оказват свободни. По индукция това заключение може да бъде разпространено за всеки следващ разряд до пълната дължина на суматора. Въпреки че в началото беше казано, че двойката операнди (a,b)_k се подават едновремено на входа на суматора, във връзка с току що изказаното съображение, възниква идеята, според която към входовете на най-младшия суматор (който е вече свободен) могат да бъдат подадени младшите две цифри на следващата двойка операнди (a₀,b₀)₁. Изхождайки от (1), с това се открива възможност за нова организация на процеса, позволяваща той да бъде ускорен. Тази нова организация изисква конвейеризация на подаването на операндите към входовете на суматора. За нейното реализиране е необходимо да се приложи подходяща синхронизация.

Синтез на конвейерната организация

Първоначално ще приемем да наричаме условно времето за превключване на едноразрядния суматор, т.е. неговото закъснение, такт. Така можем да говорим, че входните цифри на втория едноразряден суматор (a₁,b₁,c₀), са необходими със закъснение на един такт по отношение на вече подадените и употребени такива в по-младшия разряд. Това съждение може да бъде разпространено върху всички следващи по-старши разряди на суматора. В крайна сметка това ни води до следващата примерна логическа структура на 4-разряден суматор.

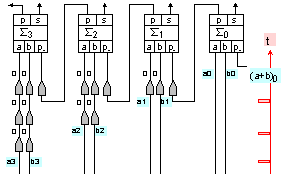
Фиг. I.10.2. Схема на тактовата последователност

На рисунката е изобразена схемата на последователността, в която следва да бъдат подавани цифрите на операндите от първата двойка събираеми (a,b)₀ към 4-разрядния суматор. За да се съвместяват синхронно във времето цифрите от съответния разряд (a_i,b_i) с появата на необходимия пренос (c_i-1), в схемата са въведени задържащи елементи на един такт (τ [s]). Така например се вижда, че двойката цифри (a₃,b₃), която следва да постъпи на четвъртия едноразряден суматор, е задържана във времето на три такта по отношение на двойката в най-младшия разряд (a₀,b₀). По този начин тя ще се съчетае във времето правилно с преноса (c₂), който идва от суматор №2. Във всички разряди на така образуваната тактова схема се подават нули (0,0). На времедиаграмата вдясно са показани синхронизиращите импулси, с които се тактуват отделните нива на входните набори от цифри.

Отчитайки факта, че елементите на тактовите задръжки следва да се използват ефективно при реализиране на изчислението (1), не е трудно да се съобрази, че процесът на последователно подаване на първата двойка събираеми, трябва да се допълни с последователното подаване на следващите двойки събираеми, така щото да няма загуба на време от напразно пробутвани в последователността нули (вижте фиг. I.10.2).

За пълното реализиране на последователното събиране (1), към входовете на суматора са включени регистрите RG0, RG1, RG2 и RG3, в които са заредени съответните двойки събираеми, както е показано на фигура I.10.3.

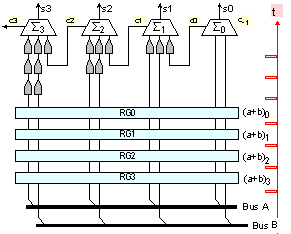
Фиг. I.10.3. Буфер на входните събираеми

Както следва да се очаква, отделните разряди s_i на получаваните суми се явяват на изходите на едноразрядните суматори, последователно във времето, със задръжка на такт спрямо по-младшите s_i-1 . По тази причина, с цел тяхното подравняване, към изходите на суматора е включена аналогична на входната задържаща структура, но огледално обърната, както е показано на фигура I.10.4.

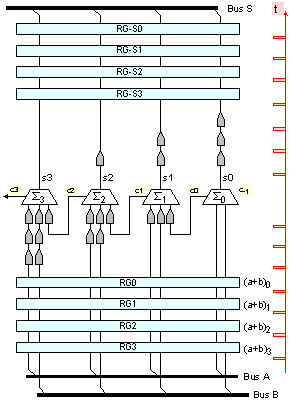
Фиг. I.10.4. Логическа структура на микроконвейера

Оценки на скоростта

Представената 4-разрядна логическа структура може да се определи като конвейер, или още като конвейеризиран комбинационен суматор, получаването на който целяхме от самото начало. Ако по входните шини А и В последователно на всеки такт се зарежда двойка събираеми, то сумата от всяка двойка ще се явява на изходната шина S след 12 такта. Така за получаване сумите на 4 последователни двойки операнди ще са необходими 12+4 такта, или общо 16 такта. В обикновения случай, когато суматорът не е оборудван с конвейерната структура, за същия обем изчисления ще бъде необходимо следното време: ще е необходим един такт за зареждане на входните портове с двойката операнди, след това следва да се изчакат още 4 такта за окончателното разпространение на преносите в суматора, и още един такт за запис на изходния резултат в изходния порт. Така за получаване на сумата от една двойка операнди ще са необходими общо 6 такта. Ако е необходимо да се съберат последователно 4 двойки операнди, както предполага примерната конвейерна структура от фигура 4, то за такова изчисление ще е необходимо 4 пъти повече време, което се определя лесно, и което достига общата стойност от 6.4=24 такта. Така става очевидно преимуществото на конвейерната структура, тъй като 16<24.

В общия случай, за n разряден суматор, който ще събира 4 двойки операнди, оценките ще бъдат следните: 4 входни такта за зареждане на входния регистров буфер + (2n-1) такта от задържащите елементи и суматора + 4 такта за зареждане на изходния регистров буфер, или общо

T = 4τ + (2n-1)τ +4τ = (2n+7)τ [s] . (3)

За алтернативния вариант на структурата, времето за изчисляване се определя така: един такта за зареждане на входните регистрови портове + n такта за получаване на сумата + 1 такт за зареждане на изходния порт, общо (n+2) такта. За събиране на 4 двойки операнди общото време е

T = 4(n+2)τ [s] . (4)

Сравнението показва очевидна полза на оценката (3) пред оценката (4).

В оценките може да бъде вкарана зависимост и от броя на двойките за събиране според (1), но не трудно да се съобрази, че направеният извод няма да се промени и даже ще се засили.

Съображения относно апаратната реализация

Последните пояснения, които ще изложим, се отнасят до апаратната реализация на конвейерната структура. На първо място ще уточним, че задържащите на такт логически елементи следва да се реализират със синхронни Edge D-тригери.

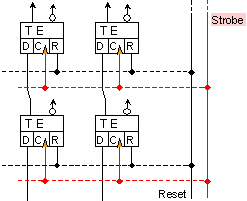
Фиг. I.10.5. Синхронен Latch D-тригер

Тези тригери реализират необходимата задръжка на един такт. Продължителността на задръжка, която представлява периода на тактуващата последователност (период на управляващите импулси Strobe), трябва да се настрои спрямо времето за превключване на едноразрядния комбинационен суматор.

На второ място ще отбележим, че по силата на тази логика, регистрите на входния и на изходния буфери също трябва да се изградят от Edge D-тригери (динамични тригери работещи по фронт). Тези буфери могат да се интерпретират като FIFO-буфери. Предаването на данните по вертикала (вижте фигура I.10.4) става едновременно (паралелно) от регистър в регистър по заповед на управляващия строб импулс (Strobe).

На трето място поставяме твърдението, че 4-разрядната логическа структура от фигура I.10.4 е само примерна и в нея може да бъде употребен комбинационен суматор с:

· Произволна дължина ;

· Произволна структура.

Общият случай ни задължава при синтеза да съобразим структурата на задържащата схема на входа и на изхода на суматора със структурата на самия суматор.

Следващият раздел е:

2. Натрупващи суматори