Последната редакция на тази книга е от 2021 година.

I.2. Пълен едноразряден двоичен комбинационен суматор

Случаят на паралелно събиране на многоразрядни числа, представлява изпълнение на операцията във всеки отделен разряд според определението, по един и същи начин (събиране на съответните две цифри и пристигналият от по-младшия разряд пренос). В този случай суматорът се нарича "многоразряден" или още "паралелен". Повтарящата се във всеки отделен разряд ситуация позволява задачата за синтез на такъв логически възел да бъде сведена до задача за синтез на схема, реализираща операцията в един единствен разряд. Мултиплицирането и подходящото свързване на тази едноразрядна схема ще позволи да се изгради суматор с произволна дължина. Многоразрядният комбинационен суматор като структурен елемент ще означаваме както следва:

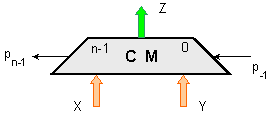
Едноразрядното аритметическо събиране в произволен (i-ти) разряд при описаните условия се представя със следващата таблица I.2.

Таблица I.2 Пълно едноразрядно двоично събиране

0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

По аналогичен начин, интерпретирайки тази таблица като таблица на истинност, функциите на сумата z_i и на преноса p_i могат да се синтезират като логически функции от логическите аргументи:

където с i е означен номерът на текущия разряд.

Прилагайки методите на алгебрата на логиката за аналитично и минимално представяне на логическите функции, от таблицата се получава следната система уравнения:

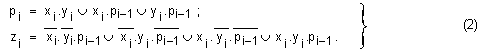
Тъй като не са приведени извършените преобразования, е необходимо да отбележим, че читателят следва да обърне внимание на функцията на сумата, която не се е минимизирала и е останала в съвършенната си нормална форма. Това се вижда много ясно, ако се попълни картата на Карно за 3 аргумента.

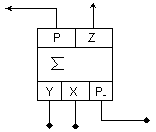
Системата уравнения (2) изразява аналитично пълния едноразряден двоичен комбинационен суматор, чиято техническа реализация се търси във вид на схема, имаща три входа и два изхода, както е показано тук.

Съществуват множество функционално пълни системи логически функции, в които може да се търси практическа реализация на уравненията (2). Изборът се определя най-вече от технологията на производство на електронните схеми. Като типичен пример може да се посочи серията TTL интегрални схеми 74xx, която е пример за тризвенна инверсна логика в базиса И-ИЛИ-НЕ. Тъй като тук се стремим към техническата реализация, то ще търсим израз на получените логически изрази именно в инверсна логика. Читателят следва да познава добре градивните логически елементи, и тук ние разчитаме на това му познание, за да не ни се налага да обесняваме, че инверсната логика осигурява товароспособността на изходите на практическите логически елементи.

Така след подходящи преобразования, за функцията на преноса може да се получи:

Уравнението за функцията на сумата (2), което е останало неминимизирано, т.е в съвършена нормална дизюнктивна форма (СНДФ), не е съвсем подходящо за реализация. Известно опростяване то може да получи, ако функцията на сумата се потърси, като функция и от текущия пренос, т.е.

За целта функцията се представя в картата на Карно за 4 аргумента както следва:

		00	01	11	10
	00	0	*	*	1
.	01	1	*	0	*
	11	*	0	1	*
	10	1	*	0	*

След извършване на оптималните слепвания се получава следния минимален вид за логическата функция на сумата:

а след необходимите преобразования, записът на функцията на сумата в инверсна логика приема вида:

Така полученото уравнение заедно с уравнението на функцията на преноса представлява нов запис на аналитичния вид на едноразрядния двоичен суматор. Непосредствена реализация на тези уравнения може да се постигне например с интегралните схеми 7453, 74H53, 7454, 74H54, 74S64, 74S65.

Следващият раздел е:

1.3 Многоразряден двоичен суматор с последователен пренос