I.3.
Многоразряден
двоичен
суматор с последователен
пренос
Тъй като
операция
събиране се
извършва поразрядно
и паралелно
във всички
разряди по
един и същи
начин, то
синтезът на
логическата
схема на един
многоразряден
суматор се
свежда до набиране
с помощта на
схемата на
едноразрядния
двоичен
суматор
(уравнения (2) и
(3)), на необходимата
дължина за
резултата.
Така например,
за събиране
на два
8-разрядни
операнда ще
трябва да се
реализира
8-разряден паралелен
суматор от 8
еднакви
едноразрядни
суматора,
които следва
да се свържат
помежду си
така, че
възникващите
в по-младшите
разряди
преноси да се
разпространяват
в по-старшите
разряди като
аргументи с
необходимата
логическа
стойност.
Това
включване води
до
логическата
схема от
фигура I.1,
която се нарича
суматор
с
последователен
пренос.
ЗАБЕЛЕЖКА:
Изчертаването
на схемата от
фигура I.1,
както и на
всички
останали
логически
схеми тук, е в
противоречие
с
изискванията
на БДС,
според който
не се допуска
разпространение
на
информация в
посоките отдясно
наляво и
отдолу
нагоре. "НАРУШЕНИЕТО"
на стандарта
е извършено от
нас умишлено
(единствено с
познавателна
цел с цел
постигане на
съответствие
с численото
изпълнение
на
операцията
при ръчното й
записване) !
Мотивът
за това се
съдържа в
ситуацията,
че само при
този начин на
изчертаване
на схемите, посоката
на
разпространяващите
се в схемата
на суматора
преноси,
съвпада с
тази при ръчно
изпълнение
на операция
събиране, където
преносите се
разпространяват
отдясно наляво,
т.е. в посока
към
по-старшите
разряди (според
правилата на
позиционните
бройни системи).
Така се
постига едно
естествено съответствие
между
работата на
схемата и ръчно
изпълняваната
в примерите
операция събиране.
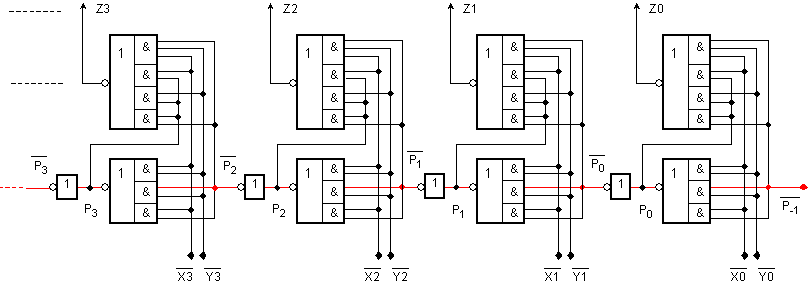
Фиг. I.1. Принципна
логическа
схема на 3
разряда от двоичен
комбинационен
суматор с
последователен
пренос
В
така
построената
схема (фигура
I.1)
сумата z се
получава
като
многоразрядно
двоично число
(например
8-битово):
![]()
когато на
нейните входове
се подават едновременно
във времето
цифрите на
операндите x
и y чрез
инверсните
си логически
стойности. Обикновено
получаването
на
инверсните
логически
стойности не
е проблем,
като се има предвид,
че тригерите,
изграждащи
регистрите,
от които се
снемат
операндите,
имат прав и
инверсен
изход, т.е.
всеки
логически
параметър се
съхранява
едновременно
с двете си
фази (права и
обратна). Не
бива да се
забравя, че
логическите стойности
на изходите
на суматора са
истинни само
докато на
входовете се
поддържат
истинните
стойности на
аргументите.
Всяко
изменение на
входа води до
ново събиране
и нова сума. В
този смисъл
суматорът събира
непрекъснато
във времето и
тази му функция
не може да
бъде
забранена!
Оценки
и изводи:
постигнатата
техническа
реализация
(фигура 1) на
синтезирания
суматор
(уравнения (2) и (3)),
както всяко
човешко
творение,
следва да бъде
подложено на
критичен
анализ и
оценка. Оценките,
които могат
да бъдат
давани, са два
вида - количествени
и качествени. Що се
отнася до
логическите
схеми, количествените
оценки, които
могат да
бъдат дадени,
най-често се
получават в
смисъла на критериите
"време
за
превключване"
- tΣ [s] и "обем
на
апаратните
разходи" - N [брой
NAND].
За
схемата от
фигура I.1, при n-разряден
суматор,
времето за
превключване
в най-тежкия
случай може
да бъде
оценено така
![]()
при
положение, че
се приеме
типично
време за
превключване
на един
инвертор
равно на t [s].
Това време се
формира в
най-дългата
верига от
последователно
превключващи
се инвертори,
а в случая
това е
веригата на
последователно
формиращите
се преноси.
Тази
най-тежка
ситуация възниква
само при
определени
операнди, например
при x=111...11 и y=000...01.
По втория
критерий
апаратните
разходи могат
да бъдат
оценени чрез
броя на
вложените
инвертори
(като
конструктивно
завършени
елементи) при
реализацията
на n-разрядния
суматор, а те
в случая са N=3.n на
брой.
Крайният
извод, който може
да бъде
направен
върху
получените
оценки е, че
получената
схема е
твърде бавна
и скъпа,
което я прави
практически
неприложима,
ето защо ще
се търсят
нови идеи и
подходи за
нейното
оптимизиране.
В този смисъл
схемата от
фигура I.1, като
първоначална
реализация,
представлява
само една
основа за
сравнение.
Следващият
раздел е:
1.4
Многоразряден
двоичен
суматор с ускорен
последователен
пренос