Последната редакция на тази книга е от 2021 година.

I.4. Многоразряден двоичен суматор с ускорен последователен пренос

Анализирайки схемата от фигура I.1 се вижда, че последователното включване на преносите от изход на вход налага включването на допълнителен инвертор. Това следва от факта, че функцията на преноса се получава с правата си стойност, а в уравнението на следващия пренос участвува като аргумент с инверсната си стойност (вижте уравнение (3)). Естествен е стремежът да се отстрани този последователен инвертор, с което би се повишило бързодействието на схемата. Реализацията на тази идея се изразява в последователното редуване на правите и инверсните стойности на функциите в отделните разряди както следва:

т.е. уравненията, по които се реализират суматорите в разрядите с четни номера са:

а в разрядите с нечетни номера са:

Логическата схема построена по тези две системи уравнения се нарича суматор с ускорен последователен пренос и има вида, показан на фигура I.2.

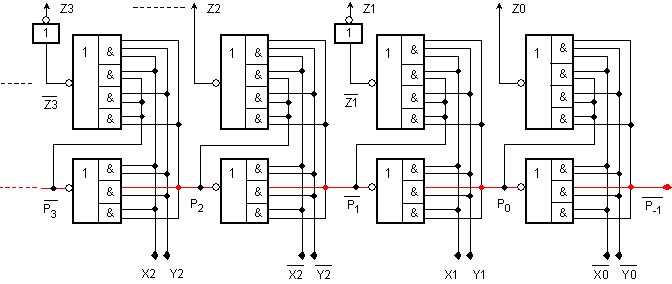
Фиг. I.2. Принципна логическа схема на суматор двоичен комбинационен с ускорен последователен пренос

Реализацията на горната схема може да бъде извършена с помощта на посочените вече в пункт I.2 интегрални схеми.

Оценки и изводи: лесно може да се пресметне, че при указаните в предидущата точка условия, времето за превключване на тази схема при четен брой разряди ще бъде

t_Σ=(n+2).t [s], а при нечетен брой - t_Σ=(n+1).t [s].

Двете схеми (фигура I.1 и фигура I.2) освен по бързодействие могат да се сравнят и по количеството инвертори, реализиращи една и съща дължина на суматора. Изводите, които могат да се направят от това сравнение са очевидни. Използуваната идея за синтез на този суматор е довела до двойно повишаване на бързодействието, т.е. чрез нея е получен ефект от 100%. Такова постижение е забележително и говори за ценността на идеята!

Следва да се отбележи и фактът, че в така получената схема (фигура I.2), цифрите на аргументите се подават с редуваща се права/инверсна стойност.

Синтезираният тук суматор е реализиран практически в интегралната схема 7480. Тя представлява пълен едноразряден двоичен комбинационен суматор. Схемата (представена на фигура I.3) има входове както за права (А1,А2; В1,В2), така и за инверсна стойност (А3,А4; В3,В4) на аргументите, а входът за пренос от по-младшия разряд е за права стойност (p_-1). В същото време изходът на преноса е инверсен not(p), а сумата (S) е изведена с двете си фази - права и инверсна. Това означава, че схемата е пряко подчинена на изложената по-горе идея за реализация на многоразрядния суматор.

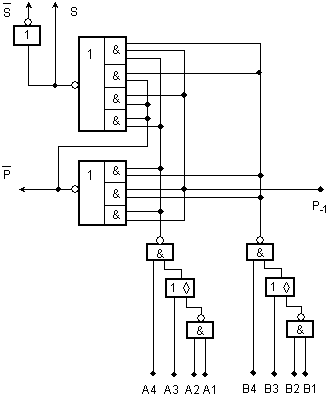
Фиг. I.3. Принципна логическа схема на ИС 7480

Онази част от електронната схема, която реализира изхода на функцията на преноса not(p), е реализирана чрез комплиментарна транзисторна двойка, с което се постига 10-кратно по-високо бързодействие на този изход. Това дава възможност тази интегрална схема да бъде комбинирана със схемата за паралелен пренос (вижте фигура I.9 в пункт I.7). Изводите А3 и В3 могат да се използват и като входове и като изходи. Когато се използват като изходи те реализират логическата функция от вида

но с малък коефициент на натоварване (максимум до 3).

Ако изводите А3, В3 се използват като входове, тогава на входовете А1, А2, съответно на В1, В2, трябва да се подава напрежение 0[v], т.е. логическа константа “0”. В случай, че входовете А1, А2, съответно В1, В2 се използват като такива, тогава изводите А3, съответно В3, трябва да бъдат свободни (т.е. не се препоръчва използването им).

Същата идея (за ускорен последователен пренос) е реализирана и в други интегрални схеми - например в схемата 7482, представляваща двуразряден двоичен суматор. В тази схема входът за пренос от по-младшия разряд е инверсен. Казаното се отнася и за ИС на 4-разрядния суматор 7483.

Въпроси и задачи:

1. Синтезирайте логическа схема, наричана полусуматор върху дефиниращата таблица от точка I.1. С получената схема реализирайте пълен едноразряден двоичен суматор.

2. С помощта на получената схема за полусуматор реализирайте многоразрядна броячна схема (комбинационен двоичен брояч с последователен пренос). Колко е времето за превключване на тази схема като функция от броя на разрядите?

3. Изчислете времето за превключване на 32-разряден суматор по указаните в точка I.3 и I.4 схеми, при типичните времена за превключване на схеми от фамилията 74xx и сравнете.

4. Реализирайте 16-разряден суматор чрез схемите 7480 и 7482. Сравнете бързодействието им.

5. Какви ще бъдат стойностите на функциите на сумата и преноса, ако в четните разряди се подадат правите стойности на аргументите, а в нечетните - инверсните (виж фиг. I.2)?

6. Изяснете процеса на превключване при събиране на 8-битовите числа:

X= 1 1 1 1 1 1 1 1 ,

Y= 1 1 1 1 1 1 1 1 .

Определете времето за превключване и постройте времедиаграма за рапространение на преносите. Направете същото за числата:

X= 1 1 1 1 1 1 1 1 ,

Y= 0 0 0 0 0 0 0 1

и сравнете с предидущия случай, като дадете обяснение за разликите, които сте установили.

Следващият раздел е:

1.5 Асинхронен двоичен суматор