Последната редакция на тази книга е от 2021 година.

I.5. Асинхронен двоичен суматор

Оценката на времето за превключване на суматорите, описани в точка I.3 и точка I.4 позволява да се определи максималната честота, с която може да се извършва операция събиране при синхронно управление. Смисълът на последното се състои в това, че към всяко следващо събиране може да се пристъпва след изчакване на максималното време за превключване на n-разрядния суматор. Максималното време за превключване е реално време за превключване само за определени операнди, предизвикващи възможно най-дългата верига за разпространение на преноса. Такива операнди се срещат рядко, което означава, че в повечето от случаите, сумата ще бъде готова много по-рано. Тогава логичен е въпросът - защо трябва да се изчаква, а не се фиксира резултатът още в момента в който е готов? Анализът на тази ситуация довежда до идеята за синтез на суматор, позволяващ прилагане в структури с асинхронно управление, което може да ускори операция събиране като цялостен алгоритъм. Ускоряването се реализира в смисъла на икономисаното време в следствие на по-ранното фиксиране на резултата (записване в регистър). При такова управление на операцията, колкото повече операции събиране изпълним, толкова икономисаното време ще бъде по-голямо. В този смисъл оценката на асинхронния суматор по бързодействие има статистически характер (например, като оценка може да се приеме средното време за извършване на 1000 събирания).

Реализацията на операция събиране в условията на асинхронно управление изисква изработването на логически сигнал за момента на поява на истинната сума, който е сигнал за фиксиране на резултата и сигнал за начало на ново събиране. С други думи, за да бъде фиксиран резултатът, някой трябва да съобщи, че той е готов.

Синтезът на този сигнал се търси в смисъла на следното твърдение: събирането на операндите е завършило, ако то е завършило в първия, във втория и в последния разряд. С други думи, сигналът "край на събирането" (КС) е една конюнкция от поразрядните сигнали за край на събирането, а указаният момент ще се маркира от неговия положителен фронт.

По аналогичен начин може да се определи и поразрядният сигнал за край на събирането, като неговият положителен фронт се търси чрез дизюнкцията на възникващия в разряда пренос, т.е.:

Предложеният израз (10), според алгебрата на логиката, е константа - логическа единица във всеки един момент от времето:

Тук обаче синтезът на тази функция се основава на практическото несъвършенство на електронните схеми, реализиращи логическите стойности, според които логическите стойности възникват в течение на времето, а не мигновено Тези практически "дефекти", както и паралелното изчисление на елементите на дизюнкцията (10) позволяват регистриране на смущение в тази константа във всеки момент, когато нейните елементи сменят стойността си. Графично тези смущения могат да се изразят както е показано на следната картинка:

.

След формиране от тези смущения на краткотрайна нула, става възможно реализирането на сигнала (9), като конюнкция от последователни във времето логически нули.

За да бъде отчетено реалното време за превключване на логическите елементи, които изчисляват стойността на преноса, поразрядните сигнали за край на събирането трябва да се формират от паралелно изчислени във времето логически стойности на функциите на преноса p_i и на неговата инверсия not(p_i). Паралелността може да се постигне само ако тези функции се изразят като функции от едни и същи аргументи. За целта в схемата на суматора с ускорен последователен пренос следва да се добавят липсващите логически функции, т.е. в четните разряди, където е реализирана функцията p_2i (вижте фигура I.2) ще се добави функцията на нейната инверсна фаза:

а в нечетните разряди – функцията на нейната права фаза:

Окончателният вид на сигнала "Край на събирането" е следния:

На фигура I.4 е представена принципната логическа схема на асинхронния двоичен комбинационен суматор с ускорен последователен пренос.

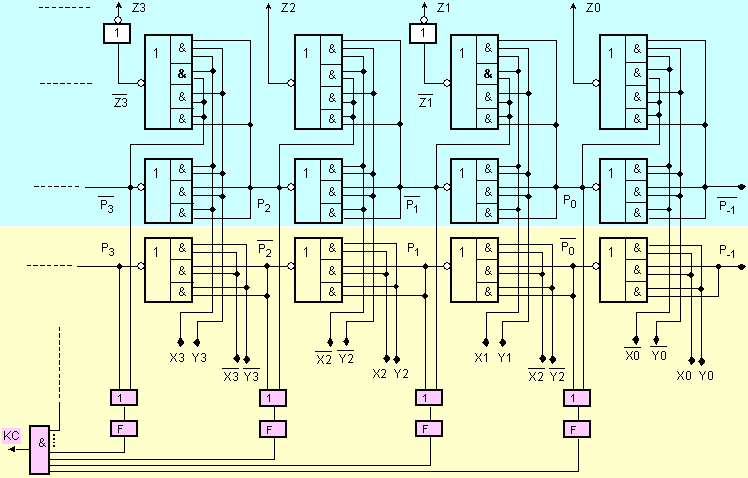
Фиг. I.4. Принципна логическа схема на асинхронен суматор

Елементите от фигура I.4, означени с буква F, имат за задача да удължат във времето появяващата се логическа нула на изхода на всяка схема ИЛИ така, че последователно следващите във времето нули (преноси) да се застъпват, което осигурява надеждното формиране на активната логическа стойност (нула) на сигнала КС на изхода на схемата И. Процесът на това формиране е показан на времедиаграмата от фигура I.5, където е изобразено как след появата на нови данни на входа на суматора (т.е. моментът, приеман за стартиране на операцията), се разпространяват преносите и се формират поразрядните сигнали КСi, как се формира тяхното разширение и резултатът - изходният сигнал КС. Продължителността на сигналите КСi е един фронт - t [s].

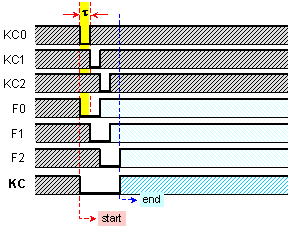
Фиг. I.5 Начало и край на събирането

Надеждното застъпване във времето на логическите нули от изходите на елементите F изисква разширението им отдясно с дължината поне на още един фронт, така че да бъде изпълнено отношението:

Именно при това отношение е построена времедиаграмата на фигура I.5.

Оценки и изводи: От фигура I.4 може да се получи оценката за апаратните разходи при реализиране на n-разряден суматор, а от фигура I.5 - оценката на времето за превключване на схемата. Последната е абсолютна или още фактическа и се отнася за събиране на конкретните операнди. Фактическото време за събиране на два конкретни операнда се определя от онази верижка от последователни преноси, която има най-голяма дължина. Както вече беше споменато, оценката за повишеното бързодействие следва да се получи в резултат на статистическо наблюдение на изпълнението на предварително определен брой събирания. За да бъде оценката обективна операндите при тези събирания следва да бъдат генерирани като случайни числа с равномерен закон на разпределение. Очевидният извод, който може да се направи е, че за възможността да събираме в режим на асинхронно управление, като отчитаме фактическата продължителност на операцията, сме заплатили с нарастване на апаратните разходи. Допълнителните апаратни разходи са изобразени в жълтата зона на схемата от фигура I.4 и както може да се съобрази, след сравняване на схемата с тази от фигура I.2, нарастването е с повече от 50%. В същото време суматорът е останал с последователен пренос и повишеното бързодействие не е абсолютно гарантирано, а има статистически смисъл. Читателят може да се запознае подробно с една конкретна реализация на метода за асинхронно управление в книга [3], точка 4.1.

Последното което остава да бъде изяснено в принципната схема на суматора е реализацията на елементите F. За сега тези елементи са употребени като “черни кутии”. За тях е определено, че те трябва да имат един вход и един изход, определена е тяхната функция, определена е и техническата стойност на тази функция (12). Изхождайки от тази информация следва да се синтезира логическата функция на този елемент.

Условието за паралелно изчисление на двете фази на функциите на преноса, формирането на тяхната дизюнкция и разширение е трудна за реализация задача, защото изисква специални решения на ниво електронни елементи. Тук ще представим едно решение, което може да облекчи тази реализация. Решението се основава на известна отстъпка от изявените по-горе разбирания. Тази отстъпка се изразява в това, че ние ще приемем изчислението на двете фази на функциите на преноса като последователно, с което значително ще облекчим логическата схема на суматора. В същото време, за да бъде възможен описаният вече ефект от тяхната дизюнкция, следва да засилим условието на разширението до следния му вид:

Последното условие може да бъде осигурено практически с помощта на значително задържане на сигнала на преноса във времето. Това най-лесно може да бъде постигнато чрез последователна верига от четен брой инвертори, т.е. със следната логическа функция:

В резултат на казаното, логическата схема, която ще реализира поразрядния сигнал КСi, ще има вида, показан на фигура I.6

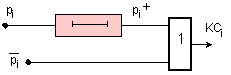
Фиг. I.6. Логическа схема за реализация на разширения поразряден сигнал

Превключването на логическите елементи от предложената схема е представено на фигура I.7. Логическата функция за край на събирането е реализирана по първоначалното уравнение (11). Вижда се, че активната стойност (нула) на тази функция се формира от застъпващите се във времето и последователно разпространяващи се сигнали КСi. Предният (положителният) фронт на сигнала КС отбелязва момента за край на операцията. Следващото събиране може да бъде стартирано веднага след запис на получената сума, т.е. някъде в сивата зона.

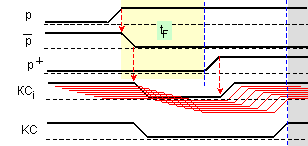
Фиг. I.7. Времедиаграма за формиране на сигнала КС

В резултат на изложеното принципната логическа схема на асинхронния суматор се променя и приема примерния вид от фигура I.8. Вижда се, че от първоналния вариант на схемата е премахната паралелната верига от логически елементи, изчисляващи противоположната фаза на получаваните преноси. Вместо нея са въведени последователни инвертори. Тъй като в суматора с ускорен последователен пренос фазите на преносите се редуват, то и схемите за реализация на функциите Ксi са различни и също се редуват. Читателят следва да обърне внимание на схемите в нечетните разряди (№1, 3, 5, ...) и да ги сравни с изобразената на фигура I.6.

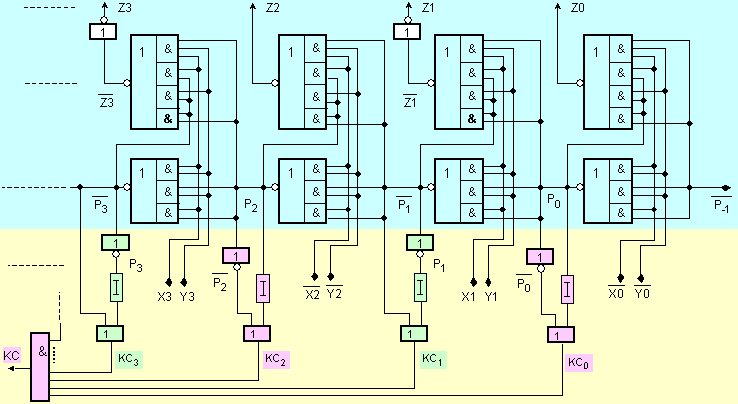
Фиг. I.8. Принципна логическа схема на асинхронен суматор (облекчена реализация)

Въпроси и задачи:

1. Получете обща количествена оценка на апаратните разходи в асинхронния суматор като функция от броя на разрядите и сравнете с предидущите оценки.

2. Постройте пълна времедиаграма за работата на 4-разряден двоичен суматор при събиране на числата: X=5 и Y=3; X=7 и Y=7; а също X=15 и Y=15.

3. Предложете икономична електронна или логическа схема за елемента F, реализираща разширението на логическото смущение.

4. Какво ще бъде времето за събиране, ако в пълната дължина на суматора възникнат няколко различни по дължина верижки от последователно разпространяващи се преноси?

Следващият раздел е:

1.6 Комбинационни двоични суматори с групов пренос