Последната редакция на тази книга е от 2021 година.

I.7. Комбинационен двоичен суматор с паралелен пренос

Кардиналното решение на проблема за повишаване на бързодействието на суматора се съдържа в отстраняване на функционалната зависимост на преноса от текущия разряд p_i от стойността на предидущия пренос p_i-1. Ето защо се търси възможност да се изрази преносът като функция само от операндите x, y.

Използувайки дефинираните в предидущия пункт означения при изразяване на преноса

за отделните разряди се получават следните уравнения:

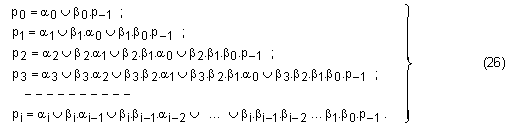
Получената система уравнения може да бъде преработена и записана още така

Реализацията на суматор с тази организация практически е неприемлива за големи дължини, поради значителната сложност на уравненията за логическите функциите на преносите, в разрядите с големи номера. Обикновено реализацията на паралелните преноси се осъществява само за група разряди (най-често с дължина 4[b]). С помощта на такива последователно свързани групи, се постига необходимата дължина на суматора. Суматор с такава групова организация се нарича суматор с паралелно-последователен пренос - последователен между групите и паралелен вътре във всяка група.

Ако се разгледа група от 4 разряда, то разпространяващите се в нея преноси са четири:

На най-младшия пренос p_-1 може да се гледа като на входен за групата пренос, а на най-старшия p₃, като на изходен от групата пренос.

Тогава, при условие, че на групата от 4 разряда се гледа като на една конструктивна единица, изходният пренос може да се запише по следния начин:

където:

При изказаното условие става възможно да се интерпретират елементите на получения запис аналогично на суматорите с групов пренос, т.е. изходният от групата пренос p₃, да се третира като междугрупов, функцията G - като местен групов, а функцията R - като условие за транзитен пренос. Тогава функцията на преноса, излизащ от всяка група може да се обобщи чрез името П:

където с буква j е означен номерът на групата.

Върху тази обобщена формула за последователния междугрупов пренос Пj отново може да се приложи подходът за изразяване на функцията на междугруповия пренос вече не като функция от предходния междугрупов пренос, а като функция от основните аргументи. Това води до системата:

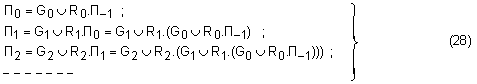
и т.н.

Тук отново може да се направи извод за нарастващата сложност на тези функции, чиято реализация би осигурила паралелното разпространение и на междугруповите преноси. След това отново би могло да се потърси приемлива дължина на група от групи, в която да се реализират практически горните уравнения. Става ясно, че от второто "ниво" на обединение на определени единици (дължини) в групи, същността на функцията на преноса се повтаря. Това означава, че ако дължините на всички конструкции (групи, групи от групи и т.н.) е една и съща, изграждането на схемата за паралелен пренос (между групите, между групите от групи и т.н.) може да се извърши чрез каскадно свързване на една универсална схема, реализираща едни и същи логически уравнения.Тази схема следва да реализира всички вътрешни за групата преноси по уравненията на горната система. Включването й ще бъде следното:

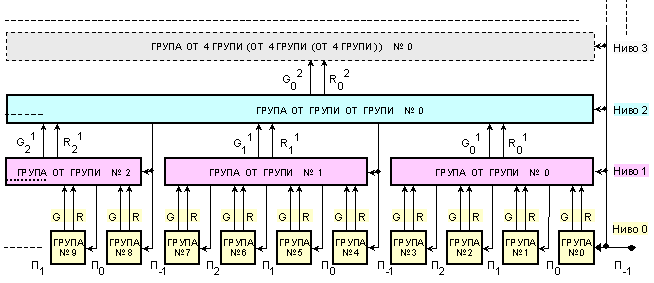
Фиг. I.8. Каскадно включване на схеми за ускорен пренос (нива 1, 2, 3, ...)

Освен всички вътрешни преноси, схемата формира и собствените си функции G и R, които не са функции на входния пренос и позволяват каскадното й свързване. Цялата тази идеология за йерархично изграждане на паралелния пренос намира практическо приложение в много интегрални схеми. Типичен пример е двойката 74181 и 74182, които съответно представляват 4-разряден двоичен суматор с паралелен пренос и схема за ускорен пренос.

Реализираните в схемата 74182 логически функции са в инверсна логика:

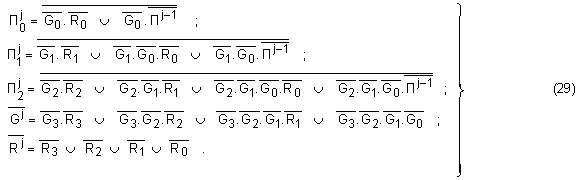
а самата схема има вида, показан на фигура I.9.

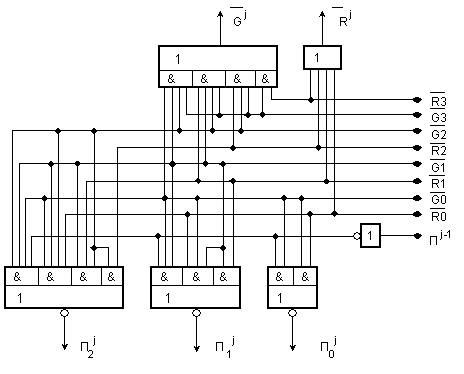
Фиг. I.9. Принципна логическа схема за 4-разряден ускорен (паралелен) пренос (ИС 74182)

Въпроси и задачи

1. Докажете правилността на уравненията от системата на схемата за ускорен пренос.

2. Постройте 32-разряден суматор с паралелно-последователен пренос чрез ИС 74181 и 74182, който да съдържа две групи от по 16 разряда.

3. Постройте 32-разряден суматор с паралелен пренос чрез същите схеми. Изчислете и сравнете времето им за превключване.

Следващият раздел е:

1.8 Многофункционална комбинационна схема (управляем суматор)